剑指Offer题解——随机刷题(三)
文章目录
- 剑指 Offer 60. n个骰子的点数
- 动态规划
- 剑指 Offer 61. 扑克牌中的顺子
- set集合
- 排序+遍历
- 剑指 Offer 62. 圆圈中最后剩下的数字
- 解法
- 剑指 Offer 64. 求1+2+…+n
- 递归
- 快速乘
- 剑指 Offer 65. 不用加减乘除做加法
- 位运算
- 剑指 Offer 66. 构建乘积数组
- 动态规划
- 推荐阅读
剑指 Offer 60. n个骰子的点数
剑指 Offer 60. n个骰子的点数
把n个骰子扔在地上,所有骰子朝上一面的点数之和为s。输入n,打印出s的所有可能的值出现的概率。
你需要用一个浮点数数组返回答案,其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。
示例 1:
输入: 1
输出: [0.16667,0.16667,0.16667,0.16667,0.16667,0.16667]
示例 2:
输入: 2
输出: [0.02778,0.05556,0.08333,0.11111,0.13889,0.16667,0.13889,0.11111,0.08333,0.05556,0.02778]
限制:
1 <= n <= 11
动态规划
我们可以把n个骰子的点数分解为n-1个骰子的点数加上一个骰子的点数。
根据1个骰子的点数概率数组求出2的点数概率数组,根据2的点数概率数组求出3的点数概率数组…直到求出n的点数。
class Solution {
public double[] twoSum(int n) {
double[] pre = {1/6d, 1/6d, 1/6d, 1/6d, 1/6d, 1/6d};
for (int i = 2; i <= n; i++) {
// n个骰子的点数和范围为[n,6n],所以共有6n-n+1=5n+1个值
double[] tmp = new double[5 * i + 1];
for (int j = 0; j < pre.length; j++) {
for (int k = 0; k < 6; k++) {
tmp[j + k] += pre[j] / 6;
}
}
pre = tmp;
}
return pre;
}
}
剑指 Offer 61. 扑克牌中的顺子
剑指 Offer 61. 扑克牌中的顺子
从扑克牌中随机抽5张牌,判断是不是一个顺子,即这5张牌是不是连续的。2~10为数字本身,A为1,J为11,Q为12,K为13,而大、小王为 0 ,可以看成任意数字。A 不能视为 14。
示例 1:
输入: [1,2,3,4,5]
输出: True
示例 2:
输入: [0,0,1,2,5]
输出: True
限制:
数组长度为 5
数组的数取值为 [0, 13] .
set集合
class Solution {
public boolean isStraight(int[] nums) {
Set<Integer> repeat = new HashSet<>();
int max = 0, min = 14;
for (int num : nums) {
// 跳过大小王
if (num == 0) {
continue;
}
max = Math.max(max, num);
min = Math.min(min, num);
// 若有重复,提前返回 false
if (repeat.contains(num)) {
return false;
}
repeat.add(num);
}
// 最大牌 - 最小牌 < 5 则可构成顺子
return max - min < 5;
}
}
排序+遍历
class Solution {
public boolean isStraight(int[] nums) {
int joker = 0;
Arrays.sort(nums);
for (int i = 0; i < 4; i++) {
if (nums[i] == 0) {
joker++;
} else if (nums[i] == nums[i + 1]){
return false;
}
}
return nums[4] - nums[joker] < 5;
}
}
剑指 Offer 62. 圆圈中最后剩下的数字
剑指 Offer 62. 圆圈中最后剩下的数字
0,1,n-1这n个数字排成一个圆圈,从数字0开始,每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。
例如,0、1、2、3、4这5个数字组成一个圆圈,从数字0开始每次删除第3个数字,则删除的前4个数字依次是2、0、4、1,因此最后剩下的数字是3。
示例 1:
输入: n = 5, m = 3
输出: 3
示例 2:
输入: n = 10, m = 17
输出: 2
限制:
1 <= n <= 10^5
1 <= m <= 10^6
解法
详解见leetcode
class Solution {
int recursion(int n, int m) {
if (n == 1) {
return 0;
}
int x = recursion(n - 1, m);
return (m + x) % n;
}
public int lastRemaining(int n, int m) {
return recursion(n, m);
}
}
剑指 Offer 64. 求1+2+…+n
剑指 Offer 64. 求1+2+…+n
求 1+2+…+n ,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。
示例 1:
输入: n = 3
输出: 6
示例 2:
输入: n = 9
输出: 45
限制:
1 <= n <= 10000
递归
class Solution {
public int sumNums(int n) {
return n == 0 ? 0 : n + sumNums(n - 1);
}
}
快速乘
违规用for训练,快速乘了解一下
class Solution {
public int sumNums(int n) {
// 1+2+...+n = (n * (n + 1)) / 2
return quickMulti(n, n + 1);
}
int quickMulti(int A, int B) {
int ans = 0;
// 计算 n * (n + 1)
for (; B != 0; B >>= 1) {
if ((B & 1) > 0) {
ans += A;
}
A <<= 1;
}
return ans / 2;
}
}
剑指 Offer 65. 不用加减乘除做加法
剑指 Offer 65. 不用加减乘除做加法
写一个函数,求两个整数之和,要求在函数体内不得使用 “+”、“-”、“*”、“/” 四则运算符号。
示例:
输入: a = 1, b = 1
输出: 2
提示:
a, b 均可能是负数或 0
结果不会溢出 32 位整数
位运算
class Solution {
public int add(int a, int b) {
// 当进位为 0 时跳出
while (b != 0) {
// c = 进位
int c = (a & b) << 1;
// a 为非进位和
a ^= b;
// b 为进位
b = c;
}
return a;
}
}
剑指 Offer 66. 构建乘积数组
剑指 Offer 66. 构建乘积数组
给定一个数组 A[0,1,…,n-1],请构建一个数组 B[0,1,…,n-1],其中 B 中的元素 B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1]。不能使用除法。
示例:
输入: [1,2,3,4,5]
输出: [120,60,40,30,24]
提示:
所有元素乘积之和不会溢出 32 位整数
a.length <= 100000
动态规划
根据题目对 B[i]B[i] 的定义,可列表格,如下图所示。
根据表格的主对角线(全为 11 ),可将表格分为 上三角 和 下三角 两部分。分别迭代计算下三角和上三角两部分的乘积,即可 不使用除法 就获得结果。
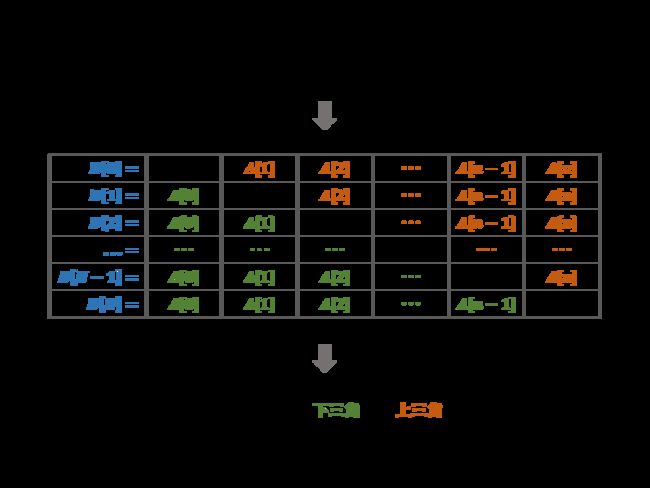
算法流程:
- 初始化:数组 B ,其中 B[0] = 1 ;辅助变量 tmp = 1;
- 计算 B[i] 的 下三角 各元素的乘积,直接乘入 B[i] ;
- 计算 B[i] 的 上三角 各元素的乘积,记为 tmp ,并乘入 B[i] ;
- 返回 B 。
class Solution {
public int[] constructArr(int[] a) {
if (a.length == 0) {
return new int[0];
}
int[] b = new int[a.length];
b[0] = 1;
int tmp = 1;
for (int i = 1; i < a.length; i++) {
b[i] = b[i - 1] * a[i - 1];
}
for (int i = a.length - 2; i >= 0; i--) {
tmp *= a[i + 1];
b[i] *= tmp;
}
return b;
}
}
推荐阅读
- 机器学习资料汇总
- 吴恩达《机器学习》视频、作业、源码
- 106页《Python进阶》中文版正式发布
- 李航《统计学习方法》第二版完整课件
- 机器学习数学全书,1900页PDF下载
![]()