二十四点游戏

一·题目要求
游戏规则：
从扑克中每次取出4张牌。使用加减乘除，第一个能得出24者为赢。（其中，J代表11，Q代表12，K代表13，A代表1）。
基本要求：
随机生成4个代表扑克牌牌面的数字字母，程序自动列出所有可能算出24的表达式，用擅长的语言（C/C++/Java或其他均可）实现程序解决问题。
1.程序风格良好(使用自定义注释模板)
2.列出表达式无重复。
二·题目分析
大概思路就是穷举4个数字排列组合后的所算式，选择其中结果为24的，并筛选符合数学法则的输出，让计算机算出所有与这4个数字相关的算式，选择其中得24的算输出即可。所以确定思路，穷举。大概分几个模块，主函数，转化四则运算的fun函数，for循环，if选择，scanf，printf。
三·调试
在将输入的值赋给num+i时，前面不能加入取地址符&，否则无法输出有效结果


四·测试
输入一组数据可以正常输出，但是有重复等式出现

五·编译结果
编译结果中的非法运算为不等于24的等式，其余有效等式为等于24的等式。


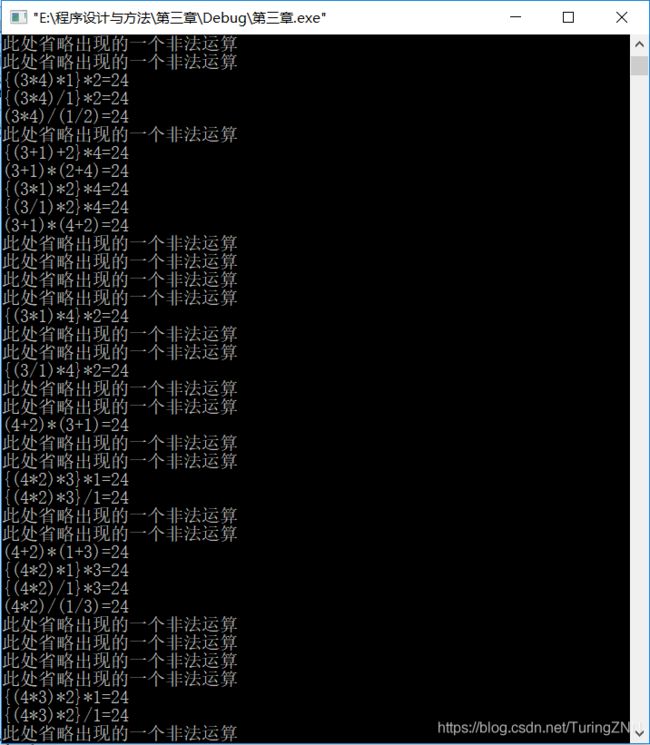
六·总结
通过这次学习，我学到了很多,这个程序不是很难，但是算法比较繁琐，要细心才行。通过此次程序设计,也让我们把平时学的理论知识用在了实际问题上,有助于我们的理解和运用,而且这个程序设计本身也比较有趣,能激发我们自己去深入研究。希望在以后的专业课学习中能够充分利用计算机本身速度快的优势,利用编写程序完成一些用手工计算很难完成的问题。

程序如下：

#include
//用switch语句将四则运算转化
double fun(double a1,double a2,int b)
{ switch(b)
{
case 0:return (a1+a2);
case 1:return (a1-a2);
case 2:return (a1*a2);
case 3:return (a1/a2);
}
}
void main()
{

int i,j,k,l,n,m,r,save[4];
double num[4]={1,1,1,1},tem1,tem2,tem3,abc=1111;
char sign[5]="+-*/";
//用for语句循环实现输入
printf("请输入4个数,数字与数字之间用空格隔开:");
for(i=0;i<4;i++)
{
scanf("%lf",num+i);
save[i]=num[i];
}
//用for和if语句实现数字的排列组合
for(i=0;i<4;i++)
for(j=0;j<4;j++)
if(j!=i)
{
for(k=0;k<4;k++)
if(k!=i&&k!=j)
{
for(l=0;l<4;l++)
if(l!=i&&l!=j&&l!=k)
{
//用两段语句分两种情况计算
for(n=0;n<4;n++)
for(m=0;m<4;m++)
for(r=0;r<4;r++)
{
tem1=fun(num[i],num[j],n);
tem2=fun(tem1,num[k],m);
tem3=fun(tem2,num[l],r);
//for循环实现运算的排列组合，上面是一种情况（不带有括号的）
//输出语句如下
if(tem3==24.0)printf("{(%d%c%d)%c%d}%c%d=24\n",save[i],sign[n],save[j],sign[m],save[k],sign[r],save[l]);
else
if(tem3==-24.0)printf("{%d%c(%d%c%d)}%c%d=24\n",save[k],sign[m],save[ i],sign[n],save[j],sign[r],save[l]);
else
if(tem3==1.0/24.0)printf("%d%c{(%d%c%d)%c%d}=24\n",save[l],sign[r],save[i],sign[n],save[j],sign[m],save[k]);
else
if(tem3==-1.0/24.0)printf("%d%c{%d%c(%d%c%d)}=24\n",save[l],sign[r],save[k],sign[n],save[i],sign[m],save[j]);
//下面是另一种
else
{
tem1=fun(num[i],num[j],n);
tem2=fun(num[k],num[l],r);
if(tem2 == 2 && m == 3)
printf("此处省略出现的一个非法运算\n");
//下面是两两组合的情况
else
{
tem3=fun(tem1,tem2,m);
if(tem3==24.0)
printf("(%d%c%d)%c(%d%c%d)=24\n",save[i],sign[n],save[j],sign[m], save[k],sign[r],save[l]);
}
}
}
}
}
}


}