近日复习概率论(mathematics for computer science)的时候读到了一个有趣的例子,在这里分享一下。都是一些非常简单好玩的概率知识,学数学的同学请绕道...勿喷。 ;)
这是一个平淡的星期天,你像往常一样在酒吧喝酒,顺便思考一下MMU分页机制的原理。
过了一会儿,一个彪形大汉坐到了你的旁边,点了几杯伏特加开始狂饮。正当你想到内核如何通过虚拟地址更改页目录和页表的时候,他开口了。
“小兄弟,玩骰子嘛?”
“不好意思,我不赌博。”
“嘿,我这可不是赌博,而且规则简单的很,要不要听听?”
你觉着反正也是闲着,就看看他葫芦里卖着什么药,于是说到:
“行,你说说是怎么个玩法?”
壮汉便从口袋里攥出三枚骰子,扔在桌子上:
“我这有三枚骰子,每一个都有6面,和普通骰子不一样的地方在于,每个相对面的点数是一样的,也就是说每个骰子只有三种点数,例如A骰子投出2、6、7的概率都是1/3. 咱们两每人下注100块,选一个骰子扔一下,谁点数小就输给对方,如何?”
发现骰子有些奇怪,你陷入了思索,B骰子有一个最大的点数9,而A骰子似乎有6和7这两个都不小的点数...
壮汉看出了你的怀疑,又说“小兄弟,这样,你先选骰子,我后选,这样如何?”
听起来不错。
”那我选B骰子“。随后壮汉拿起了A骰子。接下来就让我们分析一下你输掉的概率。
A vs B
首先我们找出所有的样本空间:
然后我们找到壮汉能够获胜的样本,一共有5个:
由于骰子上每一个点数出现的概率都是1/3,而且两个骰子是互相独立的,所以每一个样本出现的概率都是1/9. 如下图所示,你输掉的概率是5/9 :(
在你输掉100元后,壮汉将其归咎于你的坏运气,并劝你再来一盘。不过你现在只剩下打车的25块了,为了“帮助”你回本,壮汉提出,接下来这一盘你不用下注,如果你赢了就把刚刚赢的100块还给你,但要是输掉的话就欠他100块。考虑到刚刚已经吃了一个教训,这次应该能赢,你答应了他。
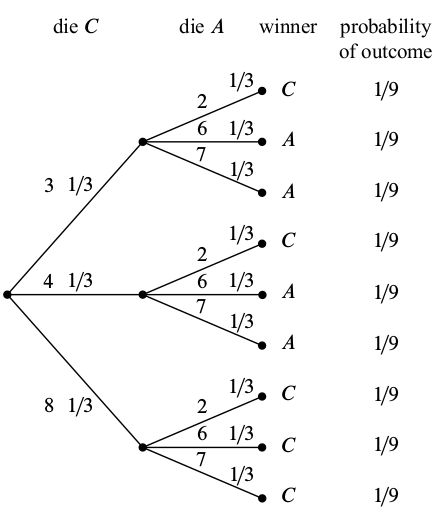
这次你选择A骰子,壮汉随后选择了C骰子。我们再来分析一下你输掉的概率。
C vs A
和上一盘一样,我们很容易就算出——你还是有5/9的概率输掉 :(
现在,你欠壮汉100块了,当你正考虑待会儿怎么跑掉时,壮汉”慈爱“答应再给你一次免下注的机会。
emmmm... A可以赢B,C可以赢A,那选C肯定没错了。于是你继续与壮汉展开斗争,这次,壮汉选择了B。
B vs C
和前两盘一样,我们可以很容易计算出结果——你还是5/9的概率输掉,又输了!
这怎么可能!A扔出的点数会比B更大,而C扔出的点数会比A更大,那C扔出的点数会什么会比B小呢??
这就是直觉带来的错误,在生活中很多东西满足传递性,很可惜,这里的概率不是。也就是说,只要你先选骰子,壮汉总是更可能赢!
于是,这一天你穿着内裤走回了家。
又是一个平淡的星期天,你穿着新买的衣服在酒吧休息,心想着下次再碰见壮汉一定要后扔骰子,把输掉的钱赢回来。果然,没过多久,壮汉出现了。
他听了你的要求,竟然欣然同意,但是建议这次玩大的——选完骰子后,每个人扔两次,把两次的点数之和作为输赢依据,每次下注200元。
emmmm... 扔两次,你想既然每一次扔骰子都更可能比壮汉大,扔两次更应该是这样了,于是便同意了。壮汉选择了B骰子,你知道A骰子比B骰子更可能扔出高点数,于是便选择的A骰子。
真的是这样吗?
Wrong!
Rolling Twice
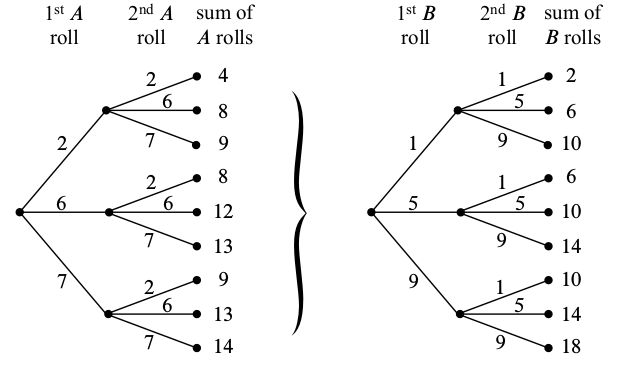
和前面的算法相同,由于每个人要扔两次骰子,总的样本数就是(3*3)*(3*3) = 91种,如下图所示:
可以看到,扔两次A骰子可能的样本为:
而扔两次B骰子可能的样本为:
所以A战胜B的总样本数为1+3+3+3+3+6+6+6+6 = 37个,而B战胜A的总样本数为42个(剩下的为平局)。即扔两次B更有可能获胜,和扔一次的情况矛盾!
看来,直觉又一次欺骗了我们,每一次扔出的点数都更可能高,但是两次扔的和却更可能低。事实上,在我们扔一个骰子比大小的时候,获胜的概率排序为 A > B > C > A, 而扔两个骰子的时候概率是反过来的,即A < B < C < A.
人们总是说“抢占先机”,但又说“后发优势”。从上面的例子也可以看出,先行动不一定就能占据优势,而后发也不一定就是好事,这正是统计学上的诠释。总之,在数据的概率上,不要相信生活经验/直觉,而是应该从数学的角度分析判断。另外,书上在讲条件概率的时候也提到了一个好玩的辛普森悖论, 感兴趣可看看。