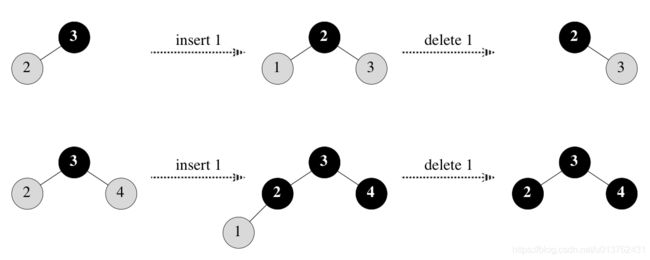
《算法导论》第三版第13章 红黑树 练习&思考题 个人答案

13.1 红黑树的性质

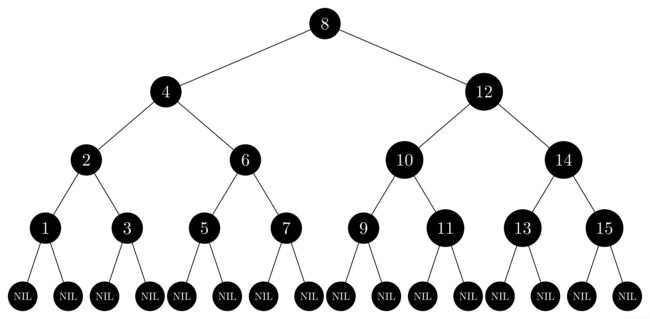
13.1-1

解：
完全二叉搜索树：

黑高为2的红黑树：

黑高为3的红黑树：

黑高为4的红黑树：

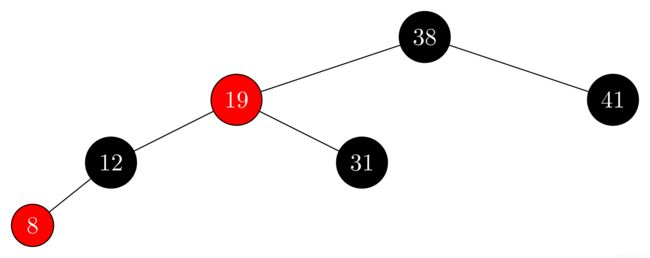
13.1-2

解：如果标红，不满足性质4，因为35是36的父结点，也是红色；如果标黑，不满足性质5，该条路径黑高超过其他路径。

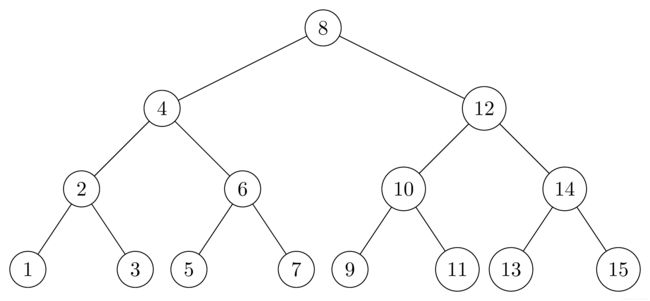
13.1-3

解：可以验证所得到的树仍然满足5个条件，所以是红黑树。

13.1-4

解：
（1）如果“吸收”前两个子结点都已经是黑色了，度为2；
（2）如果“吸收”前两个子结点一个是红一个是黑，度为3；
（3）如果“吸收”前两个子结点都是红色，度为4。
所得到的树，所有叶结点的深度相同。

13.1-5

证明：在最长的路径中，至少每个其他结点都是黑色的（一红一黑一红一黑）。在最短路径中，最多每个结点都是黑色的。由于两条路径包含相同数量的黑色结点，因此最长路径的长度最多为最短路径长度的两倍。

13.1-6

解：最多一层红一层黑，叶结点红，$2^{2k}-1$个；最少全黑，$2^k-1$个。

13.1-7

解：最大比值是2，每个黑色父结点有两个红色子结点；最小比值是0，全黑。

13.2 旋转

13.2-1

解：

RIGHT-ROTATE(T, x)
y = x.left
x.left = y.right
if y.right != T.nil
    y.right.p = x
y.p = x.p
if x.p == T.nil
    T.root = y
elseif x == x.p.right
    x.p.right = y
else x.p.left = y
y.right = x
x.p = y

13.2-2

证明：每个子结点都可以旋转到它的父结点上，只有根结点没法转。

13.2-3

解：a深度-1，b深度不变，c深度+1。

13.2-4

证明（机翻自参考答案）：Since the exercise asks about binary search trees rather than the more specific redblack trees, we assume here that leaves are full-fledged nodes, and we ignore the sentinels.
（由于练习要求二叉搜索树而不是更特殊的红黑树，我们假设叶子是完全成熟的节点而忽略了哨兵。）
Taking the book’s hint, we start by showing that with at most $n-1$ right rotations, we can convert any binary search tree into one that is just a right-going chain. The idea is simple. Let us define the right spine as the root and all descendants of the root that are reachable by following only right pointers from the root. A binary search tree that is just a right-going chain has all n nodes in the right spine.
（根据本书的提示，我们首先展示最多$n-1$次右旋，可以将任何二叉搜索树转换为一个单链。这个想法很简单。让我们将右脊定义为根，并且后继只能通过右指针到达。右向单链的二叉搜索树在右脊中具有所有n个结点。）
As long as the tree is not just a right spine, repeatedly find some node $y$ on the right spine that has a non-leaf left child $x$ and then perform a right rotation on $y$:
（只要树不仅仅是一个右脊，在右脊上重复找到一个节点$y$，其中有一个非叶左子结点$x$，然后在$y$上执行右旋：）

(In the above figure, note that any of $\alpha$, $\beta$, and $\gamma$ can be an empty subtree.) Observe that this right rotation adds $x$ to the right spine, and no other nodes leave the right spine. Thus, this right rotation increases the number of nodes in the right spine by $1$. Any binary search tree starts out with at least one node—the root—in the right spine. Moreover, if there are any nodes not on the right spine, then at least one such node has a parent on the right spine. Thus, at most $n-1$ right rotations are needed to put all nodes in the right spine, so that the tree consists of a single right-going chain.
（（在上图中，请注意$\alpha$，$\beta$和$\gamma$中的任何一个都可以是一个空子树。）观察到这个右旋将$x$添加到右脊，而没有其他节点离开右脊。因此，这种右旋使右脊中的节点数量增加$1$。任何二叉搜索树都从右脊以至少一个结点（根结点）开始。此外，如果有任何结点不在右脊上，则至少一个这样的结点在右脊上具有父节点。因此，将所有节点放在右脊柱中需要最多$n-1$次右旋，以使树由右向单链组成。）
If we knew the sequence of right rotations that transforms an arbitrary binary search tree $T$ to a single right-going chain $T^{\prime }$, then we could perform this sequence in reverse—turning each right rotation into its inverse left rotation—to transform $T^{\prime }$ back into $T$.
（如果我们知道将任意二叉搜索树$T$转换为单个右向链$T^{\prime }$的右旋序列，那么我们可以反向执行此序列，将每个右旋反向旋转到其反向左旋直到将$T^{\prime }$转换回$T$。）
Therefore, here is how we can transform any binary search tree $T_1$ into any other binary search tree $T_2$. Let $T^{\prime }$ be the unique right-going chain consisting of the nodes of $T_1$ (which is the same as the nodes of $T_2$). Let $r=⟨r_1,r_2,\dots ,r_k⟩$ be a sequence of right rotations that transforms $T_1$ to $T^{\prime }$, and let $r^{\prime }=⟨r_1^{\prime },r_2^{\prime },\dots ,r_{k^{\prime }}^{\prime }⟩$ be a sequence of right rotations that transforms $T_2$ to $T^{\prime }$. We know that there exist sequences $r$ and $r^{\prime }$ with $k$, $k^{\prime }\le n-1$. For each right rotation $r_i^{\prime }$, let $l_i^{\prime }$ be the corresponding inverse left rotation. Then the sequence $⟨r_1,r_2,\dots ,r_k,l_{k^{\prime }}^{\prime },l_{k^{\prime }-1}^{\prime },\dots ,l_2^{\prime },l_1^{\prime }⟩$ transforms $T_1$ to $T_2$ in at most $2n-2$ rotations.
（因此，以下是我们如何将任何二叉搜索树$T_1$转换为任何其他二叉搜索树$T_2$。 让$T^{\prime }$成为由$T_1$结点组成的唯一右链（与$T_2$的结点相同）。 设$r=⟨r_1，r_2，\dots ，r_k⟩$是一系列右旋，将$T_1$转换为$T^{\prime }$，让$r^{\prime }=⟨r_1^{\prime }，r_2^{\prime }，\dots ，r_{k^{\prime }}^{\prime }⟩$是一系列右旋，将$T_2$转换为$T^{\prime }$。 我们知道存在序列$r$和$r^{\prime }$和$k$，$k^{\prime }\le n-1$。 对于每个右旋$r_i^{\prime }$，让$l_i^{\prime }$为相应的反向左旋。 然后序列$⟨r_1，r_2，\dots ，r_k，l_{k^{\prime }}^{\prime }，l_{k^{\prime }-1}^{\prime }，\dots ，l_2^{\prime }，l_1^{\prime }⟩$将$T_1$转换为$T_2$ 最多$2n-2$次旋转。）

13.2-5

我们可以使用$O(n)$调用将$T_2$中的根节点旋转到$T_1$的根，然后分别在两个子树中使用相同的操作。共有$n$个结点，因此上限是$O(n^2)$。

13.3 插入

13.3-1

解：性质5会被破坏。

13.3-2

解：

13.3-3

解（来自参考答案）：
In Figure 13-5, nodes $A$, $B$, and $D$ have black-height $k+1$ in all cases, because each of their subtrees has black-height $k$ and a black root. Node $C$ has black-height $k+1$ on the left (because its red children have black-height $k+1$) and black-height $k+2$ on the right (because its black children have black-height $k+1$).

In Figure 13-6, nodes $A$, $B$, and $C$ have black-height $k+1$ in all cases. At left and in the middle, each of $A$'s and $B$'s subtrees has black-height $k$ and a black root, while $C$ has one such subtree and a red child with black-height $k+1$. At the right, each of $A$'s and $C$'s subtrees has black-height $k$ and a black root, while $B$'s red children each have black-height $k+1$.

Property 5 is preserved by the transformations. We have shown above that the black-height is well-defined within the subtrees pictured, so property 5 is preserved within those subtrees. Property 5 is preserved for the tree containing the subtrees pictured, because every path through these subtrees to a leaf contributes $k+2$ black nodes.

13.3-4

证明：只有在情况1或3会将某结点设为RED，在这两种情况下也只有z.p.p被标红。如果z.p.p是哨兵，z.p就是根结点。通过循环不变式的（b）和RB-INSERT-FIXUP的第1行，如果z.p是根，我们已经退出循环。唯一的细微之处在于情况2，我们在把 z.p.p标红之前设置z = z.p。因为我们在重新着色之前旋转，所以z.p.p的标识在情况2之前和之后是相同的，所以没有问题。

13.3-5

证明：
情况1：z和z.p.p是RED，如果循环终止，则z不能是root，因此修复后z是RED。
情况2：z和z.p是RED，旋转后z.p不能是root，因此修复后z.p是RED。
情况3：z是RED且z不能是root，因此修复后z是RED。
无论哪种情况都会有至少一个红结点。

13.3-6

解（翻译自参考答案）：
使用堆栈记录插入结点的路径，然后parent是堆栈中的顶部元素。
情况1：出栈$z.p$和$z.p.p$。
情况2：出栈$z.p$和$z.p.p$，然后入栈$z.p.p$和$z$。
情况3：出栈$z.p$，$z.p.p$和$z.p.p.p$，然后入栈$z.p$。

13.4 删除

13.4-1

情况1：转换为情况2，3，4
情况2：如果终止，子树的根结点（新的x）被设置为黑色。
情况3：转换为情况4。
情况4：根结点被设为黑色。

13.4-2

假设在$\text{RB-DELETE}$中$x$和$x.p$都是红色。这只可能在第9行的else情况下发生。由于是从红黑树中删除，因此在$\text{RB-TRANSPLANT}$第14行的调用中成为$x$兄弟的y.p的另一个孩子必须是黑色的，所以$x$是$x.p$唯一的孩子。 $\text{RB-DELETE-FIXUP}(T，x)$的while循环条件会立即被违反，所以只需设置$x.color=black$，恢复属性4。

13.4-3

13.4-4

由于$w$可能是$T.nil$，因此必须包含$\text{RB-DELETE-FIXUP}(T，x)$中检查或修改w的任何行。但是，如第185页所述，$w$永远不会是$T.nil$，因此不需要包含这些行。

13.4-5

（来自参考答案）
Our count will include the root (if it is black).
Case 1:
For each subtree, it is $2$ both before and after.
Case 2:
For $\alpha$ and $\beta$, it is $1+\text{count}(c)$ in both cases.
For the rest of the subtrees, it is from $2+\text{count}(c)$ to $1+\text{count}(c)$.
This decrease in the count for the other subtreese is handled by then having $x$ represent an additional black.
Case 3:
For $ϵ$ and $\zeta$, it is $2+\text{count}(c)$ both before and after.
For all the other subtrees, it is $1+\text{count}(c)$ both before and after.
Case 4:
For $\alpha$ and $\beta$, it is from $1+\text{count}(c)$ to $2+\text{count}(c)$.
For $\gamma$ and $\delta$, it is $1+\text{count}(c)+\text{count}(c^{\prime })$ both before and after.
For $ϵ$ and $\zeta$, it is $1+\text{count}(c)$ both before and after.
This increase in the count for $\alpha$ and $\beta$ is because $x$ before indicated an extra black.

13.4-6

仅当$x$的兄弟$w$为红色时才会出现情况1。如果$x.p$是红色的，那么连续会有两个红色，即$x.p$（也是$w.p$）和$w$，即使在调用$\text{RB-DELETE}$之前也会连续出现这两个红色。

13.4-7

不，红黑树不一定是一样的。 以下是两个示例：一个是树的形状发生变化，另一个是形状保持不变但节点颜色发生变化。

思考题

13-1（持久动态集合）

a.

b.

c.

d.

e.

13-2（红黑树上的连接操作）

a.

b.

c.

d.

e.

f.

13-3（AVL树）

a.

b.

c.

d.

13-4（treap树）

a.

b.

c.

d.

e.

f.

g.

h.

i.

j.