拓扑排序和关键路径算法 (C语言实现)
拓扑排序
首先要说明一下,拓扑排序不是一种排序方式,而是做一系列事件的可行次序。我们日常生活中,有时必须先完成一些事情,然后才能做另外一些事情。举个例子,我们学数学的时候,一定是先学习加减法,然后学乘除法,接着学习平方、根号等。不可能反着学。这就是拓扑排序。
拓扑排序可能是不唯一的,例如学完加减法之后,可以先学乘法,也可以先学除法。
拓扑排序不可能循环依赖 (存在环),例如在完成A事件之前必须完成B事件,在完成B事件之前必须完成A事件。如果发生这样的情况,那么这些事件不可能组成拓扑排序。如果在计算机运行的时候发生这样的情况,计算机就会被锁死。
好了,我们把这个问题抽象成“有向图”。对于有向图,只能输出最顶级的结点 (入度为0,没有上一级的顶点),输出后删除这个节点,一直循环,直到所有点都被输出,这就是一个拓扑排序。拓扑排序不可能存在环,因为环上的结点没有入度为0的点。
我们怎么计算一个有向图的拓扑排序呢?通过上述描述,其实已经很清楚了,步骤为:
1、找到有向图中的所有入度为0的结点;
2、输出入度为0的结点,同时把这些结点的下一级结点的入度 - 1。
3、重复2,直到所有点都输出。
4、判断是不是存在拓扑排序。如果输出的结点个数少于总结点数,则说明图中有环,这个图不含有拓扑排序。
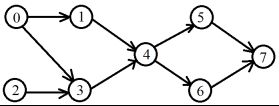
可以考虑用栈或队列辅助生成拓扑排序。用栈辅助生成拓扑排序时,左下图的输出结果为:2, 0, 1, 3, 4, 5, 6, 7。而用队列辅助生成拓扑排序时,左下图的输出结果为:0, 2, 1, 3, 4, 6, 5, 7。从这里我们也可以看出一个有向图可能存在多个拓扑排序。
我们先用数组实现的栈辅助生成拓扑排序:
step 1:找到有向图中的所有入度为0的结点:,并把编号存放在stack中
for(i = 0; i < size; i++)
{
struct LinkNode * node = arrNode[i].next;
struct ArrayNode myArrayNode = arrNode[i];
if(myArrayNode.inDegree == 0)
{
stack[top] = i; //把结点的编号存放到stack中
top++; //top + 1
}
}
step 2:输出入度为0的结点,同时把这些结点的下一级结点的入度 - 1。
top--; //top的位置没有内容,所以要先 - 1
index = stack[top]; //得到存放在stack中的编号
printf("%d -> ", index); //输出编号
count++; //计数 + 1
//从arrNode中获得结点的指针
struct LinkNode * node = (arrNode[index]).next;
//遍历
while(node != NULL) //如果子节点不是NULL就循环
{
int sonIndex = node->index; //子节点的index
//从arrNode中获得结点、结点信息
if(arrNode[sonIndex].inDegree > 0) //子节点的入度 > 0
{
//结点的inDegree - 1
arrNode[sonIndex].inDegree--;
//如果结点的inDegree == 0
if(arrNode[sonIndex].inDegree == 0)
{
//把结点的index (也就是sonIndex) 加入到stack中
stack[top] = sonIndex;
top++;
}
}
node = node->next;//指针指向下一个子节点
}
注意,要从arrNode中获得结点、结点信息,而不是从链表中获取结点信息。原因是如果有多个结点指向同一个结点,如果要从链表中获取结点信息,就需要 (多次) 更新结点信息,导致增加代码复杂度,同时影响效率。
step 3:循环step 2
step 4:判断是不是存在拓扑排序
if(count < size) //如果输出的结点数 < 总结点数
{
return 0; //不存在拓扑排序
}
return 1; //存在拓扑排序
完整的代码如下:
//用栈辅助实现的拓扑排序
#include 遍历邻接表的结果如下:其中3号结点的inDegree分别为1, 2, 2。所以如果读取链表中的结点的inDegree信息,结果就会出错。所以只从数组arrNode中读取结点的inDegree信息即可。运行结果如下:

如果在插入数据时加上这一行代码:addNode(5, 1); 有向图中就存在环,该有向图就不存在拓扑排序。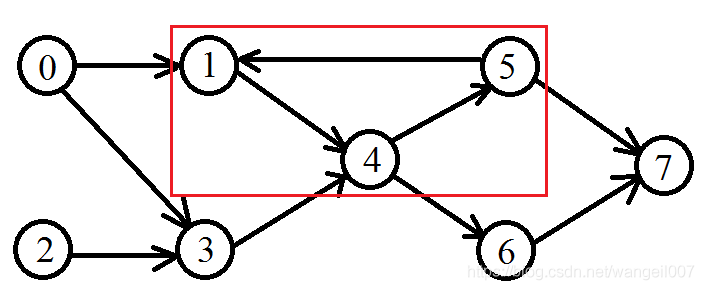
![]()
接下来,我们用数组实现的队列辅助生成拓扑排序:
step 1:找到有向图中的所有入度为0的结点
//1、遍历所有结点,寻找入度为0的结点,并把编号存放在queue中
for(i = 0; i < size; i++)
{
struct LinkNode * node = arrNode[i].next;
struct ArrayNode myArrayNode = arrNode[i];
if(myArrayNode.inDegree == 0)
{
queue[tail] = i; //队列是在尾部添加数据
tail++; //添加完数据后,tail++
}
}
step 2:输出入度为0的结点,同时把这些结点的下一级结点的入度 - 1
index = queue[head]; //获取队列的首元素
head++; //首元素出列
printf("%d -> ", index); //输出首元素
count++; //计数 + 1
//从arrNode中获得结点的指针
struct LinkNode * node = (arrNode[index]).next;
//遍历
while(node != NULL) //如果子节点不是NULL就循环
{
int sonIndex = node->index; //子节点的index
//从arrNode中获得结点、结点信息
if(arrNode[sonIndex].inDegree > 0) //子节点的入度 > 0
{
//node->inDegree--; //子节点的inDegree - 1
arrNode[sonIndex].inDegree--;
//如果结点的inDegree == 0
if(arrNode[sonIndex].inDegree == 0)
{
//把结点的index (也就是sonIndex) 加入到stack中
queue[tail] = sonIndex;
tail++; //队列的尾巴 + 1
}
}
node = node->next;//变成子节点
}
step 3:循环step 2
step 4:判断是不是存在拓扑排序 (与用stack实现拓扑排序相同,略)
完整的代码如下:
#include
#include
int size = 8;
//声明结构体
struct LinkNode{
int index; //编号
struct LinkNode * next; //下一个结点的指针
};
struct ArrayNode{
int inDegree; //入度
struct LinkNode * next; //指向链表的指针
};
int queue [100]; //用队列辅助实现拓扑排序,用数组实现队列
int head = 0;//队列的head的index
int tail = 0;//队列的tail的index
//用一个数组存放首元素。每个首元素后面用指针连接各个结点
struct ArrayNode arrNode[8];
//头插法添加数据,得到的结果的次序是反的
void addNode(int parentIndex, int nodeIndex)
{
//同上
}
int TopologicalOrderByQueue() //队列辅助实现的拓扑排序
{
int count = 0;//用来计数
int index = 0;//输出的结点的编号
int i = 0; //循环变量
//1、遍历所有结点,寻找入度为0的结点,并把编号存放在queue中
for(i = 0; i < size; i++)
{
struct LinkNode * node = arrNode[i].next;
struct ArrayNode myArrayNode = arrNode[i];
if(myArrayNode.inDegree == 0)
{
queue[tail] = i; //队列是在尾部添加数据
tail++; //添加完数据后,tail++
}
}
//2、弹出栈中的结点,输出结点编号。同时让该结点的下一级结点的入度 - 1
//3、循环,直到栈中的结点为0,即top == 0
while(head < tail)
{
index = queue[head]; //获取队列的首元素
head++; //首元素出列
printf("%d -> ", index); //输出首元素
count++; //计数 + 1
//从arrNode中获得结点的指针
struct LinkNode * node = (arrNode[index]).next;
//遍历
while(node != NULL) //如果子节点不是NULL就循环
{
int sonIndex = node->index; //子节点的index
//从arrNode中获得结点、结点信息
if(arrNode[sonIndex].inDegree > 0) //子节点的入度 > 0
{
//node->inDegree--; //子节点的inDegree - 1
arrNode[sonIndex].inDegree--;
//如果结点的inDegree == 0
if(arrNode[sonIndex].inDegree == 0)
{
//把结点的index (也就是sonIndex) 加入到stack中
queue[tail] = sonIndex;
tail++; //队列的尾巴 + 1
}
}
node = node->next;//变成子节点
}
}
if(count < size) //如果输出的结点数 < 总结点数
{
return 0; //不存在拓扑排序
}
return 1; //存在拓扑排序
}
void releaseResource() //释放资源
{
//同前
}
int main()
{
//同前
}
运行结果如下:
![]()
如果在插入数据时加上这一行代码:addNode(5, 1); 有向图中就存在环,该有向图就不存在拓扑排序。
![]()
拓扑排序的时间复杂度为O(N + M)。N是顶点个数,M是弧 (有向图中的边) 的数量。
下一节,我们将实现关键路径的算法。