MPC实现自动驾驶轨迹跟踪

本文继MPC运动学方法实现轨迹跟踪推导进行matlab代码实现，虽然你们找到的参考书都是simulink carsim联仿，我却坚持使用纯代码仿真，因为牛逼。
代码模板沿用了LQR轨迹跟踪算法Python/Matlab算法实现，LQR轨迹跟踪算法Python/Matlab算法实现2, LQR轨迹跟踪算法Python算法实现3。代码直接复制下来就能用，拿去爽。

clc
clear all

Kp = 1.0 ; 
dt = 0.1  ;% [s]
Length = 2.9 ;% [m] wheel base of vehicle
Nx=3;%状态量的个数
Nu =2;%控制量的个数
Np =60;%预测步长
Nc=30;%控制步长
Row=10;%松弛因子
Q=100*eye(Nx*Np,Nx*Np);    
R=1*eye(Nc*Nu);
    
max_steer =60 * pi/180; % in rad
target_v =30.0 / 3.6;

cx = 0:0.1:200; % sampling interception from 0 to 100, with step 0.1
for i = 1:500% here we create a original reference line, which the vehicle should always follow when there is no obstacles;
    cy(i) = -sin(cx(i)/10)*cx(i)/8;
end
for i = 501: length(cx)
    cy(i) = -sin(cx(i)/10)*cx(i)/8; %cy(500);
end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% here we provide another reference line for testing, now you dont need to
% use it
% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

p = [cx', cy'];
 %计算一阶导数
 for i = 1:length(cx)-1
 pd(i) = (p(i+1,2)-p(i,2))/(p(i+1,1)-p(i,1));
 end
 pd(end+1) = pd(end);
  %计算二阶导数
 for i =2: length(cx)-1
     pdd(i) = (p(i+1,2)-2*p(i,2) + p(i-1,2))/(0.5*(-p(i-1,1)+p(i+1,1)))^2;
 end
      pdd(1) = pdd(2);
     pdd(length(cx)) = pdd(length(cx)-1);
    %计算曲率 
  for i  = 1:length(cx)-1
     k(i) = (pdd(i))/(1+pd(i)^2)^(1.5);
  end
  
  cx= cx';
  cy =cy';
  cyaw = atan(pd');
  ck = k';
%%%%%%%%%%%%%%%%%%%%   above things are preprocessing   %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

i = 1;
T = 80;
lastIndex = length(cx);
x = 0.1; y = -0.1; yaw = 0.1; v = 0.1;
U = [0.01;0.01];
vd1_p = 0;
vd2_p = 0;
vd_p = [vd1_p; vd2_p];
ind =0;
figure
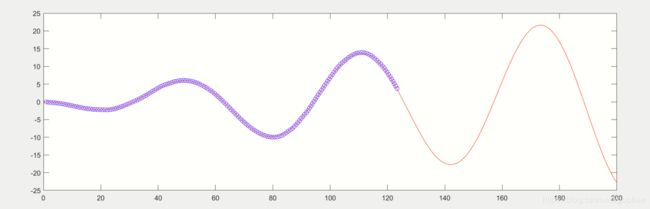
     plot(cx,cy,'r-')
     hold on
     
while ind < length(cx)
   
  [delta,v,ind,e,U, vd_p ] = mpc_control(x,y,yaw,cx,cy,cyaw,ck,dt,Length,Q,R,U,target_v,vd_p) ;
   
    if abs(e)> 3% we do not allow the vehicle deviation larger than 4
        fprintf('diviation too big!\n')
        break;
    end
    delta
     [x,y,yaw,v] = update(x,y,yaw,v, delta, dt,Length, max_steer); %update the vehicle state for next iteration
     posx(i) = x;
     posy(i)  =y;
     i = i+1;

     plot(posx(i-1),posy(i-1),'bo')
     pause(0.01);
     
      hold on
end

%% supplimented functions are as follows:
% function"Update" updates vehicle states
function [x, y, yaw, v] = update(x, y, yaw, v, delta,dt,Length,max_steer)% update x, y, yaw, and velocity
 delta = max(min(max_steer, delta), -max_steer);
    x = x + v * cos(yaw) * dt + randn(1)* 0;
    y = y + v * sin(yaw) * dt +  randn(1)* 0;
    yaw = yaw + v / Length * tan(delta) * dt ;
   v = v ;
end

function [a] = PIDcontrol(target_v, current_v, Kp) %we originally control v separately
a = Kp * (target_v - current_v);
end

function [angle] = pipi(angle) % the unit of angle is in rad, but in this case, you dont need to use it ;

if (angle > pi)
    angle =  angle - 2*pi;
elseif (angle < -pi)
    angle = angle + 2*pi;
else
    angle = angle;
end
end


function    [delta,v,ind,e,U, vd_p ] = ...
    mpc_control(x,y,yaw,cx,cy,cyaw,ck,dt,Length,Q,R,U,target_v,vd_p) 

u = [x,y,yaw];
[ind, e] = calc_target_index(x,y,cx,cy,cyaw); % find current vehicle location, it is represented by reference index
vd1=target_v ;
k =ck(ind);
vd2=atan(Length * k);

r = [cx(ind), cy(ind), cyaw(ind)];
    Nx=3;%状态量的个数
    Nu =2;%控制量的个数
    Np =60;%预测步长
    Nc=30;%控制步长
    Row=10;%松弛因子
    t_d =u(3);%角度为弧度
    
    kesi=zeros(Nx+Nu,1);
    kesi(1)=u(1)-r(1);%u(1)==X(1)
    kesi(2)=u(2)-r(2);%u(2)==X(2)
    kesi(3)=t_d-r(3); %u(3)==X(3)
    kesi(4)=U(1);
    kesi(5)=U(2);
%     fprintf('Update start, u(1)=%4.2f\n',U(1))
%     fprintf('Update start, u(2)=%4.2f\n',U(2))
    T=dt;
    % Mobile Robot Parameters
    L = Length;
    % Mobile Robot variable
    
%矩阵初始化   
    delta_u=zeros(Nx,Nu);
    
    a=[1    0   -vd1*sin(t_d)*T;
       0    1   vd1*cos(t_d)*T;
       0    0   1;];
    b=[cos(t_d)*T   0;
       sin(t_d)*T   0;
       tan(vd2)*T/L      vd1*T/(L * (cos(vd2)^2))];
    A_cell=cell(2,2);
    B_cell=cell(2,1);
    A_cell{1,1}=a;
    A_cell{1,2}=b;
    A_cell{2,1}=zeros(Nu,Nx);
    A_cell{2,2}=eye(Nu);
    B_cell{1,1}=b;
    B_cell{2,1}=eye(Nu);
    A=cell2mat(A_cell);
    B=cell2mat(B_cell);
    C=[1 0 0 0 0;0 1 0 0 0;0 0 1 0 0;];
    PHI_cell=cell(Np,1);
    THETA_cell=cell(Np,Nc);
    for j=1:1:Np
        PHI_cell{j,1}=C*A^j;
        for k=1:1:Nc
            if k<=j
                THETA_cell{j,k}=C*A^(j-k)*B;
            else 
                THETA_cell{j,k}=zeros(Nx,Nu);
            end
        end
    end
    PHI=cell2mat(PHI_cell);%size(PHI)=[Nx*Np Nx+Nu]
    THETA=cell2mat(THETA_cell);%size(THETA)=[Nx*Np Nu*(Nc+1)]
    H_cell=cell(2,2);
    H_cell{1,1}=THETA'*Q*THETA+R;
    H_cell{1,2}=zeros(Nu*Nc,1);
    H_cell{2,1}=zeros(1,Nu*Nc);
    H_cell{2,2}=Row;
    H=cell2mat(H_cell);
    H = 1/2*(H+ H');
     error=PHI*kesi;
    f_cell=cell(1,2);
    f_cell{1,1}=2*error'*Q*THETA;
    f_cell{1,2}=0;
%     f=(cell2mat(f_cell))';
    f=cell2mat(f_cell);
    
 %% 以下为约束生成区域
 %不等式约束
    A_t=zeros(Nc,Nc);%见falcone论文 P181
    for p=1:1:Nc
        for q=1:1:Nc
            if q<=p 
                A_t(p,q)=1;
            else 
                A_t(p,q)=0;
            end
        end 
    end 
    A_I=kron(A_t,eye(Nu));%对应于falcone论文约束处理的矩阵A,求克罗内克积
    Ut=kron(ones(Nc,1),U);%此处感觉论文里的克罗内科积有问题,暂时交换顺序
    umin=[-0.2;-0.54;];%维数与控制变量的个数相同
    umax=[0.2;0.332];
%     delta_umin=[0.05;-0.0082;];
%     delta_umax=[0.05;0.0082];
        delta_umin = [ -2.2 ; -0.64];
    delta_umax = [  0.2 ;  0.64];
    Umin=kron(ones(Nc,1),umin);
    Umax=kron(ones(Nc,1),umax);
    A_cons_cell={A_I zeros(Nu*Nc,1);-A_I zeros(Nu*Nc,1)};
    b_cons_cell={Umax-Ut;-Umin+Ut};
    A_cons=cell2mat(A_cons_cell);%（求解方程）状态量不等式约束增益矩阵，转换为绝对值的取值范围
    b_cons=cell2mat(b_cons_cell);%（求解方程）状态量不等式约束的取值
   % 状态量约束
    M=10; 
    delta_Umin=kron(ones(Nc,1),delta_umin);
    delta_Umax=kron(ones(Nc,1),delta_umax);
    lb=[delta_Umin;0];%（求解方程）状态量下界，包含控制时域内控制增量和松弛因子
    ub=[delta_Umax;M];%（求解方程）状态量上界，包含控制时域内控制增量和松弛因子

    %% 开始求解过程
%     options = optimset('Algorithm','interior-point-convex');
    options = optimoptions('quadprog','Display','iter','MaxIterations',100,'TolFun',1e-16);
    %options = optimset('Algorithm','interior-point-convex'); 
    [X,fval,exitflag]=quadprog(H,f,A_cons,b_cons,[],[],lb,ub,[],options);
    %% 计算输出
%     for i = 1:length(X)
%     if X == [] 
%         delta_u(1)=randn(1)*0.01;
%         delta_u(2)=randn(1)*0.01;
%     elseif  X(i) == 0
%         delta_u(1)=randn(1)*0.01;
%         delta_u(2)=randn(1)*0.01;
%     else
%         delta_u(1)=X(1);
%         delta_u(2)=X(2);
%     end
%     end
        delta_u(1)=X(1);
        delta_u(2)=X(2);
        
    U(1)=kesi(4)+delta_u(1) ;%用于存储上一个时刻的控制量
    U(2)=kesi(5)+delta_u(2); %kesi here is previous step U
    u_real(1)=U(1)+vd1; %  vd1 and vd2 here is U_ref
    u_real(2)=U(2)+vd2;
   delta=  u_real(2);
    v = u_real(1);
%     U(1)=kesi(4)+delta_u(1) + vd1 - vd_p(1);%用于存储上一个时刻的控制量
%     U(2)=kesi(5)+delta_u(2) + vd2 - vd_p(2); %kesi here is previous step U

    kesi(4) = U(1);
    kesi(5) = U(2);
    vd_p  = [vd1;vd2 ]; 
%     delta =  U(2)
%     v = 3

end

function [ind, error] = calc_target_index(x,y, cx,cy,cyaw)% find my location, and lateral error
N =  length(cx);
Distance = zeros(N,1);
for i = 1:N
Distance(i) =  sqrt((cx(i)-x)^2 + (cy(i)-y)^2);
end
[value, location]= min(Distance);
ind = location

dx1 =  cx(ind) - x;
dy1 =  cy(ind) - y ;
angle = pipi(cyaw(ind)-atan(dy1/dx1));
heading = cyaw(ind)*180/pi
    if y<cy(ind) 
        error = -value;
    else
        error = value;
    end
% error = value;
end

效果如图：