深度学习与PyTorch笔记23
小技巧
动量 momentum
惯性
定义
无动量梯度更新的公式: w k + 1 = w k − α ∇ f ( w k ) w^{k+1}=w^{k}-\alpha\nabla f(w^{k}) wk+1=wk−α∇f(wk)
有动量梯度更新公式: w k + 1 = w k − α z k + 1 w^{k+1}=w^{k}-\alpha z^{k+1} wk+1=wk−αzk+1
z k + 1 = β z k − ∇ f ( w k ) z^{k+1}=\beta z^{k}-\nabla f(w^{k}) zk+1=βzk−∇f(wk)
w k + 1 = w k − α ∇ f ( w k ) − α β z k w^{k+1}=w^{k}-\alpha\nabla f(w^{k})-\alpha\beta z^{k} wk+1=wk−α∇f(wk)−αβzk
当 w k w^{k} wk减去一个梯度的时候就意味着他是朝着那个梯度移动的,原来的 w ′ w^{'} w′的更新方向是朝着 ∇ w k \nabla_{w}^{k} ∇wk梯度的方向,现在的还多了一个新的方向 z k z^{k} zk。这个 z k z^{k} zk是某一种迭代的算子,他代表的是上一次梯度的方向 ∇ w k − 1 \nabla_{w}^{k-1} ∇wk−1。 β \beta β参数的不同选择会产生不同的效益。
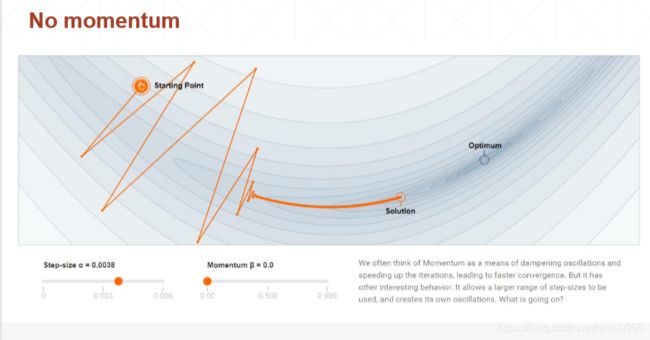
1找不到全局最优解2刚开始更新方向很随机,不规则,尖锐

取0.78,考虑历史方向多一些,在刚开始的时候更新的会比较缓和。当添加一个动量时,当参数选择好的话,局部最小值解更接近全局最小值。
在PyTorch中调用momentum
optimizer = torch.optim.SGD(model.parameters(),args.lr,
momentum=args.momentum,
weight_decay=args.weight_decay)
有一些优化器,比如Adam,中是没有momentum参数的,因为其本身就利用了momentum做了一些优化,不需要额外管理momentum,只有最原始的SGD需要额外的设置此参数。
学习率衰减 learning rate decay
learning rate产生的影响

太小,更新时间长
太大,会出现假梯度离散或者忽大忽小,不收敛,找不到最合适的解
怎么选择learning rate:刚开始选择一个稍微大一些的,比如0.1,然后随着training再慢慢衰减至0.0001。动态learning rate的好处是,在达不到好的状态时,他的锐减会瞬间提升性能。
两种比较常见的learning rate decay的方案
一、当loss下降到一定时间一直不动时
CLASS torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer,mode='min',factor=10,
verbose=False,threshold=0.0001,threshold_mode='rel',cooldown=0,min_lr=0,epps=1e-08)
scheduler = ReduceLROnPlateau(optimizer,'min')
for epoch in xange(args.start_epoch,args.epochs):
train(train_loader, model, criterion, optimizer, epoch)
result_avg, loss_val = validata(val_loader, model, criterion, epoch)
scheduler.step(loss_val) #每调用一次监听一次loss,饱和就把lr减去一半或者按照一定规则衰减,若不饱和则无作用,仅记录
二、规定每20K个epoch把learning rate衰减一下
# Assuming optimizer uses lr = 0.05 for all groups
# lr = 0.05 if epoch < 30
# lr = 0.005 if 30 <=epoch < 60
# lr = 0.0005 if 60 <=epoch < 90
# ...
scheduler = StepLR(optimizer,step_size=30,gamma=0.1)
for epoch in range(100):
scheduler.step()
train(...)
validate(...)
一般step_size会设置为1k或者10k。
Early Stopping

可以理解为是检测overfitting的一种情况,也可以理解为是early stopping。
How-To
- Validation set to select parameters利用Validation set来做一个模型参数的选择
- Monitor validation performance检测performance
- Stop at the highest val perf.提前在最高点停止(连续下滑一段时间后认为出现最高点)
Dropout
学习的时候不需要学习全部的w参数,要求有效的w越小越好,不是范数趋近于0而是connection趋近于0。
- Learning less to learn better
- Each connnection has p=[0,1] to lose
在pytorch中加dropout
net_dropped = torch.nn.Sequential(
torch.nn.Linear(784,200),
torch.nn.Dropout(0.5), # drop 50% of the neuron
torch.nn.ReLU(),
torch.nn.Linear(200,200),
torch.nn.Dropout(0.5), # drop 50% of the neuron
torch.nn.ReLU(),
torch.nn.Linear(200,10),
)
可以在任意层加入dropout层
clarification
- torch.nn.Dropout(p=dropout_prob)当p=1时代表可能会全断,当p=0.1时代表断的概率比较小
- tf.nn.dropout(keep_prob)当p=1时意味着所有的连接都保持住,当p=0.1时代表断掉的概率比较大
dropout的行为在train和test中是不一样的,在train中有dropout,但在test中是没有dropout这一行为的,为了防止在validation的时候还使用train的行为必须人为的把行为切换到evaluation中去,如果不切换的话会发现还是有0.5的概率被dropout,performance会下降一点。
for epoch in range(epochs):
# train
net_dropped.train()
for batch_idx,(data,target) in enumerate(train_loader):
...
net_dropped.eval()
test_loss = 0
correct = 0
for data,target in test_loader:
...
Stochastic Gradient Descent
- Stochastic
- not random!
- 符合一个分布,不是真正的均匀分布,有一定的随机性,不是随机给一个数。 x → f ( x ) ∼ N ( 0 , x ) x\to f(x)\sim N(0,x) x→f(x)∼N(0,x)
- Deterministic
- 输入输出一一对应 x → f ( x ) x\to f(x) x→f(x)
把整个数据集上所有梯度的均值变成在batch上面所有均值的梯度。
- ∂ ∂ θ j J ( θ ) = 1 m ∑ i = 1 m ( y ^ i − y i ) x j i \frac{\partial}{\partial\theta_{j}}J(\theta)=\frac{1}{m}\sum_{i=1}^{m}(\widehat{y}^{i}-y^{i})x^{i}_{j} ∂θj∂J(θ)=m1i=1∑m(y i−yi)xji
- Vanilla (Batch) GD θ j = θ j − α ∂ ∂ θ j J ( θ ) \theta_{j}=\theta_{j}-\alpha\frac{\partial}{\partial\theta_{j}}J(\theta) θj=θj−α∂θj∂J(θ)
- 节省显存 Stochastic GD f o r i i n r a n g e ( m ) : θ j = θ j − α ( y ^ i − y i ) x j i ∇ J ∇ θ j for\quad i\quad in\quad range(m):\\\theta_{j}=\theta_{j}-\alpha(\widehat{y}^{i}-y^{i})x^{i}_{j}\frac{\nabla J}{\nabla \theta_{j}} foriinrange(m):θj=θj−α(y i−yi)xji∇θj∇J这里 ( y ^ i − y i ) x j i (\widehat{y}^{i}-y^{i})x^{i}_{j} (y i−yi)xji is only one example.