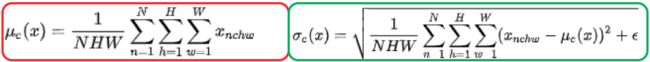Normalization那些事

Normalization methods

            

• FeatMaps：可以直观理解为一摞书[由N本书摞起来得到，每本书有C页，每页有H行字，每行字有W个字符]！

Batch-Norm

• 直观理解：BN-mean的形状为[1 x C x 1 x 1]， 其中BN-mean[1, i, 1, 1]表示将这摞书每一本的第 i 页取出来合成一个由C页组成的序号为i-th的书，然后求该书的“平均字”，BN-var同理！
• 计算公式：

                         

• 适用场景：占显存相对较小[意味着batchsize可以取大一些]的任务【图像分类、视频理解、目标检测等任务】！
• Pytorch：

import torch
from torch import nn
bn = nn.BatchNorm2d(num_features=3, eps=0, affine=False, track_running_stats=False)
x = torch.rand(10, 3, 5, 5)*10000 
official_bn = bn(x)
x1 = x.permute(1,0,2,3).view(3, -1)
mu  = x1.mean(dim=1).view(1,3,1,1)
std = x1.std(dim=1, unbiased=False).view(1,3,1,1)
self_bn = (x - mu) / std
diff = (official_bn - self_bn).sum()
print('diff={}'.format(diff)) 

Layer-Norm

• 直观理解：LN-mean的形状为[N x 1 x 1 x 1]， 其中LN-mean[n, 1, 1, 1]表示将这摞书中第 n 本书的平均字，LN-var同理！
• 计算公式：

                               

• 适用场景：数据长度[channel]可变的RNN系列模型，对显卡资源要求低【不受batchsize的影响】！
• Pytorch：

import torch
from torch import nn

x = torch.rand(10, 3, 5, 5)*10000
# eps=0 排除干扰
# elementwise_affine=False 不作映射
# 这里的映射和 BN 以及下文的 IN 有区别，它是 elementwise 的 affine，
# 即 gamma 和 beta 不是 channel 维的向量，而是维度等于 normalized_shape 的矩阵
ln = nn.LayerNorm(normalized_shape=[3, 5, 5], eps=0, elementwise_affine=False)
official_ln = ln(x)
x1 = x.view(10, -1)
mu = x1.mean(dim=1).view(10, 1, 1, 1)
std = x1.std(dim=1, unbiased=False).view(10, 1, 1, 1)
self_ln = (x - mu) / std
diff = (self_ln - official_ln).sum()
print('diff={}'.format(diff))

Instance-Norm

• 直观理解：IN-mean的形状为[N x C x 1 x 1]， 其中IN-mean[n, c, 1, 1]表示将第 n 本书第c页的平均字，IN-var同理！
• 计算公式：

                             

• 适用场景：生成模型、Style-Transfer ！【单个sample内进行，不依赖batchsize】
• Pytorch：

import torch
from torch import nn

x = torch.rand(10, 3, 5, 5) * 10000
# gamma, beta : [1, num_channels, 1, 1]
In = nn.InstanceNorm2d(num_features=3, eps=0, affine=False, track_running_stats=False)
official_in = In(x)
x1 = x.view(30, -1)
mu = x1.mean(dim=1).view(10, 3, 1, 1)
std = x1.std(dim=1, unbiased=False).view(10, 3, 1, 1)
self_in = (x - mu) / std
diff = (self_in - official_in).sum()
print('diff={}'.format(diff)) 

Group-Norm

• 直观理解：GN-mean的形状为[N x (C/G) x 1 x 1]， 将每本书以G页为单位，划分为C/G个小册子，则GN-mean[n, c, 1, 1]表示第n本书的第c个小册子的均值，GN-var同理！
• 计算公式：

                

• 适用场景：适用于占用显存比较大的任务，例如图像分割!
• Pytorch：

import torch
from torch import nn

x = torch.rand(10, 20, 5, 5)*10000
# gamma, beta : [1, num_channels, 1, 1]
gn = nn.GroupNorm(num_groups=4, num_channels=20, eps=0, affine=False)
official_gn = gn(x)
x1 = x.view(10, 4, -1)
mu = x1.mean(dim=-1).reshape(10, 4, -1)
std = x1.std(dim=-1).reshape(10, 4, -1)
x1_norm = (x1 - mu) / std
self_gn = x1_norm.reshape(10, 20, 5, 5)
diff = (self_gn - official_gn).sum()
print('diff={}'.format(diff)) 

Reference

1. Group Normalization[2017-ECCV]
2. Instance Normalization:The Missing Ingredient for Fast Stylization[2016-arXiv]
3. https://www.zhihu.com/search?q=instance%20normalization&utm_content=search_suggestion&type=content