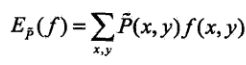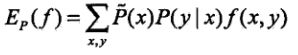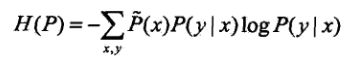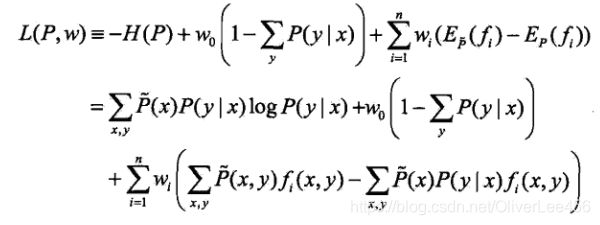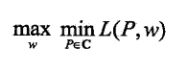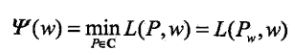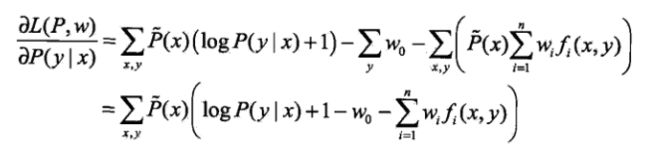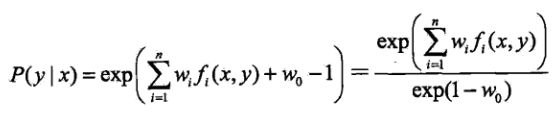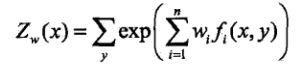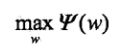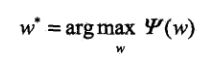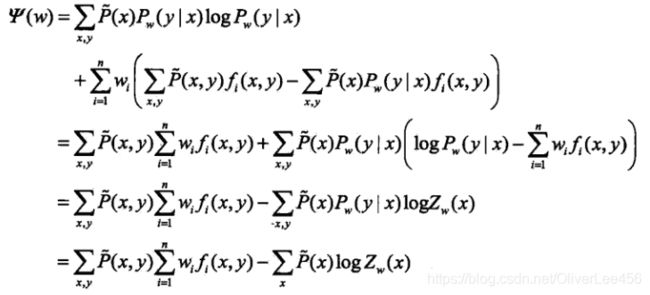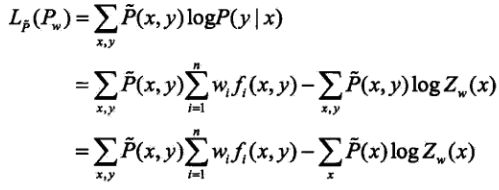逻辑回归与最大熵模型_统计学习方法_学习笔记
- 前言
逻辑回归（Logistic Regression）是一个老生常谈的分类算法，谈得越多也就越具有代表性，因为其背后蕴含着深刻的建模思想。
关于逻辑回归的一种理解思路在我的斯坦福CS229的第一篇笔记--线性回归中已经做了介绍。这种思路从广义线性模型（GLM）的角度出发进行理解：二分类问题的逻辑回归，是在假设先验分布p（y）为伯努利分布情况下（由于伯努利分布属于指数分布族），根据GLM规则对后验分布p（y|x）进行建模的结果。
在此章内容中，我想从另外两个角度加深对逻辑回归的理解。第一个角度从公式本身出发；第二个角度则从最大熵模型出发。
目录
1 从公式本身出发
2 最大熵模型
2.1 最大熵原理
2.2 最大熵模型的构建
2.3 最大熵模型的学习
2.4 对偶函数的极大化与极大似然法
2.5 最大熵模型与逻辑回归
3 小结
1 从公式本身出发
为了方便讨论，以下都以二分类（假设正类别为1，负类别为0）逻辑回归进行叙述。
在线性回归中，我们期待用一个线性函数去拟合数据，因此对p（y|x）直接建模为
，利用梯度下降法或者正规方程求解得到参数w，也就得到了我们建模的结果。但是如果我们仍然想利用线性函数对于分类问题进行建模（留意到概率取值区间 [0,1]），就必须将预测的p（y=1|x）的结果进行非线性映射到区间 [0,1]，逻辑回归选择的非线性映射函数为sigmoid函数，函数表达式如下：
sigmoid函数图像如下所示：
那么通过该映射函数，便可将结果映射到区间 [0,1]。因此一个样本属于正类别的概率便可写作如下形式。这里为了书写方便，将偏置向量合并入w之中。
（1.1）
该值表示的是分为正类别的概率。值越大，越相信其属于正类别；越小，越相信其属于负类别。由于sigmoid函数中心对称，因此可以中间值0.5作为一个临界点：当概率大于0.5时，认为其的类别为正类别；反之则认为其属于负类别。
以上是我们对于逻辑分布的直观认识，接下来为了加深理解，引入几率（odds）这个概念。
一个事件的几率是指该事件发生的概率与不发生的概率的比值。即如果事件发生的概率是p，那么该事件发生的几率是 
。那么该事件发生的对数几率（这也被称为logit函数）为：
（1.2）
那么不妨算下公式（1.1）的对数几率，也就是一个样本为正类别的概率的logit函数形式是怎么样。将（1.1）带入（1.2）可得：
（1.3）
这个结果会让人恍然明白：逻辑回归的建模基础为：假设，新样本分为正类别的概率的对数几率（或logit函数）是输入数据x的线性函数。因此从这个假设前提出发理解逻辑回归，顺水推舟，你也就不会疑惑为什么这个非线性函数要选择sigmoid形式而不是其他形式了。因为在此假设前提上，你可以假设p（y=1|x）结果未知，利用（1.3）式直接求解p（y=1|x），会发现结果即为sigmoid函数。可能会问：为什么要做那么拗口的假设，可能冥冥之中自有天意吧。若哪位大佬理解了，请不吝赐教。
理解了上式，也就理解了逻辑回归这个名称的由来：逻辑（Logistic）二字由logit函数而来；逻辑回归的本质其实是以回归的手段去解决分类问题，因为其回归的是输入数据的线性函数的logit函数（对数几率）。
2 最大熵模型
这一节阐述最大熵原理、利用最大熵原理构建最大熵模型、以及最大熵模型与逻辑回归的关系。
2.1 最大熵原理
关于熵的概念，在前一章决策树的特征选择一节已经进行叙述，这里不再赘述。
最大熵原理是在选择模型中采用的一种策略。最大熵原理认为，学习概率模型时，在所有可能的概率模型（分布）中，熵最大的模型是最好的模型。若在模型选择时具有一些约束条件，那么在满足约束条件的情况下，熵最大的模型即为最好的模型。
沿用上章对于熵的记号，我们可知熵的取值范围如下所示。当X服从于均匀分布时，熵取最大值。
即最大熵原理认为，在满足实际情况的条件下（约束条件），熵越大的模型是越好的模型，因此选择熵最大的模型作为选择模型。因此我们可以得到一个结论便是，在约束条件下，均匀分布的模型是最优模型。
2.2 最大熵模型的构建
利用最大熵原理来解决分类问题所构建的模型称为最大熵模型。接下来阐述最大熵模型的构建过程。
在分类问题中，我们建立的模型为条件概率模型
，假设给定训练数据集：
学习的目标是得到熵最大的模型。接下来进行一些定义。
首先根据训练数据，我们可以得到联合分布
的经验联合分布
，以及边缘分布
经验边缘分布
。其中N为样本容量，而v为计数器（确保理解经验分布与真实分布）。
用一个特征函数f（x，y）描述输入x和输出y之间的某一个事实。即每一个特征函数代表着每一个约束条件。其定义如下所示：
特征函数f（x，y）关于经验联合分布的期望值，用
表示：
特征函数f（x，y）关于模型真实分布与经验边缘分布的期望值，用
表示：
如果模型能够获取训练数据中的信息，即有
，那么就认为这个模型是有意义的。这也是我们进行模型选择时最基本的约束，即我们选择的模型应该尽可能的贴合真实分布。
那么假设满足上述所有约束的条件的模型集合为：
定义在条件概率分布上的条件熵为：
那么根据最大熵的思想，我们选择的应是其中条件熵最大的模型。即选择的模型P为：
2.3 最大熵模型的学习
有了最大熵模型的形式，那么最大熵模型的学习便是求解得到熵最大的那个模型的过程。这其实就是一个优化问题。与支持向量机类似，这里会遇到原始问题转为对偶问题的求解策略进行求解。若对于对偶问题忘记了，可以查阅该书的附录或者参照我的斯坦福CS229-支持向量机的笔记。
因此由2.2节的讨论，可将优化问题写作如下形式：
按照最优化问题的习惯，将求最大值问题改写为等价的求最小值问题：
接下来又到了求解优化问题的过程了，耐心推导每一步，收获一定很大。
首先，我们有n+1个约束条件，引入拉格朗日乘子
，定义拉格朗日函数
：
由此，写出要优化的原始问题：
将原始问题转为对偶问题：
由于拉格朗日函数关于P为凸函数，因为其原始问题的解和对偶问题的解是一样的，所以可以将其转换为对偶问题进行求解。首先解决其内部的极小化问题，将其记作：
其中 称为对偶函数，将其解即为如下形式：
对偶函数是w的函数，要求解的表达式，通过对P求偏导，令其为0，即可解决。具体如下：
令该偏导为0，得到：
（2.1）
由于 
，因此可将（2.1）进行改写，从而抵消掉一个参数
：
具体地，将公式（2.1）两端对y求和：
从而可以得到右边第一项的表达式：
（2.2）
由公式（2.2），令：
（2.3）
将公式（2.3）带入（2.1），得到最优解
的表达式如下：
（2.4）
由此，对偶函数的表达式即可确定。接下来，便是求解对偶问题外部最大值了：
将其解记为
，即：
由此，便完成了最大熵模型的构建和学习的过程了。你可能有疑惑，模型不是还剩最后一步，即求解对偶函数的最大值还没有阐述。实际上，可以将求解对偶函数的极大值转为最大熵模型的极大似然估计进行解决。这也是下一小节的内容。
2.4 对偶函数的极大化与极大似然法
下面将要证明对偶函数的极大化与最大熵模型的极大似然估计等价。
（1）先看对偶函数：
将最优解表达式带入，得到对偶函数的表达式并化解，如下所示：
（2.5）
由倒数第二行到倒数第一行的推导用到了 这个条件。
（2）再看最大熵模型的极大似然估计：
由于已知训练数据的经验概率分布，那么可以写出条件概率分布的对数似然函数：
（2.6）
对于书中的上式，我是存在疑惑的，因为我觉得该式少了一个系数N（样本数量），即应该为如下形式：
有没有这个N，对于最后的估计结果没有影响，所以就不深入了。
同样将最优解带入（2.6），得：
（2.7）
（2.5）与（2.7）是相等的。因此验证了结论：对偶函数的极大化与最大熵模型的极大似然估计等价。所以我们在求解对偶函数的极大值时，可以将其转换为最大熵模型的极大似然估计进行求解。
2.5 最大熵模型与逻辑回归
由此我们得到了最大熵模型的构建与学习过程。那么其与逻辑回归的关系如何呢？
在回头看一眼（2.4），如下所示：
对比二分类逻辑回归：
不明显的话，再看看多分类逻辑回归，其中k代表类别：
这其实就很明显了，逻辑回归应用的思想就是最大熵的思想。最大熵模型是逻辑回归模型的更一般的表现形式。
写到这里，不禁感叹：科学真的是有共性的，这些背后的大一统的科学究竟是什么？
3 小结
本章的主要内容在于最大熵模型的构建与学习，核心在于理解最大熵的原理。看完本章，至少我们可以从三个角度对逻辑回归进行理解：
（1）从广义线性模型（GLM）角度出发，以二分类逻辑回归为例：二分类问题的逻辑回归，是在假设先验分布p（y）为伯努利分布情况下（由于伯努利分布属于指数分布族），根据GLM规则对后验分布p（y|x）进行建模的结果。
（2）从对数几率的角度出发，逻辑回归的建模基础为：假设新样本分为正类别的概率的对数几率（或logit函数）是输入数据x的线性函数。（这一角度和GLM感觉有点类似）
（3）从最大熵模型的角度，最大熵模型是逻辑回归的一般形式，逻辑回归是最大熵模型的一个代表。
三种不同角度都不约而同指向了逻辑回归。最开始接触逻辑回归时觉得其很是别扭，现在深感存在即合理。
书中的第三小节介绍了可用于最大熵模型参数的学习算法：改进的迭代尺度法与拟牛顿法。这里不再赘述。