KD树

简介

一种基于欧氏距离的K维点集的组织方式，可以用于搜索K维点对的最大距离，极限搜索时间复杂度为$O(k{N}^{1-\frac{1}{k}})$

构建

与二叉搜索树大致类似，一般使用的方法是轮流以每个维度作为标准（普通的二叉搜索树只有一维，标准不变）。

以下图中的二维空间为例，第一次以$x=7$为标准，左边部分以$y=4$为标准，左上方以$x=4$为标准。

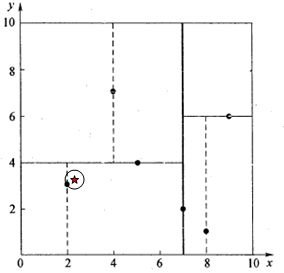
选择的值约莫一半即可，即隔开的两个空间中的点数一半一半即可。

搜索

首先当然是往指定维度的方向搜索了，上图中的搜索路径为$(7,2)(5,4)(2,3)$。但是这样并不一定找到最优解。

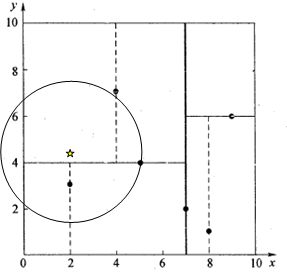
譬如此案例，打星号的点虽然在$y=4$的上方，但是与之最近的点却在下方。那么什么时候需要找另外一边呢？

显然，上图中，因为查询上方后得到的最优距离为半径所画的圆越过分界线，所以不清楚下方是否还有更优解（在此圆中）。如果上方画出来的圆不能越过，当然就不会有更优解。

模板

HDU4347 - The Closeset M Points

找出最近的$m$个点

double精度可能不够

#include
using namespace std;
const int N=55555,K=5;
const int inf=0x3f3f3f3f;
const long double eps=1e-14;
#define ls (rt<<1)
#define rs (rt<<1|1)

#define sqr(x) (x)*(x)
int k,n,idx;   //k为维数,n为点数
struct point {
    int x[K];
    bool operator < (const point &u) const {
        return x[idx]<u.x[idx];
    }
} po[N];

typedef pair<long double,point>tp;
priority_queue<tp>Q;// m个内部，距离较大放队首，要弹出

struct kdTree {
    point pt[N<<2];
    int son[N<<2];

    void build(int l,int r,int rt=1,int dep=0) {
        if(l>r)
            return;
        son[rt]=r-l;
        son[ls]=son[rs]=-1;
        idx=dep%k;
        int mid=(l+r)/2;
        // 第idx维作为标准隔开
        nth_element(po+l,po+mid,po+r+1);
        pt[rt]=po[mid];
        build(l,mid-1,ls,dep+1);
        build(mid+1,r,rs,dep+1);
    }
    void query(point p,int m,int rt=1,int dep=0) {
        if(son[rt]==-1)
            return;
        tp nd(0,pt[rt]);// 距离
        for(int i=0; i<k; i++)
            nd.first+=sqr((long double)(nd.second.x[i]-p.x[i]));
        int dim=dep%k,x=ls,y=rs,fg=0;
        if(p.x[dim]>=pt[rt].x[dim])
            swap(x,y);
        // 查询对应的半空间
        if(~son[x])
            query(p,m,x,dep+1);
        // 入队列，以距离作为第一关键字
        
        if(Q.size()<m)
            Q.push(nd),fg=1;// 还不够m，往另外一边找
        else {
            if(nd.first<Q.top().first)
                Q.pop(),Q.push(nd);
            
            if(sqr((long double)(p.x[dim]-pt[rt].x[dim]))<Q.top().first)
                fg=1; // 画的圈越过分界线，避免开根号所有距离都平分了
        }
        if(~son[y]&&fg)
            query(p,m,y,dep+1);
    }
} kd;
void print(point &p) {
    for(int j=0; j<k; j++)
        printf("%d%c",p.x[j],j==k-1?'\n':' ');
}
int main() {
    while(scanf("%d%d",&n,&k)!=EOF) {
        while(!Q.empty())Q.pop();
        for(int i=1; i<=n; i++)
            for(int j=0; j<k; j++)
                scanf("%d",&po[i].x[j]);
        kd.build(1,n);
        int t,m;
        for(scanf("%d",&t); t--;) {
            point ask;
            for(int j=0; j<k; j++)
                scanf("%d",&ask.x[j]);
            scanf("%d",&m);
            kd.query(ask,m);
            printf("the closest %d points are:\n", m);
            point pt[20];
            for(int j=0; !Q.empty(); j++)
                pt[j]=Q.top().second,Q.pop();
            for(int j=m-1; j>=0; j--)
                print(pt[j]);
        }
    }
    return 0;
}