强化学习 入门（一）

1. 强化学习 是什么

强化学习，Reinforcement Learning，RL。

虽然我们不知道人类学习的终极奥秘，但有一些事情是可以理解的：我们首先需要与环境进行交互，无论是人们学习驾驶汽车还是婴儿学习走路，学习都是基于和环境的相互交互。

从互动中学习的思想就是强化学习，它是一种基于环境相互交互的学习算法。

2. 强化学习 的问题

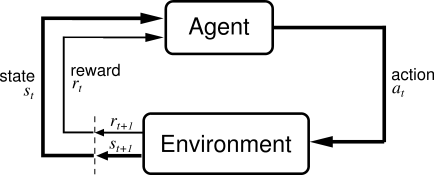
下图所示是一个强化学习过程。

上图中，Agent 是一个小个体（比如你是一个学生个体），Environment 是大环境，个体难以改变只能适应的对象（比如期末考试）。

学生(Agent) 发出 action（行为，比如考试前的拖延症）应对考试(Environment)，之后考试(Environment) 会反馈一个 state（结果状态，比如考试前拖延会导致考前焦虑），完成考试(Environment) 任务最后会给学生(Agent) 一个 reward（奖励，比如考试成绩）。

最经典的是 【小孩学走路问题】：
小孩是一个试图通过采取行动（走路）来操纵环境（在地上走路）的个体，它试图从一个状态（它走的每一步）转移到另一个状态。当它完成任务的一个子模块（孩子走了几步）时，孩子会获得奖励（比如一些巧克力），但是当它不会走路时，就不会收到任何巧克力（负反馈过程）。

3. 强化学习 vs 机器学习

• 监督学习：数据集包含 label，输入和输出之间都存在映射。强化学习不同，如象棋游戏中，存在数万可以移动的玩法；但是在强化学习中，存在的是对个体的奖励反馈函数，而不是像监督学习直接告诉个体最终的答案。

• 无监督学习：不存在一个从输入到输出的映射过程。在强化学习中，有从输入到输出的映射过程，如强化学习通过用户的一些文章，并且获得用户的不断反馈，从而构建一个“知识图谱”，从而得知用户与文章之间的喜爱关系。
• 半监督学习：其本质是监督学习和无监督学习的组合。它不同于强化学习，半监督学习具有直接的参照答案，而强化学习不具有。

---

因此，强化学习的特点主要有以下两点：

• 强化学习是试错学习，由于没有直接的好或坏的明确反馈信息，智能体要以不断与环境进行交互，通过试错的方式来获得最佳策略。

• 延迟回报，强化学习的指导信息很少，而且往往是在事后（最后一个状态）才给出的，因此导致一个问题是获得正或者负回报以后，如何将回报分配给前面的状态。

4. 马尔科夫决策过程

4.1 概念

现在的问题是如何去形式化地描述一个强化学习问题，这样才可以进行推理？最常见的方法是将其表示为马尔可夫决策过程。

例如：一个之前不会象棋的小白和一个专业棋手对弈。刚开始小白对棋面并没有任何概念，只能随机乱下。
假设双方每一轮下完后都会得到立即回报，比如吃子回报为1，被吃回报为-1，其他回报为0。
可以想象一开始小白会输得很惨，但如果小白很聪明，随着不断地尝试小白不仅理解了下棋的规则，并且知道在什么棋面下做出什么动作可以吃更多的棋子。
在这里我们将小白作为我们的智能体 Agent，棋面就是状态State，下棋就是 Agent 根据当前 State 做出的行为action，每个动作执行完后都会引起状态改变。采取行动action 的原则Policy（比如高考数学中三角函数基础薄弱，采取的行动应该是偏重三角函数知识的学习）。

如果状态的改变只与前一个状态和当前的动作有关，而与之前其他的状态和动作无关（即满足马尔可夫性），那么整个过程可以用马尔可夫决策过程（Markov Decision Processes，MDP）来描述。

在书中将满足马尔可夫性的强化学习任务定义为马尔可夫决策过程，并将状态和动作都是有限空间的 MDP 定义为有限马尔可夫决策过程（finite MDP）。

4.2 理解 MDP 的动态过程

MDP 的动态过程如下：智能体在状态 s0s_0s0​ 选择某个动作 a0∈Aa_{0} \in Aa0​∈A，智能体根据概率 Ps0,a0P_{s_{0},a_{0}}Ps0​,a0​​ 转移到状态 s1s_1s1​，然后执行动作 a1a_1a1​，…如此下去我们可以得到这样的过程：
s0⟶a0s1(r1)⟶a1s2(r2)⟶a2s3(r3)⟶a3⋅⋅⋅s_{0} \stackrel{a_{0}}{\longrightarrow} s_{1} (r_1) \stackrel{a_{1}}{\longrightarrow} s_{2} (r_2)\stackrel{a_{2}}{\longrightarrow} s_{3} (r_3)\stackrel{a_{3}}{\longrightarrow} ···s0​⟶a0​​s1​(r1​)⟶a1​​s2​(r2​)⟶a2​​s3​(r3​)⟶a3​​⋅⋅⋅

4.3 给未来的奖励打折扣

给未来的奖励打折扣(Discounted Future Reward)。

要长期地表现良好，我们不仅要考虑当下的回报，还要考虑将来的回报，那么我们需要怎么做呢？
我们很容易计算一次马尔科夫决策在一个episode的总回报：
R=r1+r2+r3+...+rnR=r_1+r_2+r_3+...+r_nR=r1​+r2​+r3​+...+rn​
鉴于此，从时间t开始的总体的未来奖励可以表示为：
Rt=rt+rt+1+rt+2+...+rnR_t=r_t+r_{t+1}+r_{t+2}+...+r_nRt​=rt​+rt+1​+rt+2​+...+rn​
但由于环境是随机的，所以我们永远不能肯定，如果我们下一次执行相同的行动，我们会得到同样的回报，因为我们走向未来越多，分歧越多。所以，我们会给未来的奖励打个折扣。
因此，我们采用一个 $\gamma$ 超参数（0 和 1 之间的折扣因子），离当前时间点越远的奖励，我们就考虑得越少。很容易看出，我们在时间 $t$ 的对未来的回报折扣可以用时间 $t+1$ 时刻的回报来表示：
Rt=rt+γrt+1+γ2rt+2+...+γn−trn=rt+γ(rt+1+γ(rt+2+...))=rt+γRt+1R_t=r_t+\gamma r_{t+1}+\gamma ^2 r_{t+2}+...+\gamma^{n-t}r_n \\ =r_t+\gamma ( r_{t+1}+\gamma ( r_{t+2}+...))=r_t+\gamma R_{t+1}Rt​=rt​+γrt+1​+γ2rt+2​+...+γn−trn​=rt​+γ(rt+1​+γ(rt+2​+...))=rt​+γRt+1​
如果 $\gamma =0$，那么策略将会是短视的，将只重视即时的回报。如果想要平衡现在和将来的回报，应设置 $\gamma =0.9$。当然如果环境是确定的，则可以设置 $\gamma =1$。
对于 Agent 来说一个好的策略是能够使所选择的行动能够最大化（折扣后）未来的奖励。

5. Q-Learning

在这里我们定义一个函数 $Q(s,a)$ ：表示当在状态 $s$ 下执行 $a$ 行动后能获得的未来（折扣）奖励的最大值，并从该时间点继续优化。
Q(st,at)=max⁡Rt+1Q(s_t,a_t)=\max R_{t+1}Q(st​,at​)=maxRt+1​

$Q(s,a)$ 的另一种解释方式是：在状态 $s$ 执行动作 $a$ 能够在游戏结束时获得最好的评分，它被称为Q函数，因为它表示给定状态中某个动作的质量。

但如果我们仅仅知道现在的状态和行动，而不是之后的行动和奖励，我们不可能估计比赛结束时的状态。但作为理论构造，我们假设存在这么一个函数。

假设正处于某个状态，然后正在琢磨下一步到底是走 $a$ 还是 $b$ ，然后你想选一个能在游戏结束后获得最高分的那一步。一旦有了神奇的Q函数，思路就会变得很简单，就用最高的 Q 值来挑选动作。这里的 $\pi$ 代表一种策略，是我们在每一个状态选择动作的规则：
π(s)=argmaxa Q(s,a)\pi(s)=\underset{a}{\mathrm{ argmax} }\ Q(s,a) π(s)=aargmax​ Q(s,a)
那么我们如何来获得这个Q函数呢？（Q函数换种定义）贝尔曼公式：
Q(s,a)=r+γ max⁡a′Q(s′,a′)Q(s,a)=r+\gamma \ \max_{a'}Q(s',a')Q(s,a)=r+γ a′max​Q(s′,a′)

Q-Learning 的核心思想就是可以用贝尔曼方程迭代逼近Q函数。

算法中的 $\alpha$ 是学习率，它控制了以前的Q值和新提出的Q值的的差异有多少被考虑在内。特别的，当 $\alpha =1$ 时，则两个 $Q[s,a]$ 取消，得到的更新方法和贝尔曼方程完全相同。
用来更新 $Q[s,a]$ 的最大 $Q[s\prime ,a\prime ]$ 只是一个近似值，在学习的早期阶段可能是完全错误的，然而，随着每次迭代，近似值越来越准确，并且已经显示出如果这个值地到充分的更新，则Q函数将收敛并表示真实的Q值。

---

---

initialize Q[numstates,numactions]Q[\text{num}_{\text{states}},\text{num}_{\text{actions}}]Q[numstates​,numactions​] arbitrarily
observe initial state $s$
repeat
  select and carry out an action $a$
  observe reward $r$ and new state $s\prime$
  Q[s,a]=Q[s,a]+α(r+γ maxa′ Q[s′,a′]−Q[s,a])Q[s,a]=Q[s,a]+α(r+γ\ \underset{a′}{\mathrm{max} }\ Q[s′,a′]−Q[s,a])Q[s,a]=Q[s,a]+α(r+γ a′max​ Q[s′,a′]−Q[s,a])
  $s=s\prime$
until

---

---

参考文献

[1] http://blog.csdn.net/sinat_28751869/article/details/64442972

---

江湖问路不问心，问心问得几人行。