MATLAB数学实验——Jacobi迭代法&Gauss-Seidel迭代法

MATLAB数学实验——Jacobi迭代法&Gauss-Seidel迭代法

一、迭代算法的数学知识

线性方程组的数值求解方法，有经典的Jacobi和Gauss-Seidel迭代方法。
二者通过迭代，从而求解方程。
基本思路：
①将矩阵方程AX=b中的A分解为（U+L+D），即上三角矩阵、下三角矩阵和对角矩阵之和；
②将等式化为：X_k+1=BX_k+d的格式，从而求得X。

（1） Jacobi迭代法

A=U+L+D
AX=b
→(U+L+D)X=b
→DX=-(U+L)X+b
→DX=-(A-D)X+b
→X=(E+D^-1A)X+D^-1b=B_JX+d_J

X_k+1=B_JX_k+d_J
B_J=E+D^-1A;
d_J=D^-1b;

（2） Gauss-Seidel迭代法

A=U+L+D
AX=b
→(U+L+D)X=b
→(L+D)X=-UX+b
→X=-(L+D)^-1UX+(L+D)^-1b

X_k+1=B_GX_k+d_G
B_G=-(L+D)^-1U;
d_G=(L+D)^-1b;

二、Jacobi迭代法的MATLAB实现

调用格式：
X=Jacobi_2(A,b,X0,Norm,Error,Max,p)
Norm：范数的名称，Norm=1，2，inf；
error：近似解的误差；
Max：迭代的最大次数；
p：是否需要画图（不输入则不画），p=1，0，不输入

%用Jacobi迭代法解线性方程组Ax=b
%Norm：范数的名称，Norm=1，2，inf；
%error：近似解的误差；
%Max：迭代的最大次数；
function X=Jacobi_2(A,b,X0,Norm,Error,Max,p)
if nargin==6
    p=0;
end
a=[];
x=[];
[N N]=size(A);
X=X0;
[L,D,U]=LUD(A);
B=eye(N)-inv(D)*A;
d=inv(D)*b;
X1=A\b;
Result=lt_con(B);
if Result~=1
    error('迭代算法不收敛');
    return
end
disp '迭代算法收敛，继续计算...'
for i=1:Max
    X=B*X+d;
    errX=norm(X-X1,Norm);
    %X0=X;
    a(i)=errX;
    x=i;
    if errX=Error
    disp('请注意：Jacobi迭代次数已经超过最大迭代次数Max.')
end
if p==1
    plot(1:x,a);
end

end

三、Gauss迭代法的MATLAB实现

调用格式：
X=G_S(A,b,X0,Norm,Error,Max,p)
Norm：范数的名称，Norm=1，2，inf；
error：近似解的误差；
Max：迭代的最大次数；
p：是否需要画图（不输入则不画），p=1，0，不输入

%用Gauss-Seidel迭代法解线性方程组Ax=b
%Norm：范数的名称，Norm=1，2，inf；
%error：近似解的误差；
%Max：迭代的最大次数；
function X=G_S(A,b,X0,Norm,Error,Max,p)
if nargin==6
    p=0;
end
a=[];
x=[];
[N N]=size(A);
X=X0;
[L,D,U]=LUD(A);
B=-inv(D+L)*U;
d=inv(D+L)*b;
X1=A\b;
Result=lt_con(B);
if Result~=1
    error('迭代算法不收敛');
    return
end
disp '迭代算法收敛，继续计算...'
% disp '...'
% pause(0.1)
% disp '..'
% pause(0.1)
% disp '.'
% pause(1)
for i=1:Max
    X=B*X+d;
    errX=norm(X-X1,Norm);
    %X0=X;
    a(i)=errX;
    x=i;
    if errX=Error
    disp('请注意：Gauss-Seidel迭代次数已经超过最大迭代次数Max.')
end
if p==1
    plot(1:x,a);
end
end

四、例子

A=[2,-1,1; 3,6,2;3,3,7];
b=[15,5,8]';
X0=[0,0,0]';
Jacobi_2(A,b,X0,inf,1e-3,1000,1);
hold on
G_S(A,b,X0,inf,1e-3,1000,1);

例子结果：
（1）命令行窗口：

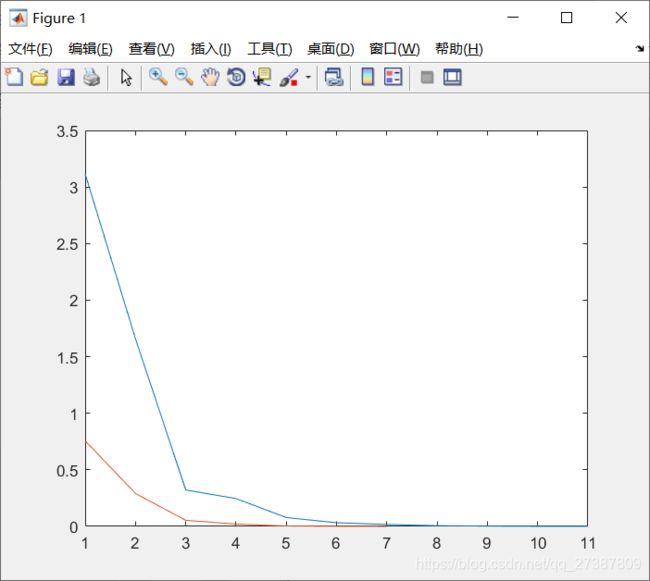
（2）绘图窗口（蓝色为Jacobi迭代误差，红色为Gauss-Seidel迭代误差，横轴为迭代次数）：

[20200212]更新：补充lt_con()子程序代码：

%计算迭代的收敛性，作为迭代的子程序
%
function Result=lt_con(B)
syms k;
l=length(B);
C=zeros(size(B));
for i=1:l
    C(i)=limit(B(i)^k,k,inf);
end
Crit=C;
%Crit=limit(B^k,k,inf);
if Crit==0
    Result=1;
else
    Result=0;
end
end

确保有这个子程序，迭代法才能顺利运行。

转载请注明出处