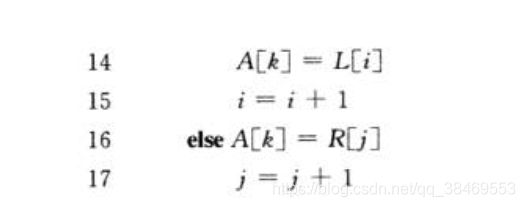堆排序,快速排序,归并排序,插入排序总结及C++实现
目录
1.堆排序
1.1堆
1.2维护堆的性质
1.3建堆
1.4堆排序算法
2.快速排序
3.归并排序
3.1原理
3.2代码实现
3.3时间复杂度
4.插入法排序
4.1原理
1.堆排序
1.1堆
堆是一个数组,可以看成一个近似的完全二叉树。除了最底层外树是完全充满的,并且从左到右填充。
表示堆的数组A有两个属性,一个是A.length,表示数组的大小;另一个是A.heapsize,表示数组中有多少个堆元素。
在堆中给定一个下标i,可以得到该节点的父节点和左右子节点的下标。
因为C++数组的习惯都是下标从0开始,而算法导论中的下标通用形式是从1开始,所以计算下标的公式略有不同:
PARENT(i) = (i-1)/2;
LEFT(i) = 2*i + 1;
RIGHT(i) = 2*i + 2;
最大堆:堆中所有子树的根节点的值都是该子树所有节点的最大值。
1.2维护堆的性质
void MaxHeapify(vector& arry,int i,int size)
{
//i为当前根节点下标,size为堆的大小,即size<=arry.size()
int l = 2*i+1;
int r = 2*i+2;
int largest = i;//注意此处需要将largest初始化为i,因为后续判断要用到
if(larry[i])
{
largest = l;
}
else
{
largest = i;
}
if(rarry[largest])
{
largest = r;
}
if(largest!=i)
{
int tmp = arry[i];
arry[i] = arry[largest];
arry[largest] = tmp;
MaxHeapify(arry,largest,size);
}
return ;
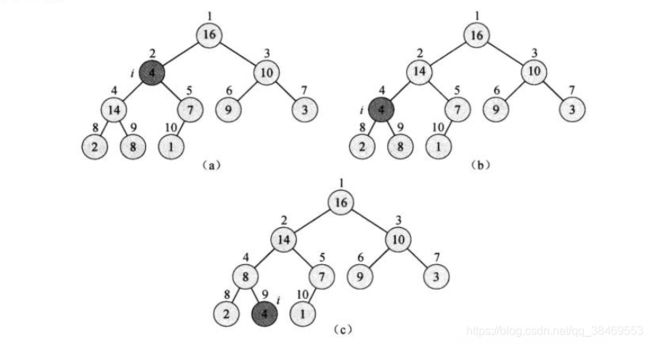
} 该函数是假定下标为i的节点的左子树和右子树都已经是最大堆,但是该节点为根节点的树不是最大堆。因此该函数将A[i]的值在最大堆中逐级下降,最终使得以下标i为根节点的子树成为最大堆。
主要思想就是每次对比A[i],A[l],A[r]三个节点值的大小,选出最大值后与根节点i交换。交换之后,节点i处的树满足了最大堆性质,但是节点largest处的树有可能就不满足了最大堆性质,因此递归地对以largest节点为根节点的子树调用该函数,最终使得以最初节点i为根的树满足最大堆性质。
时间复杂度:
1.3建堆
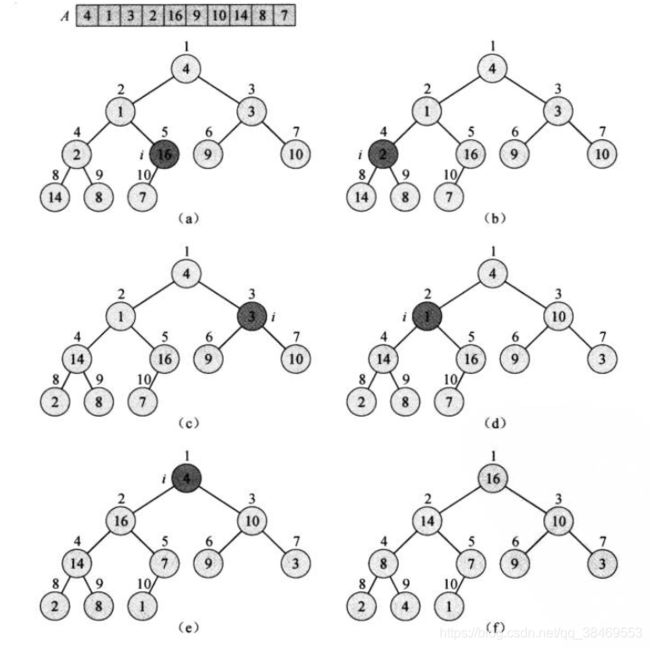
利用自底向上的方式建堆。
并且对于下标从0开始,大小为A.size()的堆,它的下标从A.size()/2到A.size()-1的节点都是叶子节点。
而叶子节点本身符合最大堆性质,因此从A.size()/2-1 downto 0来自底向上建立最大堆。
每次将堆中更下面的子树先构建好最大堆,然后往上去维护最大堆性质,直到下标为0的根节点。
void BuildMaxHeap(vector& arry)
{
for(int i=arry.size()/2-1;i>=0;--i)
{
MaxHeapify(arry,i,arry.size());
}
return ;
} 上述代码将整个arry构建为最大堆。
时间复杂度:
1.4堆排序算法
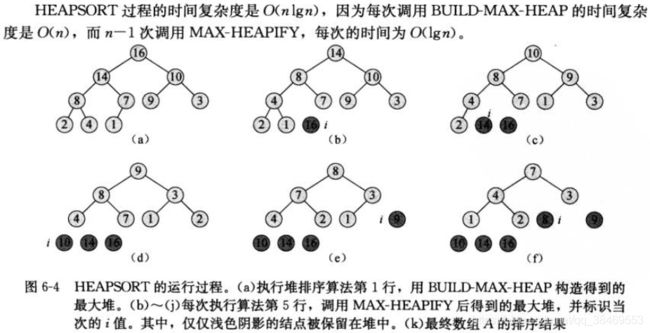
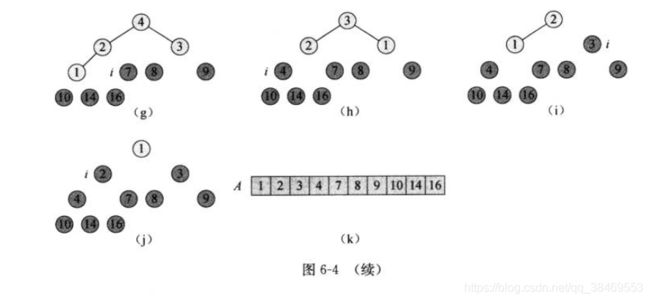
首先将待排序数组构建成为最大堆,令n=A.size(),此时数组中的最大值元素在A[0],将其与A[n-1]的元素互换,此时最大值元素在排序序列中的位置正确了,但是不满足最大堆性质了。因此将A[n-1]元素从堆中排除,令A.heapsize-=1,则新的堆中,除了刚才置换过的元素外,其他所有子树是满足最大堆性质的。
接下来则在新的堆中,用MaxHeapify维护最大堆性质,之后得到的最大堆中,A[0]为待排序数组中的次大值,再次将A[0]与A[n-2]互换。
重复该过程,直到堆大小为2.
void HeapSort(vector& arry)
{
BuildMaxHeap(arry);
for(int i=arry.size()-1;i>0;--i)
{
int tmp = arry[0];
arry[0] = arry[i];
arry[i] = tmp;
MaxHeapify(arry,0,i);
}
} 时间复杂度:最好情况,平均情况,最坏情况都是O(nlogn).
空间复杂度:原址排序,O(1).
稳定性:不稳定。
2.快速排序
原理:
快排是原址排序。对于一个待排序数列,选其最后一个数作为比较值(设其值为key),然后开始遍历该数列,将比key小的放在前面,比key大的放在后面。遍历结束后将这个key与分界线处的元素互换位置,并得到该index。
然后以这个index将数列分为前后两部分,对这两部分分别再进行排序,这是一个递归的过程。
代码:
int Part(vector& nums,int p,int r)
{
//初始化时,p从0开始,r从n-1开始
int key = nums[r];
int i = p - 1;//i保存的是小于key的序列的最后一个位置的index
for(int j = p;j < r;++j)
{
//当前元素>=key时不做操作
//当前元素<key时递增i值后,将小的元素换过来
if(nums[j] < key)
{
i += 1;
swap(nums[i],nums[j]);
}
}
i += 1;
swap(nums[i],nums[r]);
return i;
}
void QuickSort(vector& nums,int p,int r)
{
if(pr的时候会段错误
int mid = Part(nums,p,r);
QuickSort(nums,p,mid-1);
QuickSort(nums,mid+1,r);
}
return ;
} 时间复杂度:最好情况O(nlogn),平均情况O(nlogn),最坏情况O(N^2).
空间复杂度:原址排序O(1),但是算上递归调用的空间开销则平均情况是O(logn),最坏情况是O(n)。
稳定性:不稳定。
3.归并排序
3.1原理
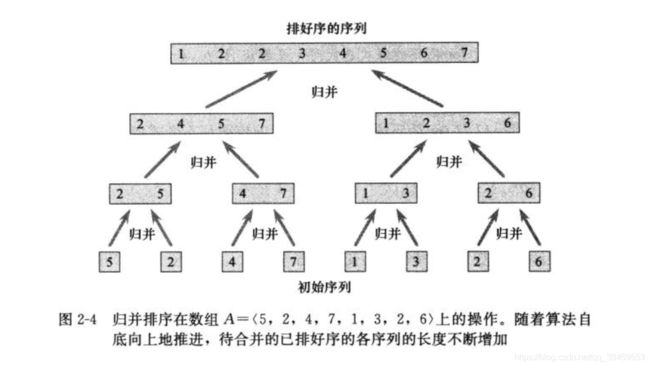
应用了分治法的思想,将待排序数组分解成子数组,将子数组排好序之后,对其进行排序则很简单,即相当于合并两个排好序的数组,并且可以在线性时间内完成该操作。示例图如下。
3.2代码实现
伪代码如下:
其中MERGE(A,p,q,r)函数用于将两个排好序的子数组合并。代码中先将待排序数组自上而下不断分割为子数组,直到子数组中元素个数为1,此时它就已经是排好序的数组了。然后再调用MERGE(A,p,q,r)函数自下而上将排好序的子数组合并,最终合并成原数组大小。分割之后的子数组的范围分别为A[p,q]和A[q+1,r],此处边界为左右都闭合的。
其中在L和R数组的末尾增加了一个哨兵牌,这样就免除了判断数组是否为空的麻烦。
C++代码如下:
void merge(vector& arry,int p,int q,int r)
{
int leftlen=q-p+1;int rightlen=r-q;
vectorLpart(arry.begin()+p,arry.begin()+q+1);
vectorRpart(arry.begin()+q+1,arry.begin()+r+1);
Lpart.push_back(INT_MAX);
Rpart.push_back(INT_MAX);
//int i=p;int j=q+1;
int i=0,j=0;
for(int k=p;k<=r;++k)
{
if(Lpart[i]<=Rpart[j])
{
arry[k]=Lpart[i];
++i;
}
else
{
arry[k]=Rpart[j];
++j;
}
}
return ;
}
void merge_sort(vector& arry,int p,int r)
{
if(p 代码中,p为数组的起始点的下标,r为数组的最后一个元素的下标,q为分割点,且有p≤q<r。
但是哨兵牌的方式中,若本身序列里就存在多个INT_MAX值,则这样的方法就不可行了。所以一般写法如下代码。此外归并排序还有一种非递归的写法,即循环的写法。代码如下。
#include
#include
#include
using namespace std;
void print(vector& nums)
{
for(auto c:nums)
cout<& nums,int left,int mid,int right)
{
//mid实际上为左边序列的最后一个元素
int size1 = mid - left + 1;
int size2 = right - mid;
vector Lpart(nums.begin()+left,nums.begin()+mid+1);
vector Rpart(nums.begin()+mid+1,nums.begin()+right+1);
//print(Lpart);print(Rpart);
int k = left;int i = 0;int j = 0;
while(k <= right&&i& nums,int left,int right)
{
//递归的写法
//index的区间都是左右闭合的
//注意需要判断left和right的大小
if(left& nums)
{
//非递归的方式归并排序
int len = nums.size();
for(int step = 1;step<=len;step*=2)
{
int left = 0;int right = 0;
for(left=0;left+step-1<=len-1;left+=step)
{
right = left + step - 1;
int mid = (left + right)/2;
Merge(nums,left,mid,right);
}
//当上一个循环退出时,left的值若不等于len,说明len不是2的幂次方,此时会有遗漏的元素没有排
//遗漏在末尾,因此需要将其再排一次,此时待排序的子序列中mid是前一个子序列的right值
//而此时的right值是nums.size()-1,此时的left需要-=step来退回到前一个子序列的左端点
if(left!=len)
{
left -= step;
int mid = right;
right = nums.size() - 1;
Merge(nums,left,mid,right);
}
print(nums);
}
}
int main()
{
vectornums={9,8,7,6,5,4,3,2,1};
//vectornums={7,6,5,4,3,2,1};
//MergeSort(nums,0,nums.size()-1);
MergeSort2(nums);
print(nums);
//输出排序过程:
//9 8 7 6 5 4 3 2 1
//8 9 6 7 4 5 1 2 3
//6 7 8 9 1 2 3 4 5
//1 2 3 4 5 6 7 8 9
return 0;
} 3.3时间复杂度
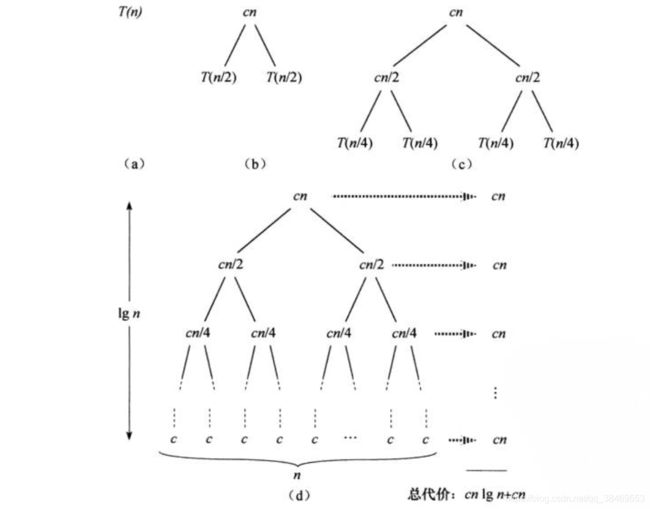
分治算法的时间复杂度一般式如下。
特别地对于归并排序来说,有:
该地归树每一层的时间为cn,一共有lgn+1层,因此最终忽略低阶项之后,时间复杂度为O(nlgn)。
并且由于每次合并两个排序数组需要额外的空间开销,归并排序的空间复杂度为O(n)。因为每次递归中辅助空间会被释放掉。递归写法的递归调用占用O(logn),循环写法则没有这额外的开销。
稳定性:稳定的
4.插入法排序
4.1原理
插入法排序是原址排序。对于一个序列来说,从第二个元素arry[i]开始,倒着将其与前面的每个元素比较,将大于它的元素往后挪一位,直到找到第一个小于等于它的元素,此时将这个arry[i]插入到这个位置即可。
代码如下:
#include
#include
#include
using namespace std;
void InsertSort(vector& nums)
{
int n = nums.size();
for(int i=1;i= 0 && nums[k] > key)
{
nums[k+1] = nums[k];
--k;
}
nums[k+1] = key;
}
return;
} 时间复杂度:平均情况和最坏情况是O(n^2);最好情况是O(n),此时数列已经排好序。
空间复杂度O(1),原址排序.
稳定性:稳定的。