Datawhale第7期-《李宏毅机器学习》作业(一)
任务:
1.了解什么是Machine learning
机器学习是什么
通过人为创造的程式让机器具备学习的能力,使之能解决特定的问题。更物质化一点讲,是从数据中寻找一个函数Function可以用来拟合数据。
2.学习中心极限定理,学习正态分布,学习最大似然估计
中心极限定理
中心极限定理证明了如下观点:一些现象受到许多相互独立的随机因素的影响,如果每个因素所产生的影响都很微小时,总的影响可以看作是服从正态分布的。
独立同分布的中心极限定理的数学表达:独立同分布的随机变量 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn且数学期望和方差存在, E x i = μ Ex_i=\mu Exi=μ, D x i = σ 2 Dx_i=\sigma ^2 Dxi=σ2,i=1,2,…,k。当n很大时,随机变量 Y n = ∑ i x i − n μ n σ Y_n= \dfrac{\sum_i{x_i-n\mu}}{\sqrt n \sigma} Yn=nσ∑ixi−nμ近似服从标准正态分布N(0,1),做个变形即 ∑ i x i \sum_i x_i ∑ixi近似服从均值为 n μ n\mu nμ,方差为 n σ 2 n\sigma ^2 nσ2的标准正态分布。
最大似然估计
最大似然估计是一种统计学习方法,用于求解样本集的相关概率密度函数的参数。给定概率分布D,通过抽取n个样本值 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn及利用概率密度函数 f D f_D fD得到参数空间的可能性表示: l i k e ( θ ) = f D ( x 1 , x 2 , . . . , x n ∣ θ ) like(\theta)=f_D(x_1,x_2,...,x_n|\theta) like(θ)=fD(x1,x2,...,xn∣θ),使like取最大的值即被称为参数 θ \theta θ的最大似然函数。
最大似然估计的性质:
1.泛函不变性
如果 θ h a t \theta_{hat} θhat是 θ \theta θ的一个最大似然估计,那么 α = g ( θ ) \alpha =g(\theta) α=g(θ)的最大似然估计是 α h a t = g ( θ h a t ) \alpha_{hat} =g(\theta_{hat}) αhat=g(θhat)。
2.渐近线行为
在采样样本总数趋于无穷的时候,最大似然估计函数达到最小方差。对于独立的观察来说,最大似然估计函数经常趋于正态分布。
最大似然估计的一般求解步骤:
(1)写出似然函数 L ( θ ) = ∏ i f ( x i ; θ ) L(\theta)=\prod_if(x_i;\theta) L(θ)=∏if(xi;θ)
(2)对似然函数两边取对数 l n L ( θ ) = ∑ i l n p ( x i ; θ ) lnL(\theta)=\sum_ilnp(x_i;\theta) lnL(θ)=∑ilnp(xi;θ)
(3)对 l n L ( θ ) lnL(\theta) lnL(θ)求导数并令之为0
学习损失函数与凸函数之间的关系
损失函数用于描述当前模型预估值有多差,其输入是一个函数( y = b + w ⋅ x y=b+w\cdot x y=b+w⋅x),在回归问题中,常见的损失函数有L1损失函数,L2损失函数;在分类问题中,常见的损失函数有交叉熵损失函数,指数损失函数等。
回归函数的损失函数
回归函数一般可以定义为 y = w T x + b y=w^Tx+b y=wTx+b,其损失函数为 L ( w , b ) = ∑ n ( y h a t n − ( w x n + b ) ) L(w,b)=\sum_n(y_{hat}^n-(wx^n+b)) L(w,b)=∑n(yhatn−(wxn+b)),其中上标n为第n个样本的特征值。
在梯度下降算法中,若损失函数非凸,则在选择不同的初始化点后,有可能出现局部最优解;而当损失函数为凸函数时,根据凸优化的相关定理,可以证明损失函数可以取到最小值。
了解全局最优和局部最优
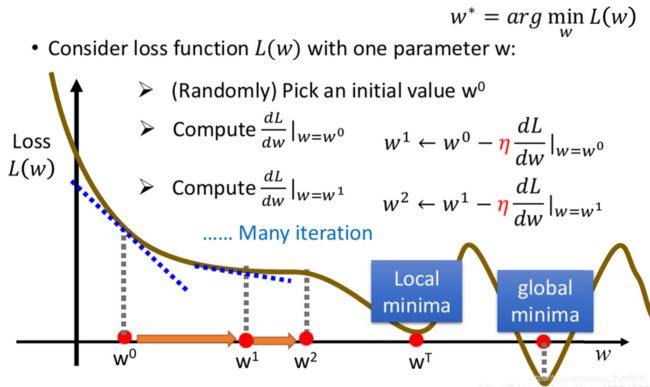
局部最优是指在当前点前后小范围内的损失函数达到最小,但从整体来看并不是最小值点,可能在其比较远的位置处还存在更小值。全局最优是指从整体来看损失函数达到最小的点。全局最优和局部最优的关系可以类比于最小值和极小值。
3.学习导数,泰勒展开
泰勒展开
函数f(x)在 x 0 x_0 x0处的泰勒展开式为: f ( x ) = f ( x 0 ) 0 ! + f ′ ( x 0 ) 1 ! ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + . . . f ( n ) ( x 0 ) n ! ( x − x 0 ) n + R n ( x ) f(x)=\dfrac{f(x_0)}{0!}+\dfrac{f'(x_0)}{1!} (x-x_0)+\dfrac{f''(x_0)}{2!}(x-x_0)^2+...\dfrac{f^{(n)}(x_0)}{n!} (x-x_0)^n+R_n(x) f(x)=0!f(x0)+1!f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+...n!f(n)(x0)(x−x0)n+Rn(x)
梯度下降基本方法
对损失函数求极小化,即 w ∗ , b ∗ = a r g min w L ( w ) w^*,b^*=arg\min_wL(w) w∗,b∗=argminwL(w),即可求解最优参数,其优化方法常采用梯度下降法,以下推导回归损失函数的优化方法:
- 随机选取 w 0 , b 0 w^0,b^0 w0,b0
- 计算 ∂ L ∂ w ∣ w = w 0 , b = b 0 \dfrac{\partial L}{\partial w}|_{w=w^0,b=b^0} ∂w∂L∣w=w0,b=b0, ∂ L ∂ b ∣ w = w 0 , b = b 0 \dfrac{\partial L}{\partial b}|_{w=w^0,b=b^0} ∂b∂L∣w=w0,b=b0
- 更新参数 w 1 = w 0 − α ∂ L ∂ w ∣ w = w 0 , b = b 0 w^1=w^0-\alpha\dfrac{\partial L}{\partial w}|_{w=w^0,b=b^0} w1=w0−α∂w∂L∣w=w0,b=b0
b 1 = b 0 − α ∂ L ∂ b ∣ w = w 0 , b = b 0 , b^1=b^0-\alpha\dfrac{\partial L}{\partial b}|_{w=w^0,b=b^0}, b1=b0−α∂b∂L∣w=w0,b=b0, - 重复以上流程
注:在更新参数一步中,用到的参数 α \alpha α称为学习率,表示每次参数更新的步长。
回归模型的损失函数为 L ( w , b ) = ∑ n ( y h a t n − ( w x n + b ) ) L(w,b)=\sum_n(y_{hat}^n-(wx^n+b)) L(w,b)=∑n(yhatn−(wxn+b)),
则 ∂ L ∂ w = ∑ n 2 ( y h a t n − ( w x n + b ) ) ( − x n ) \dfrac{\partial L}{\partial w}=\sum_n2(y_{hat}^n-(wx^n+b))(-x^n) ∂w∂L=∑n2(yhatn−(wxn+b))(−xn), ∂ L ∂ b = ∑ n 2 ( y h a t n − ( w x n + b ) ) ( − 1 ) \dfrac{\partial L}{\partial b}=\sum_n2(y_{hat}^n-(wx^n+b))(-1) ∂b∂L=∑n2(yhatn−(wxn+b))(−1)
梯度下降原理
依据泰勒公式对函数f(x)做一阶展开和二阶展开: f ( x ) ≈ f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) f(x)\approx f(x_0)+f'(x0)(x-x_0) f(x)≈f(x0)+f′(x0)(x−x0)以及 f ( x ) ≈ f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + f ′ ′ ( x 0 ) ( x − x 0 ) 2 / 2 f(x)\approx f(x_0)+f'(x_0)(x-x_0)+f''(x_0)(x-x_0)^2/2 f(x)≈f(x0)+f′(x0)(x−x0)+f′′(x0)(x−x0)2/2
假设: x t = x t − 1 + δ x x^t=x^{t-1}+\delta x xt=xt−1+δx,
则根据泰勒公式的二阶展开, f ( x t ) ≈ f ( x t − 1 + δ x ) f ( x t − 1 ) + f ′ ( x t − 1 ) δ x + f ′ ′ ( x t − 1 ) δ x 2 / 2 f(x^t)\approx f(x^{t-1}+\delta x)f(x^{t-1})+f'(x^{t-1})\delta x +f''(x^{t-1})\delta x^2/2 f(xt)≈f(xt−1+δx)f(xt−1)+f′(xt−1)δx+f′′(xt−1)δx2/2,根据参数更新的方式令 θ t = θ t − 1 + δ θ \theta^t=\theta^{t-1}+\delta \theta θt=θt−1+δθ,则损失函数(损失函数可以认为是参数的函数)为 L ( θ t ) = L ( θ t − 1 + δ θ ) ≈ L ( θ t − 1 ) + L ′ ( θ t − 1 ) δ θ L(\theta ^t)=L(\theta^{t-1}+\delta \theta)\approx L(\theta^{t-1})+L'(\theta^{t-1})\delta\theta L(θt)=L(θt−1+δθ)≈L(θt−1)+L′(θt−1)δθ。参数更新的目标是使损失函数不断减少,即使得 L ( θ t ) < L ( θ t − 1 ) L(\theta^t)<L(\theta^{t-1}) L(θt)<L(θt−1),那么 L ′ ( θ t − 1 ) δ θ < 0 L'(\theta^{t-1})\delta\theta<0 L′(θt−1)δθ<0,其中 θ t − 1 \theta^{t-1} θt−1及 δ θ \delta\theta δθ均为向量,为保证其乘积小于0,可取 δ θ = − α L ′ ( θ t − 1 ) \delta\theta=-\alpha L'(\theta^{t-1}) δθ=−αL′(θt−1)
写出梯度下降的代码
# 基于回归函数编写梯度下降算法
import numpy as np
np.random.seed(2019)
# 定义输入
x = np.linspace(0,10,100)
y = 1+2*x
# 初始化参数
w = np.random.randn(1,1)
b = np.zeros((1,1))
epochs=100
lr = 0.0001
def fx(x,w,b):
return w*x+b
def gd(x,y,w,b):
epoch=0
f = fx(x,w,b)
loss = np.sum((y-fx(x,w,b)**2))
while loss>1 or epoch4.学习L2-Norm,L1-Norm,L0-Norm
当模型在训练集上的正确率高但在验证集上正确率低时即发生过拟合,在发生过拟合后可以通过在原损失函数基础上添加正则项,从而约束某些参数权值过高。
具体来说,在损失函数中添加正则项 L = ∑ n ( y h a t n − ( b + ∑ w i x i ) ) 2 + λ ∑ ( w i ) 2 L=\sum_n(y_{hat}^n-(b+\sum w_ix_i))^2+\lambda \sum(w_i)^2 L=∑n(yhatn−(b+∑wixi))2+λ∑(wi)2,则在不断减小损失函数的过程中,模型参数是受到约束从而不会很大,在李老师的课程中提到,参数 w i w_i wi越小,output对输入的变化是不敏感的(例如输入值受到噪声影响,波动为 δ x i \delta x_i δxi,那么输出的变化为 ∑ w i δ x i \sum w_i \delta x_i ∑wiδxi,如果此处的 w i w_i wi比较小,那么该噪声对输出的影响也会相应变小),也就是输出越平滑且模型效果越好。

对 λ \lambda λ取不同值会影响模型的最终效果,当 λ \lambda λ越大,表示考虑约束项越多,会使输出fx越平滑,那么在test data中的误差会越来越小,但是由于 λ \lambda λ越大会倾向于考虑参数原本的值而不是训练过程中的误差,所以在训练集中的error反而会随着 λ \lambda λ变大,在testing数据中,当 λ \lambda λ很大时误差反而会变小,所以需要选择合适的 λ \lambda λ。
L2-Norm,L1-Norm,L0-Norm
L1,L2和L0正则均是在原损失函数的基础上增加一个约束项,并用 λ \lambda λ去调节。
| 正则化方式 | 数学表达 |
|---|---|
| L0-Norm | ∑ j = 1 , θ j ≠ 0 m θ j 0 \sum_{j=1,\theta_j \neq 0}^{m}{\theta _j^0} ∑j=1,θj̸=0mθj0 |
| L1-Norm | ∑ j = 1 m a b s ( θ j ) \sum_{j=1}^{m}{abs(\theta _j)} ∑j=1mabs(θj) |
| L2-Norm | ∑ j = 1 m θ j 2 \sum_{j=1}^{m}{\theta _j}^2 ∑j=1mθj2 |
其中L0范数指向量中非0的元素个数,
- L1正则与L2正则使用场景
使用L1正则化时,倾向于得到稀疏向量,其主要是将较小的权重归为0,这种正则化会用于高维数据,用于帮忙选择数据;L2正则保证所有权重一致较小,可以训练一般的模型,得到好的结果。
为什么用L1-Norm代替L0-Norm
学术界普遍用L1代替L0做稀疏约束,一是因为L0难以优化求解,二是在一定条件下L1与L0求解目标等价且L1是L0的最优凸近似。
为什么只对w/Θ做限制,不对b做限制
因为w通常是一个高维参数矢量,w几乎涵盖了所有参数,b只是众多参数的中的一个,这样加上b来做regularization的作用不大,也可以加,只是作用不大
参考资料
1.https://baike.baidu.com/item/中心极限定理/829451?fr=aladdin
2.https://baike.baidu.com/item/最大似然估计/4967925?fr=aladdin
3. https://blog.csdn.net/zouxy09/article/details/24971995/
4.https://github.com/datawhalechina/Leeml-Book/blob/master/docs/chapter2/chapter2.md
5.https://blog.csdn.net/qq_40981899/article/details/90166398