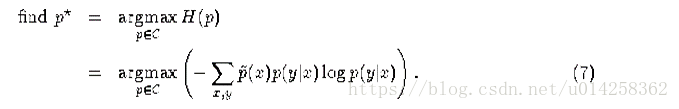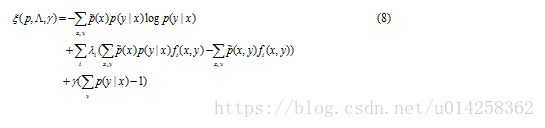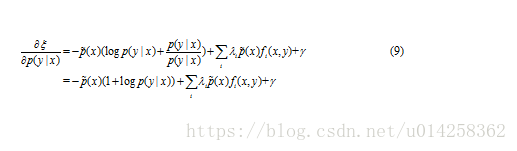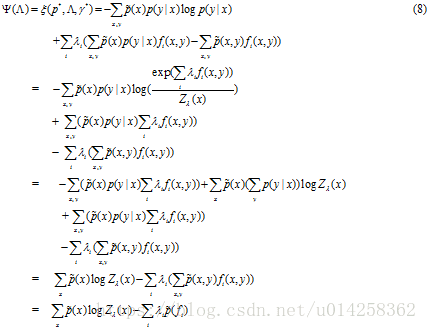NLP学习记录（六）最大熵模型MaxEnt

原理

在叧掌握关于未知分布的部分信息的情况下，符合已知知识的概率分布可能有夗个，但使熵值最大的概率分布最真实地反映了事件的的分布情况，因为熵定义了随机变量的不确定性，弼熵值最大时，随机变量最不确定，最难预测其行为。

---

最大熵模型介绍

我们通过一个简单的例子来介绍最大熵概念。假设我们模拟一个翻译专家的决策过程，关于英文单词in到法语单词的翻译。我们的翻译决策模型p给每一个单词或短语分配一个估计值p(f),即专家选择f作为翻译的概率。为了帮助我们开发模型p，我们收集大量的专家翻译的样本。我们的目标有两个，一是从样本中抽取一组决策过程的事实（规则），二是基于这些事实构建这一翻译过程的模型。

我们能从样本中得到的一个明显的线索是允许的翻译候选列表。例如，我们可能发现翻译专家总是选择下面这5个法语词汇：{dans, en, à, au cours de, pendant}。一旦有了这些信息，我们可以给模型p施加第一个约束条件：

p(dans)+p(en)+ p(à)+p(au cours de)+p(pendant) = 1

这个等式代表了这一翻译过程的第一个统计信息，我们现在可以进行寻找满足这一条件的模型了。显然，有无数满足这个条件的模型可供选择。其中一个模型是p(dans)=1，换句话说这个模型总是预测dans。另外一个满足这一约束的模型是p(pendant)=1/2 and p(à)=1/2。 这两个模型都有违常理：只知道翻译专家总是选择这5个法语词汇，我们哪知道哪个概率分布是对的。两个模型每个都在没有经验支持的情况下，做了大胆的假设。最符合直觉的模型是：

p(dans) = 1/5

p(en) = 1/5

p(à) = 1/5

p(au cours de) = 1/5

p(pendant) = 1/5

这个模型将概率均匀分配给5个可能的词汇，是与我们已有知识最一致的模型。我们可能希望从样本中收集更多的关于翻译决策的线索。假设我们发现到有30％时间in被翻译成dans 或者en. 我们可以运用这些知识更新我们的模型，让其满足两个约束条件：

p(dans) + p(en) = 3/10

p(dans)+p(en)+ p(à)+p(au cours de)+p(pendant) = 1

同样，还是有很多概率分布满足这两个约束。在没有其他知识的情况下，最合理的模型p是最均匀的模型，也就是在满足约束的条件下，将概率尽可能均匀的分配。

p(dans) = 3/20

p(en) = 3/20

p(à) = 7/30

p(au cours de) = 7/30

p(pendant) = 7/30

假设我们又一次检查数据，这次发现了另外一个有趣的事实：有一般的情况，专家会选择翻译成dans 或 à.我们可以将这一信息列为第三个约束：

p(dans) + p(en) = 3/10

p(dans)+p(en)+ p(à)+p(au cours de)+p(pendant) = 1

p(dans)+ p(à)=1/2

我们可以再一次寻找满足这些约束的最均匀分配的模型p,但这一次的结果没有那么明显。由于我们增加了问题的复杂度，我们碰到了两个问题：首先，”uniform（均匀）”究竟是什么意思？我们如何度量一个模型的均匀度（uniformity）？第二，有了这些问题答案之后，我们如何找到满足一组约束且最均匀的模型？就像前面我们看到的模型。

最大熵的方法回答了这两个问题。直观上讲，很简单，即：对已知的知识建模，对未知的不过任何假设（model all that is known and assume nothing about that which is unknown）。换句话说，在给定一组事实（features+output）的条件下，选择符合所有事实，且在其他方面近可能均匀的模型，这恰恰是我们在上面例子每一步选择模型p所采取的方法。

• Maxent Modeling

我们考虑一个随机过程，它产生一个输出y，y属于一个有穷集合。对于刚才讨论的翻译的例子，该过程输出单词in的翻译，输出值y可以是集合｛dans, en, à, au cours de, pendant｝中任何一个单词。在输出y时，该过程可能会被上下文信息x影响，x属于有穷的集合X。在目前的例子中，这信息可能包括英文句子中in周围的单词。

我们的任务是构造一个统计模型，该模型能够准确表示随机过程的行为。该模型任务是预测在给定上下文x的情况下，输出y的概率：p(y|x).
Training Data

为了研究这一过程，我们观察一段时间随机过程的行为，收集大量的样本：。在我们讨论的例子中，每一个样本由包含in周围单词的词汇x，和in的翻译y组成。现在，我们可以假设这些训练样本已经由一个专家搞定了，我们提供大量包含in的随机的短语要求她选择一个合适的翻译。

我们可以通过它的经验分布来总结训练样本的特性：

 

 

通常，对于一个特定的pair （x, y），它要么不出现在样本中，要么最多出现几次。

• Features and constraints

我们的目标是构造一个产生训练样本这一随机过程的统计模型。组成这个模型的模块将是一组训练样本的统计值。在目前的例子中，我们已经采用了几个统计数据：（1）in被翻译成dans 或者en的频率是3/10;(2) in被翻译成dans 或 à的概率是1/2 ；…等。这些统计数据是上下文独立的，但我们也可以考虑依赖上下文信息x的统计数据。例如，我们可能注意到，在训练样本中，如果 April 是一个出现在in之后，那么in翻译成en的频率有9/10.

为了表示这个事件(event)，即当Aprial出现在in之后，in被翻译成en，我们引入了指示函数：

特征f 关于经验分布的期望值，正是我们感兴趣的统计数据。我们将这个期望值表示为：

(1)

我们可以将任何样本的统计表示成一个适当的二值指示函数的期望值，我们把这个函数叫做特征函数（feature function）或简称特征（feature）。

当我们发现一个统计量，我们觉得有用时，我们让模型去符合它（拟合），来利用这一重要性。拟合过程通过约束模型p分配给相应特征函数的期望值来实现。特征f关于模型p(y|x)的期望值是：

(2)

这里，是x在训练样本中的经验分布。我们约束这一期望值和训练样本中f的期望值相同。那就要求：

(3)

组合(1),(2) 和(3)，我们得到等式：

我们称（3）为约束等式（constraint equation）或者简称约束（constraint）。我们只关注那么满足（3）的模型，不再考虑那些和训练样本中特征f频率不一致的模型。

目前总结来看，我们现在有办法表示样本数据中内在的统计现象（叫做），也有办法使我们的模型继承这一现象（叫做）。

最后，仍我关于特征和约束再罗嗦两句：单词 feature'' andconstraint”在讨论最大熵时经常被混用，我们希望读者注意区分这两者的概念：特征（feature）是（x,y）的二值函数；约束是一个等式：即模型的特征函数期望值等于训练样本中特征函数的期望值。

• The maxent prinple

假设给我们n个特征函数fi，它们的期望值决定了在建模过程中重要的统计数据。我们想要我们的模型符合这些统计，就是说，我们想要模型p属于的子集C。

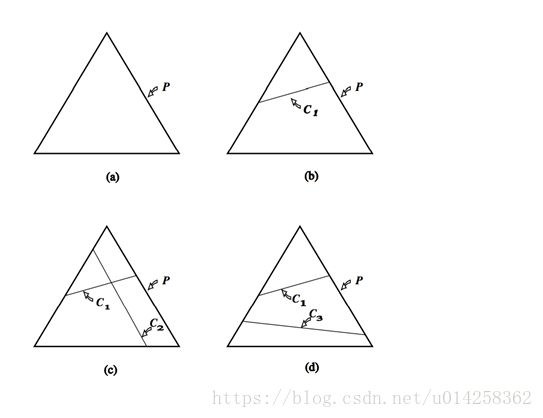
图1是这一限制的几何解释。这里，P是三点上所有可能的概率分布空间。如果我们不施加任何约束（图a），所有概率模型都是允许的。施加一个线性约束C1后，模型被限制在C1定义的区域，如图b示。如果两个约束是可满足的, 施加第二个线性约束后可以准确确定p，如图c所示。另一种情形是，第二个线性约束与第一个不一致，例如，第一个约束可能需要第一个点的概率是1/3，第二个约束需要第三个点的概率是3/4，图d所示。在目前的设置中，线性约束是从训练数据集中抽取的，不可能手工构造，因此不可能不一致。进一步来说，在我们应用中的线性约束甚至不会接近唯一确定的p,就象图c那样。相反，集合C=C1∩C2∩C3∩…∩Cｎ中的模型是无穷的。

属于集合C的所有模型p中，最大熵的理念决定我们选择最均匀的分布。但现在，我们面临一个前面遗留的问题：什么是”uniform(均匀)”？

数学上，条件分布p(y|x)的均匀度就是条件熵定义：

熵的下界是0, 这时模型没有任何不确定性；熵的上界是log|Y|,即在所有可能(|Y|个)的y上均匀分布。有了这个定义，我们准备提出最大熵原则。

当从允许的概率分布集合C中选择一个模型时，选择模型，使得熵H(p)最大。

可以证明是well-defined的，就是说，在任何的约束集合C中，总是存在唯一的模型取得最大熵。

• Exponential form

最大熵原理呈现给我们的是一个约束优化问题：find the which maximizes H(p)。简单的情况，我们可以分析求出问题的解。如翻译模型中我们施加前两个约束时，容易求得p的分布。不幸的是，通常最大熵模型的解无法明显得出，我们需要一个相对间接的方法。

为了解决这个问题，我们采用约束优化理论中Lagrange multipliers的方法。这里仅概述相关步骤，请参考进一步阅读以更深入了解约束优化理论如何应用到最大熵模型中的。

我们的约束优化问题是：

我们将这个称为原始问题（primal）。简单的讲，我们目标是在满足以下约束的情况下，最大化H(p)。

为了解决这个优化问题，引入Lagrangian 乘子。

实值参数和对应施加在解上的n+1个约束。

下面的策略可以求出p的最优解（），但我们不打算证明它。

首先，将和看成常量，寻找p最大化公式（8）。这会产生以和为参数的表示式p，（参数没有解决）。接着，将该表达式代回（8）中，这次求和的最优解（ and ,respectively）。

按照这一方式，我们保证和不变，计算在所有空间下，计算的无约束的最大值。

令该式等于0, 求解 p(y|x):

可以看出公式（10）的第二个因子对应第二个约束：

将上式带入公式（10）得到：

将公式（11）带入（10），我们得到：

因此，

Z(x)是正则化因子。

现在我们要求解最优值, 。显然，我们已经知道了 ，还不知道。

为此，我们介绍新的符号，定义对偶函数：

对偶优化问题是：

因为p*和是固定的，公式（15）的右边只有自由变量。

参数值等于的p*就是一开始约束优化问题的最优解。这办法不明显看出为什么，但这的确是Lagrange multipliers理论的基本原理，通常叫做Kuhn-Tucker theorem(KTT)。详细的解释已经超出本文讨论的范围。我们简单地陈述最后结论：

满足约束C最大熵模型具有（13）参数化形式，最优参数可以通过最小化对偶函数求得。

补充说明：

究竟是什么样呢？ (记住我们要求的最小值， 这是Lagrange multipliers理论的基本原理)

• Maximum likelihood

最大似然率：找出与样本的分布最接近的概率分布模型。

比如：10次抛硬币的结果是：

画画字画画画字字画画

假设p是每次抛硬币结果为”画”的概率。

得到这样试验结果的概率是：

P = pp(1-p)ppp(1-p)(1-p)pp=p7(1-p)3

最大化似然率的方法就是：

最优解是：p=0.7

似然率的一般定义为：

p(x)是模型估计的概率分布，是结果样本的概率分布。

在我们的问题里，要估计的是p(y|x)，最大似然率为：

因此，有：

这里的p具有公式（13）的形式，我们的结果进一步可以表述为：

最大熵模型是具有公式（13）形式，且最大化样本似然率的模型。最大熵模型与最大似然率模型一致。

• Computing the Parameters

要算λ，解析解肯定是行不通的。对于最大熵模型对应的最优化问题，GIS，lbfgs，sgd等等最优化算法都能解。相比之下，GIS大概是最好实现的。这里只介绍GIS算法。

具体步骤如下：

（1）set 等于任意值, 比如等于0.

(2) 重复直到收敛：

这里，(t)是迭代下标，常数C定义为：
, 实践中C是训练样本里最大的特征个数。尽管C再大些也没关系，但是它决定了收敛速度，还是取最小的好。

实际上，GIS算法用第N次迭代的模型来估算每个特征在训练数据中的分布。如果超过了实际的，就把相应参数变小。否则，将它们变大。当训练样本的特征分布和模型的特征分布相同时，就求得了最优参数。

• 最大熵实现

下面是GIS训练算法的python实现，代码不到100行。

from collections import defaultdict

import math


class MaxEnt(object):

    def __init__(self):

        self.feats = defaultdict(int)

        self.trainset = []

        self.labels = set()  



    def load_data(self,file):

        for line in open(file):

            fields = line.strip().split()

            # at least two columns

            if len(fields) < 2: continue

            # the first column is label

            label = fields[0]

            self.labels.add(label)

            for f in set(fields[1:]):

                # (label,f) tuple is feature 

                self.feats[(label,f)] += 1

            self.trainset.append(fields)



    def _initparams(self):

        self.size = len(self.trainset)

        # M param for GIS training algorithm

        self.M = max([len(record)-1 for record in self.trainset])

        self.ep_ = [0.0]*len(self.feats)

        for i,f in enumerate(self.feats):

            # calculate feature expectation on empirical distribution

            self.ep_[i] = float(self.feats[f])/float(self.size)

            # each feature function correspond to id

            self.feats[f] = i

        # init weight for each feature

        self.w = [0.0]*len(self.feats)

        self.lastw = self.w



    def probwgt(self,features,label):

        wgt = 0.0

        for f in features:

            if (label,f) in self.feats:

                wgt += self.w[self.feats[(label,f)]]

        return math.exp(wgt)



    """

    calculate feature expectation on model distribution

    """        

    def Ep(self):

        ep = [0.0]*len(self.feats)

        for record in self.trainset:

            features = record[1:]

            # calculate p(y|x)

            prob = self.calprob(features)

            for f in features:

                for w,l in prob:

                    # only focus on features from training data.

                    if (l,f) in self.feats:

                        # get feature id

                        idx = self.feats[(l,f)]

                        # sum(1/N * f(y,x)*p(y|x)), p(x) = 1/N

                        ep[idx] += w * (1.0/self.size)

        return ep



    def _convergence(self,lastw,w):

        for w1,w2 in zip(lastw,w):

            if abs(w1-w2) >= 0.01:

                return False

        return True



    def train(self, max_iter =1000):

        self._initparams()

        for i in range(max_iter):

            print 'iter %d ...'%(i+1)

            # calculate feature expectation on model distribution

            self.ep = self.Ep()           

            self.lastw = self.w[:]  

            for i,win enumerate(self.w):

                delta = 1.0/self.M * math.log(self.ep_[i]/self.ep[i])

                # update w

                self.w[i] += delta

            print self.w

            # test if the algorithm is convergence

            if self._convergence(self.lastw,self.w):

                break



    def calprob(self,features):

        wgts = [(self.probwgt(features, l),l) for l in self.labels]

        Z = sum([ w for w,l in wgts])

        prob = [ (w/Z,l) for w,l in wgts]

        return prob 



    def predict(self,input):

        features = input.strip().split()

        prob = self.calprob(features)

        prob.sort(reverse=True)

        return prob   

原文参考
https://blog.csdn.net/erli11/article/details/24718655