06_LR和最大熵模型_统计学习方法
文章目录
- 一、理解LR模型
- 1、 对数几率
- 2、函数映射
- 3、概率解释
- 二、LR模型参数估计
- 梯度下降求解最优参数
- 多项逻辑斯谛回归(multi-nominal logistic regression model)
- softmax
- 三、最大熵模型
- 1、最大熵原理
- 2、最大熵模型的定义
- 3、最大熵模型的学习
- 4、LR、softmax和最大熵模型之间的关系
- 5、最大熵模型和决策树模型的比对分析
- 四、模型学习的最优化方法
- 1、改进的迭代尺度法(IIS)
- 2、拟牛顿法
回归模型重要的基础或者方法就是回归分析,回归分析是研究一个变量(被解释变量)关于另一个(些)变量(解释变量)的具体依赖关系的计算方法和理论,是建模和分析数据的重要工具。—这段来自百度百科。
回归分为线性回归和非线性回归。
-
线性回归,因变量和自变量满足关系: y = w ⋅ x + b y = w\cdot x + b y=w⋅x+b
-
非线性回归,因变量和自变量不满足上面的关系,但是又有某种稳定的关系,统称为非线性回归。
线性回归比较直观,研究起来也简单。对于一些特别的非线性回归,可以转化成线性回归来研究。例如前面的感知机模型 y = s i g n ( w ⋅ x + b ) y = sign(w\cdot x+ b) y=sign(w⋅x+b)就可以分两步研究,可以有:
z = w ⋅ x + b (1) z = w\cdot x + b \tag 1 z=w⋅x+b(1)
y = s i g n ( z ) (2) y = sign(z) \tag 2 y=sign(z)(2)
对于式(1),就是熟悉和简单的线性回归问题。对于式(2)很简单, z ≥ 0 z\geq 0 z≥0为1, z < 0 z<0 z<0为-1。
而今天要学习的LR模型,与感知机模型类似,只是外面套的那层马甲不一样。LR模型 y = h θ ( x ) = s i g m o i d ( w ⋅ x + b ) y = h_{\theta}(x) = sigmoid(w\cdot x + b) y=hθ(x)=sigmoid(w⋅x+b), h θ ( x ) h_{\theta}(x) hθ(x)是模型的抽象函数, θ \theta θ是模型参数,sigmoid是LR模型具体使用的函数,w,b为模型具体参数。LR为什么要使用sigmoid函数?对为什么使用sigmoid函数做了一定解释。LR也可以成两步来研究,即:
z = w ⋅ x + b z = w\cdot x + b z=w⋅x+b
y = s i g m o i d ( z ) y = sigmoid(z) y=sigmoid(z)
在机器学习中,难点不在模型,而在根据问题来选择模型,这个需要对问题有足够的了解,要根据数据特征进行分析,再来选定合适的模型。当然按Andrew Ng说的做项目就要快速搭建框架,可以先选择一个模型完成一个整体框架,这个思路也非常好。对于模型的选择,后续再仔细研究研究,这是机器学习非常关键的一点。要选择模型,那么首先要了解被选择的模型。
一、理解LR模型
z = w ⋅ x + b z = w\cdot x + b z=w⋅x+b
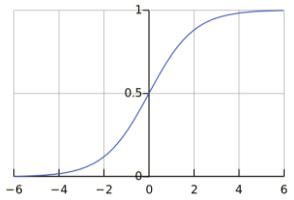
y = h θ ( x ) = s i g m o i d ( z ) = 1 1 + e − z y = h_{\theta}(x) = sigmoid(z) = \dfrac{1}{1+ e^{-z}} y=hθ(x)=sigmoid(z)=1+e−z1
1、 对数几率
一个事件的几率(odds)是指该事件发生的概率与该事件不发生的概率的比值。若事件发生概率为p,则该事件的几率是 p 1 − p \dfrac{p}{1−p} 1−pp,对数几率是 l o g p 1 − p log\dfrac{p}{1−p} log1−pp,对logistic回归而言:
l o g y 1 − y = l o g 1 1 + e − z e − z 1 + e − z = l o g e z = z = w ⋅ x + b log\dfrac{y}{1−y} = log\dfrac{\dfrac{1}{1+ e^{-z}}}{\dfrac{e^{-z}}{1+ e^{-z}}} = log\space e^z = z = w\cdot x + b log1−yy=log1+e−ze−z1+e−z1=log ez=z=w⋅x+b
输出y的对数几率是由输入x的线性函数表示的模型即为LR模型。
2、函数映射
考虑对输入实例x进行分类的线性表达式 w ⋅ x + b w\cdot x+b w⋅x+b,其值域为实数域,通过LR模型的表达式可以将线性函数 w ⋅ x + b w\cdot x+b w⋅x+b的结果映射到(0,1)区间,取值表示结果为1的概率(在二分类场景中)。线性函数的值越接近于正无穷大,概率值就越近1;反之,其值越接近于负无穷,概率值就越接近于0,这样的模型就是LR模型。LR本质上还是线性回归,只是特征到结果的映射过程中加了一层函数映射,即sigmoid函数,即先把特征线性求和,然后使用sigmoid函数将线性和约束至(0,1)之间,结果值用于二分或回归预测。
3、概率解释
LR模型多用于解决二分类问题,如广告是否被点击(是/否),商品是否被购买(是/否)等互联网领域中常见的应用场景。但在实际场景中,我们又不把它处理成绝对的分类,而是用其预测值作为事件发生的概率。这里从事件,变量以及结果的角度给予解释。
我们所能拿到的训练数据统称为观测样本。样本是如何生成的?一个样本可以理解为发生的一次事件,样本生成的过程即事件发生的过程,对于0/1分类问题来讲,产生的结果有两种可能,符合伯努利试验的概率假设。因此,我们可以说样本的生成过程即为伯努利试验过程,产生的结果(0/1)服从伯努利分布,那么对于第i个样本,概率公式表示如下:
P ( y ( i ) = 1 ∣ x ( i ) ; θ ) = h θ ( x ( i ) ) P(y^{(i)} = 1|x^{(i)};\space \theta) = h_{\theta}(x^{(i)}) P(y(i)=1∣x(i); θ)=hθ(x(i))
P ( y ( i ) = 0 ∣ x ( i ) ; θ ) = 1 − h θ ( x ( i ) ) P(y^{(i)} = 0|x^{(i)};\space \theta) = 1 - h_{\theta}(x^{(i)}) P(y(i)=0∣x(i); θ)=1−hθ(x(i))
将上面两个公式合并在一起,可以得到第i个样本正确预测的概率:
P ( y ( i ) ∣ x ( i ) ; θ ) = [ h θ ( x ( i ) ) ] y ( i ) [ 1 − h θ ( x ( i ) ) ] ( 1 − y ( i ) ) P(y^{(i)}|x^{(i)};\space \theta) = [h_{\theta}(x^{(i)})]^{y^{(i)}}\space[1 - h_{\theta}(x^{(i)})]^{(1- y^{(i)}\space )} P(y(i)∣x(i); θ)=[hθ(x(i))]y(i) [1−hθ(x(i))](1−y(i) )
上式是对一个样本进行建模的数据表达。那么对于所有的样本,假设每条样本生成过程独立,在整个样本空间中(N个样本)的概率分布(即似然函数)为:
P ( Y ∣ X ; θ ) = ∏ i = 1 N [ h θ ( x ( i ) ) ] y ( i ) [ 1 − h θ ( x ( i ) ) ] ( 1 − y ( i ) ) P(Y|X;\space \theta) = \prod_{i=1}^N\space[h_{\theta}(x^{(i)})]^{y^{(i)}}\space[1 - h_{\theta}(x^{(i)})]^{(1- y^{(i)}\space )} P(Y∣X; θ)=i=1∏N [hθ(x(i))]y(i) [1−hθ(x(i))](1−y(i) )
理解LR模型内容引用自博客。
二、LR模型参数估计
梯度下降求解最优参数
极大似然估计:什么样的参数才能使我们观测到目前这组数据的概率最大。参数在整个样本空间的似然函数可表示为:
L ( θ ) = ∏ i = 1 N [ h θ ( x ( i ) ) ] y ( i ) [ 1 − h θ ( x ( i ) ) ] ( 1 − y ( i ) ) L(\theta) = \prod_{i=1}^N\space[h_{\theta}(x^{(i)})]^{y^{(i)}}\space[1 - h_{\theta}(x^{(i)})]^{(1- y^{(i)}\space )} L(θ)=i=1∏N [hθ(x(i))]y(i) [1−hθ(x(i))](1−y(i) )
则有对数似然函数 l ( θ ) l(\theta) l(θ):
l ( θ ) = ∑ i = 1 N [ y ( i ) l o g h θ ( x ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ] l(\theta) = \sum_{i=1}^N\space [y^{(i)}log\space h_{\theta}(x^{(i)}) + (1- y^{(i)})log(1 - h_{\theta}(x^{(i)}))] l(θ)=i=1∑N [y(i)log hθ(x(i))+(1−y(i))log(1−hθ(x(i)))]
函数从抽象到具体:
h θ ( x ) = s i g m o i d ( z ) = 1 1 + e − z h_{\theta}(x) = sigmoid(z) = \dfrac{1}{1+ e^{-z}} hθ(x)=sigmoid(z)=1+e−z1
z = w ⋅ x + b (3) z = w\cdot x + b \tag 3 z=w⋅x+b(3)
则有:
h θ ′ ( x ) = h θ ( x ) ( 1 − h θ ( x ) ) (4) {h_{\theta}}\prime(x) = h_{\theta}(x)(1-h_{\theta}(x)) \tag 4 hθ′(x)=hθ(x)(1−hθ(x))(4)
把求最大值问题转化为求最小值问题,即把求解似然函数最大值转化为求交叉熵损失函数最小值,则令:
J = − 1 N l ( θ ) = − 1 N ∑ i = 1 N [ y ( i ) l o g h θ ( x ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ] J = -\dfrac{1}{N}l(\theta) = -\dfrac{1}{N}\sum_{i=1}^N\space [y^{(i)}log\space h_{\theta}(x^{(i)}) + (1- y^{(i)})log(1 - h_{\theta}(x^{(i)}))] J=−N1l(θ)=−N1i=1∑N [y(i)log hθ(x(i))+(1−y(i))log(1−hθ(x(i)))]
则有:
∂ J ∂ h θ ( x ( i ) ) = − 1 N ∑ i = 1 N [ y ( i ) h θ ( x ( i ) ) − 1 − y ( i ) 1 − h θ ( x ( i ) ) ] (5) \dfrac{\partial J}{\partial h_{\theta}(x^{(i)})} = -\dfrac{1}{N}\sum_{i=1}^N\space [\dfrac{y^{(i)}}{h_{\theta}(x^{(i)})} - \dfrac{1- y^{(i)}}{1 - h_{\theta}(x^{(i)})}]\tag 5 ∂hθ(x(i))∂J=−N1i=1∑N [hθ(x(i))y(i)−1−hθ(x(i))1−y(i)](5)
根据式(4)有:
∂ h θ ( x ( i ) ) ∂ z = h θ ( x ( i ) ) ( 1 − h θ ( x ( i ) ) ) (6) \dfrac{\partial h_{\theta}(x^{(i)})}{\partial z} = h_{\theta}(x^{(i)})(1-h_{\theta}(x^{(i)}))\tag 6 ∂z∂hθ(x(i))=hθ(x(i))(1−hθ(x(i)))(6)
根据式(3)有:
∂ z ∂ w = x ( i ) (7) \dfrac{\partial z}{\partial w} = x^{(i)} \tag 7 ∂w∂z=x(i)(7)
∂ z ∂ b = 1 (8) \dfrac{\partial z}{\partial b} = 1 \tag 8 ∂b∂z=1(8)
则根据上式(5)(6)(7)(8)有:
d w = ∂ J ∂ h θ ( x ( i ) ) ∂ h θ ( x ( i ) ) ∂ z ∂ z ∂ w = 1 N ∑ i = 1 N [ h θ ( x ( i ) ) − y ( i ) ] x ( i ) dw = \dfrac{\partial J}{\partial h_{\theta}(x^{(i)})} \dfrac{\partial h_{\theta}(x^{(i)})}{\partial z}\dfrac{\partial z}{\partial w} = \dfrac{1}{N}\sum_{i=1}^N\space[h_{\theta}(x^{(i)}) - y^{(i)}]x^{(i)} dw=∂hθ(x(i))∂J∂z∂hθ(x(i))∂w∂z=N1i=1∑N [hθ(x(i))−y(i)]x(i)
d b = ∂ J ∂ h θ ( x ( i ) ) ∂ h θ ( x ( i ) ) ∂ z ∂ z ∂ b = 1 N ∑ i = 1 N [ h θ ( x ( i ) ) − y ( i ) ] db = \dfrac{\partial J}{\partial h_{\theta}(x^{(i)})} \dfrac{\partial h_{\theta}(x^{(i)})}{\partial z}\dfrac{\partial z}{\partial b} = \dfrac{1}{N}\sum_{i=1}^N\space[h_{\theta}(x^{(i)}) - y^{(i)}] db=∂hθ(x(i))∂J∂z∂hθ(x(i))∂b∂z=N1i=1∑N [hθ(x(i))−y(i)]
使用梯度下降的方法,对参数进行更新:
w = w − α × d w w = w - \alpha\times dw w=w−α×dw
b = b − α × d b b = b - \alpha\times db b=b−α×db
- α \alpha α为学习率
多项逻辑斯谛回归(multi-nominal logistic regression model)
推广到多分类,假设离散型随机变量Y的取值集合是{1,2,…,K},那么多项LR模型是:
P ( Y = k ∣ x ) = e w k x 1 + ∑ k = 1 K − 1 e w k x , k = 1 , 2 , … , K − 1 P(Y = k|x) = \dfrac{e^{w_k\space x}}{1 + \sum_{k=1}^{K-1}e^{w_k\space x}},k=1,2,…,K-1 P(Y=k∣x)=1+∑k=1K−1ewk xewk x,k=1,2,…,K−1
P ( Y = K ∣ x ) = 1 1 + ∑ k = 1 K − 1 e w k x , k = 1 , 2 , … , K − 1 P(Y = K|x) = \dfrac{1}{1 + \sum_{k=1}^{K-1}e^{w_k\space x}},k=1,2,…,K-1 P(Y=K∣x)=1+∑k=1K−1ewk x1,k=1,2,…,K−1
softmax
P ( Y = k ∣ x ) = e z k ∑ k = 1 K e z k , k = 1 , 2 , … , K P(Y = k|x) = \dfrac{e^{z_k}}{\sum_{k=1}^K e^{z_k}},k = 1,2,…,K P(Y=k∣x)=∑k=1Kezkezk,k=1,2,…,K
三、最大熵模型
最大熵模型是指:在所有满足约束条件的概率模型集合中,熵最大的模型是最好的;可以证明,在没有其它约束条件时,均匀分布模型是最大熵模型。
例如:P(A)+P(B)=1,按照最大熵模型得到P(A)=P(B)=0.5,也就是均匀分布。
可以从物理学的角度来理解该模型:根据热力学第二定理,如果没有外力干扰,系统的熵值是趋于不断增加的。由此,在没有其它额外参考信息的情况下,选择熵值最大的模型是最可靠的,因为没有外在动力时,宇宙本来就是趋于无序的。
1、最大熵原理
最大熵原理是概率模型学习的一个准则。最大熵原理认为,学习概率模型时,在所有可能的概率模型(分布)中,熵最大的模型就是最好的模型。通常用约束条件来确定概率模型的集合,所以,最大熵原理也可以表述为在满足约束条件的模型集合中选取熵最大的模型。
2、最大熵模型的定义
假设分类模型是一个条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X),X表示输入,Y表示输出,这个模型表示的是对于给定的输入X,以条件概率 P ( Y ∣ X ) P(Y|X) P(Y∣X)输出Y。
给定一个训练数据集:
T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x N , y N ) } T = \{(x_1,y_1),(x_2,y_2),…,(x_N,y_N)\} T={(x1,y1),(x2,y2),…,(xN,yN)}
学习的目标是用最大熵原理选择最好的分类模型。首先考虑模型应满足的条件,给定训练数据集,可以确定联合分布 P ( X , Y ) P(X,Y) P(X,Y)的经验分布和边缘分布 P ( X ) P(X) P(X)的经验分布,分别以 P ~ ( X , Y ) \tilde{P}(X,Y) P~(X,Y)和 P ~ ( X ) \tilde{P}(X) P~(X)表示。有:
P ~ ( X = x , Y = y ) = v ( X = x , Y = y ) N \tilde{P}(X=x,Y=y) = \dfrac{v(X=x,Y=y)}{N} P~(X=x,Y=y)=Nv(X=x,Y=y)
P ~ ( X = x ) = v ( X = x ) N \tilde{P}(X=x) = \dfrac{v(X=x)}{N} P~(X=x)=Nv(X=x)
- v ( X = x , Y = y ) v(X=x,Y=y) v(X=x,Y=y)表示训练数据中样本 ( x , y ) (x,y) (x,y)出现的频数, v ( X = x ) v(X=x) v(X=x)表述训练数据中输入 x x\space x 出现的频数,N表示训练样本容量。
用特征函数 f ( x , y ) f(x,y) f(x,y)描述输入 x x\space x 和 输 出 y 输出y\space 输出y 之间的某一个事实。其定义是:
f ( x , y ) = { 1 , x 与 y 满 足 某 一 事 实 0 , o t h e r v a l u e s f(x,y)=\begin{cases} 1, & x与y满足某一事实\\ 0, & other\ values \end{cases} f(x,y)={1,0,x与y满足某一事实other values
特征函数 f ( x , y ) f(x,y) f(x,y)关于经验分布 P ~ ( X , Y ) \tilde{P}(X,Y) P~(X,Y)的期望值,用 E P ~ ( f ) E_{\tilde{P}}(f) EP~(f)表示。
E P ~ ( f ) = ∑ x , y P ~ ( x , y ) f ( x , y ) = ∑ x , y P ~ ( x ) P ~ ( y ∣ x ) f ( x , y ) E_{\tilde{P}}(f) = \sum_{x,y}\tilde{P}(x,y)f(x,y) = \sum_{x,y}\tilde{P}(x)\tilde{P}(y|x)f(x,y) EP~(f)=x,y∑P~(x,y)f(x,y)=x,y∑P~(x)P~(y∣x)f(x,y)
特征函数 f ( x , y ) f(x,y) f(x,y)关于模型 P ( Y ∣ X ) P(Y|X) P(Y∣X)与经验分布 P ~ ( X ) \tilde{P}(X) P~(X)的期望值,用 E P ( f ) E_{P}(f) EP(f)表示。
E P ( f ) = ∑ x , y P ~ ( x ) P ( y ∣ x ) f ( x , y ) E_{P}(f) = \sum_{x,y}\tilde{P}(x)P(y|x)f(x,y) EP(f)=x,y∑P~(x)P(y∣x)f(x,y)
特征函数可以理解为模型的某个特征的描述,这个特征可以与数据集x的某一个特征(维度)对应,也可以不是指数据集x的特征。但此时特征函数里面的x与概率里面的x是必须对应的,都为特征或者都为实例或者其他某个规律的描述。
如果模型能够获取训练数据中的信息,则经验条件概率 P ~ ( y ∣ x ) \tilde{P}(y|x) P~(y∣x)与条件概率 P ( y ∣ x ) P(y|x) P(y∣x)近似相等。那么就可以假设这两个期望值相等,即:
E P ~ ( f ) = E P ( f ) (9) E_{\tilde{P}}(f) = E_{P}(f)\tag 9 EP~(f)=EP(f)(9)
故有
∑ x , y P ~ ( x , y ) f ( x , y ) = ∑ x , y P ~ ( x ) P ( y ∣ x ) f ( x , y ) \sum_{x,y}\tilde{P}(x,y)f(x,y) = \sum_{x,y}\tilde{P}(x)P(y|x)f(x,y) x,y∑P~(x,y)f(x,y)=x,y∑P~(x)P(y∣x)f(x,y)
将式(9)作为模型学习的约束,假如有n个特征函数 f i ( x , y ) , i = 1 , 2 , … , n f_i(x,y),i=1,2,…,n fi(x,y),i=1,2,…,n,那么就有n个约束条件。
C ≡ { P ∈ P ∣ E P ( f i ) = E P ~ ( f i ) , i = 1 , 2 , … , n } {C} \equiv \{P\in { P}|E_{P}(f_i) = E_{\tilde{P}}(f_i) ,i=1,2,…,n \} C≡{P∈P∣EP(fi)=EP~(fi),i=1,2,…,n}
定义在条件概率分布 P ( Y ∣ X ) P(Y | X) P(Y∣X)上的条件熵为:
H ( P ) = − ∑ x , y P ~ ( x ) P ( y ∣ x ) l o g P ( y ∣ x ) H(P)=−\sum_{x,y}\tilde{P}(x) P(y | x)logP(y | x) H(P)=−x,y∑P~(x)P(y∣x)logP(y∣x)
则模型集合 C {\bf C} C中条件熵 H ( P ) H(P) H(P)最大的模型称为最大熵模型。式中的对数为自然对数。
3、最大熵模型的学习
(1)定义问题
最大熵模型的学习等价于以下约束最优化问题:
m a x P ∈ C H ( P ) = − ∑ x , y P ~ ( x ) P ( y ∣ x ) l o g P ( y ∣ x ) max_{P\in{C}}\space\space H(P)=−\sum_{x,y}\tilde{P}(x) P(y | x)logP(y | x) maxP∈C H(P)=−x,y∑P~(x)P(y∣x)logP(y∣x)
s . t . E P ( f i ) = E P ~ ( f i ) , i = 1 , 2 , . . . , n s.t.\space\space E_P(f_i)=E_{\tilde{P}}(f_i), i=1,2,...,n s.t. EP(fi)=EP~(fi),i=1,2,...,n
∑ y P ( y ∣ x ) = 1 \sum_yP(y | x)=1 y∑P(y∣x)=1
按照最优化问题的习惯,将求最大值问题改写为等价的求最小值问题:
m i n P ∈ C − H ( P ) = ∑ x , y P ~ ( x ) P ( y ∣ x ) l o g P ( y ∣ x ) (10) min_{P\in{ C}}\space\space -H(P)=\sum_{x,y}\tilde{P}(x) P(y | x)logP(y | x)\tag {10} minP∈C −H(P)=x,y∑P~(x)P(y∣x)logP(y∣x)(10)
s . t . E P ~ ( f i ) − E P ( f i ) = 0 , i = 1 , 2 , . . . , n (11) s.t.\space\space E_{\tilde{P}}(f_i) - E_P(f_i)=0, i=1,2,...,n \tag {11} s.t. EP~(fi)−EP(fi)=0,i=1,2,...,n(11)
∑ y P ( y ∣ x ) = 1 (12) \sum_yP(y | x)=1 \tag {12} y∑P(y∣x)=1(12)
求解约束最优化问题(10)-(12),定义拉格朗日函数 L ( P , w ) L(P,w) L(P,w):
L ( w , p ) ≡ − H ( P ) + w 0 ( 1 − ∑ y P ( y ∣ x ) ) + ∑ i = 1 n w i ( E P ~ ( f i ) − E P ( f i ) ) = ∑ x , y P ~ ( x ) P ( y ∣ x ) l o g P ( y ∣ x ) + w 0 ( 1 − ∑ y P ( y ∣ x ) ) + ∑ i = 1 n w i ( ∑ x , y P ~ ( x , y ) f i ( x , y ) − ∑ x , y P ~ ( x ) P ( y ∣ x ) f i ( x , y ) ) (13) L(w,p) \equiv -H(P) + w_0(1-\sum_yP(y | x)) + \sum_{i=1}^nw_i(E_{\tilde{P}}(f_i) - E_P(f_i))\\ =\sum_{x,y}\tilde{P}(x) P(y | x)logP(y | x) + w_0(1-\sum_yP(y | x)) + \sum_{i=1}^nw_i(\sum_{x,y}\tilde{P}(x,y)f_i(x,y) - \sum_{x,y}\tilde{P}(x)P(y|x)f_i(x,y) )\tag {13} L(w,p)≡−H(P)+w0(1−y∑P(y∣x))+i=1∑nwi(EP~(fi)−EP(fi))=x,y∑P~(x)P(y∣x)logP(y∣x)+w0(1−y∑P(y∣x))+i=1∑nwi(x,y∑P~(x,y)fi(x,y)−x,y∑P~(x)P(y∣x)fi(x,y))(13)
最优化的原始问题即含有参数 w w w的部分最大时整体最小时 − H ( p ) -H(p) −H(p)取得最小值为:
m i n P ∈ C m a x w L ( P , w ) (14) min_{P\in{\ C}}\space max_w\space L(P,w)\tag {14} minP∈ C maxw L(P,w)(14)
我们将最小最大化问题转化成它的对偶问题,即最大最小化问题,要进行这种转化需要满足 H ( P ) H(P) H(P)为凸函数,以及 1 − ∑ y P ( y ∣ x ) 1-\sum_yP(y | x) 1−∑yP(y∣x)和 ∑ i = 1 n w i ( E P ~ ( f i ) − E P ( f i ) ) \sum_{i=1}^nw_i(E_{\tilde{P}}(f_i) - E_P(f_i)) ∑i=1nwi(EP~(fi)−EP(fi))为仿射函数:
m a x w m i n P ∈ C L ( P , w ) (15) max_w\space min_{P\in{\bf C}}\space L(P,w) \tag {15} maxw minP∈C L(P,w)(15)
(2)求解对偶问题内部的极小化问题
首先求解对偶问题(15)内部的极小化问题 m i n P ∈ C L ( P , w ) min_{P\in {C}}\space\space L(P,w) minP∈C L(P,w),得到的函数是 w w\space w 的函数,将其记作:
ψ ( w ) = m i n P ∈ C L ( P , w ) = L ( P w , w ) (16) \psi(w)= min_{P\in { C}}\space L(P,w) = L(P_w,w) \tag{16} ψ(w)=minP∈C L(P,w)=L(Pw,w)(16)
ψ ( w ) \psi(w) ψ(w)即为对偶函数,将其解记为:
P w = a r g m i n P ∈ C L ( P , w ) = P w ( y ∣ x ) P_w=arg\space min_{P\in{ C}}\space L(P,w)=P_w(y | x) Pw=arg minP∈C L(P,w)=Pw(y∣x)
具体的是求 L ( P , w ) L(P,w) L(P,w)关于 P ( y ∣ x ) P(y|x) P(y∣x)的偏导数:
∂ L ( P , w ) ∂ P ( y ∣ x ) = ∑ x , y P ~ ( x ) ( l o g P ( y ∣ x ) + 1 ) − ∑ y w 0 − ∑ x , y ( P ~ ( x ) ∑ i = 1 n w i f i ( x , y ) ) = ∑ x , y P ~ ( x ) ( l o g P ( y ∣ x ) + 1 − w 0 − ∑ i = 1 n w i f i ( x , y ) ) \dfrac{\partial L(P,w)}{\partial P(y|x)} = \sum_{x,y}\tilde{P}(x)(logP(y|x)+1)−\sum_yw_0−\sum_{x,y}(\tilde{P}(x)\sum_{i=1}^nw_if_i(x,y))\\ = \sum_{x,y}\tilde{P}(x)(logP(y|x)+1−w_0−\sum_{i=1}^nw_if_i(x,y)) ∂P(y∣x)∂L(P,w)=x,y∑P~(x)(logP(y∣x)+1)−y∑w0−x,y∑(P~(x)i=1∑nwifi(x,y))=x,y∑P~(x)(logP(y∣x)+1−w0−i=1∑nwifi(x,y))
因为 ∑ x P ~ ( x ) = 1 \sum_x \tilde{P}(x) = 1 ∑xP~(x)=1,所以 ∑ y w 0 = ∑ x P ~ ( x ) ∑ y w 0 = ∑ x , y P ~ ( x ) w 0 \sum_yw_0 = \sum_x \tilde{P}(x)\sum_yw_0 = \sum_{x,y} \tilde{P}(x) w_0 ∑yw0=∑xP~(x)∑yw0=∑x,yP~(x)w0
令偏导数为0,在 P ~ ( x ) > 0 \tilde{P}(x)>0 P~(x)>0的情况下,可以解出 P ( y ∣ x ) P(y|x) P(y∣x)关于 w w\space w 的表达式如下:
P ( y ∣ x ) = e x p ( ∑ i = 1 n w i f i ( x , y ) + w 0 − 1 ) = e x p ( ∑ i = 1 n w i f i ( x , y ) ) e x p ( 1 − w 0 ) P(y|x) = exp{(\sum_{i=1}^n w_i\space f_i\space(x,y) + w_0 -1)}= \dfrac{exp({\sum_{i=1}^n w_i\space f_i\space(x,y)})}{exp({1- w_0})} P(y∣x)=exp(i=1∑nwi fi (x,y)+w0−1)=exp(1−w0)exp(∑i=1nwi fi (x,y))
由于 ∑ y P ( y ∣ x ) = 1 \sum_y P(y|x) = 1 ∑yP(y∣x)=1,得:
P w ( y ∣ x ) = 1 Z w ( x ) e x p ( ∑ i = 1 n w i f i ( x , y ) ) (17) P_w(y|x) = \dfrac{1}{Z_w(x)}exp({\sum_{i=1}^n w_i\space f_i(x,y)})\tag{17} Pw(y∣x)=Zw(x)1exp(i=1∑nwi fi(x,y))(17)
因为 ∑ y P ( y ∣ x ) = 1 \sum_y P(y|x) = 1 ∑yP(y∣x)=1可以消除 w 0 w_0 w0,即得到如下的规范化因子。
其中:
Z w ( x ) = e x p ( 1 − w 0 ) = ∑ y e x p ( ∑ i = 1 n w i f i ( x , y ) ) (18) Z_w(x) = exp({1-w_0})=\sum_y exp({\sum_{i=1}^n w_i\space f_i(x,y)})\tag{18} Zw(x)=exp(1−w0)=y∑exp(i=1∑nwi fi(x,y))(18)
Z w ( x ) Z_w(x) Zw(x)称为规范化因子, f i ( x , y ) f_i(x,y) fi(x,y)是特征函数, w i w_i wi是特征的权重。
由式(17)(18)表示的模型 P w = P w ( y ∣ x ) P_w = P_w(y|x) Pw=Pw(y∣x)就是最大熵模型。这里, w w\space w 是最大熵模型中的参数向量。此时条件概率模型与softmax非常类似。
(3)求解对偶问题的外部极大化问题
之后求解对偶问题外部的极大化问题 m a x w ψ ( w ) max_w\space \psi(w) maxw ψ(w)。将其解记作 w ∗ w^{*} w∗,即:
w ∗ = a r g m a x w ψ ( w ) = a r g m a x w L ( P w ( y ∣ x ) , w ) w^{*} = arg\space max_w\space \psi(w) = arg\space max_w\space L(P_w(y|x),w) w∗=arg maxw ψ(w)=arg maxw L(Pw(y∣x),w)
因为前面在求 P w ( y ∣ x ) P_w(y|x) Pw(y∣x),消除其中含有的 w 0 w_0 w0参数已经使用过 1 − ∑ y P ( y ∣ x ) = 0 1-\sum_yP(y | x) = 0 1−∑yP(y∣x)=0条件,所以肯定有 1 − ∑ y P w ( y ∣ x ) = 0 1-\sum_yP_w(y | x) = 0 1−∑yPw(y∣x)=0,由式(13)有:
L ( P w ( y ∣ x ) , w ) = ∑ x , y P ~ ( x ) P w ( y ∣ x ) l n P w ( y ∣ x ) + ∑ i = 1 n w i ( ∑ x , y P ~ ( x , y ) f i ( x , y ) − ∑ x , y P ~ ( x ) P w ( y ∣ x ) f i ( x , y ) ) = ∑ x , y P ~ ( x ) P w ( y ∣ x ) ( l n P w ( y ∣ x ) − ∑ i = 1 n w i f i ( x , y ) ) + ∑ x , y P ~ ( x , y ) ∑ i = 1 n w i f i ( x , y ) L(P_w(y|x),w) = \sum_{x,y}\tilde{P}(x) P_w(y|x)lnP_w(y|x) + \sum_{i=1}^nw_i(\sum_{x,y}\tilde{P}(x,y)f_i(x,y) - \sum_{x,y}\tilde{P}(x)P_w(y|x)f_i(x,y) )\\ =\sum_{x,y}\tilde{P}(x) P_w(y|x)(lnP_w(y|x) - \sum_{i=1}^nw_i\space f_i(x,y)) + \sum_{x,y}\tilde{P}(x,y)\sum_{i=1}^nw_i\space f_i(x,y) L(Pw(y∣x),w)=x,y∑P~(x)Pw(y∣x)lnPw(y∣x)+i=1∑nwi(x,y∑P~(x,y)fi(x,y)−x,y∑P~(x)Pw(y∣x)fi(x,y))=x,y∑P~(x)Pw(y∣x)(lnPw(y∣x)−i=1∑nwi fi(x,y))+x,y∑P~(x,y)i=1∑nwi fi(x,y)
又因为 l n P w ( y ∣ x ) = ∑ i = 1 n w i f i ( x , y ) − l n Z w ( x ) lnP_w(y|x) = \sum_{i=1}^n w_i\space f_i(x,y) - lnZ_w(x) lnPw(y∣x)=∑i=1nwi fi(x,y)−lnZw(x)和 ∑ y P w ( y ∣ x ) = 1 \sum_yP_w(y|x) = 1 ∑yPw(y∣x)=1,所以有:
L ( P w ( y ∣ x ) , w ) = ∑ x , y P ~ ( x ) P w ( y ∣ x ) ( − l n Z w ( x ) ) + ∑ x , y P ~ ( x , y ) ∑ i = 1 n w i f i ( x , y ) = ∑ x P ~ ( x ) ( − l n Z w ( x ) ) ∑ y P w ( y ∣ x ) + ∑ x , y P ~ ( x , y ) ∑ i = 1 n w i f i ( x , y ) = ∑ x , y P ~ ( x , y ) ∑ i = 1 n w i f i ( x , y ) − ∑ x P ~ ( x ) l n Z w ( x ) (19) L(P_w(y|x),w) = \sum_{x,y}\tilde{P}(x) P_w(y|x)(-lnZ_w(x)) + \sum_{x,y}\tilde{P}(x,y)\sum_{i=1}^nw_i\space f_i(x,y)\\ =\sum_x\tilde{P}(x)(-lnZ_w(x))\sum_y P_w(y|x) + \sum_{x,y}\tilde{P}(x,y)\sum_{i=1}^nw_i\space f_i(x,y)\\ = \sum_{x,y}\tilde{P}(x,y)\sum_{i=1}^nw_i\space f_i(x,y) - \sum_x\tilde{P}(x)lnZ_w(x) \tag{19} L(Pw(y∣x),w)=x,y∑P~(x)Pw(y∣x)(−lnZw(x))+x,y∑P~(x,y)i=1∑nwi fi(x,y)=x∑P~(x)(−lnZw(x))y∑Pw(y∣x)+x,y∑P~(x,y)i=1∑nwi fi(x,y)=x,y∑P~(x,y)i=1∑nwi fi(x,y)−x∑P~(x)lnZw(x)(19)
得到了需要极大化的式子:
m a x w ∑ x , y P ~ ( x , y ) ∑ i = 1 n w i f i ( x , y ) − ∑ x P ~ ( x ) l n Z w ( x ) (20) max_{w}\space \sum_{x,y}\tilde{P}(x,y)\sum_{i=1}^nw_i\space f_i(x,y) - \sum_x\tilde{P}(x)lnZ_w(x)\tag{20} maxw x,y∑P~(x,y)i=1∑nwi fi(x,y)−x∑P~(x)lnZw(x)(20)
(4)最大似然估计
训练数据得经验概率分布 P ~ ( X , Y ) \tilde{P}(X, Y) P~(X,Y),条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)的对数似然函数可以表示为:
L P ~ ( P w ) = l n ∏ x , y P ( y ∣ x ) P ~ ( x , y ) = ∑ x , y P ~ ( x , y ) l n P ( y ∣ x ) L_{\tilde{P}}(P_w) = ln\prod_{x,y}P(y|x)^{\tilde{P}(x,y)} = \sum_{x,y}\tilde{P}(x,y)lnP(y|x) LP~(Pw)=lnx,y∏P(y∣x)P~(x,y)=x,y∑P~(x,y)lnP(y∣x)
将式(17) P w ( y ∣ x ) P_w(y|x) Pw(y∣x)代入有:
∑ x , y P ~ ( x , y ) l n P ( y ∣ x ) = ∑ x , y P ~ ( x , y ) ∑ i = 1 n w i f i ( x , y ) − ∑ x , y P ~ ( x , y ) l n Z w ( x ) = ∑ x , y P ~ ( x , y ) ∑ i = 1 n w i f i ( x , y ) − ∑ x P ~ ( x ) l n Z w ( x ) (21) \sum_{x,y}\tilde{P}(x,y)lnP(y|x) = \sum_{x,y}\tilde{P}(x,y)\sum_{i=1}^nw_i\space f_i\space (x,y) - \sum_{x,y}\tilde{P}(x,y)lnZ_w(x)\\ = \sum_{x,y}\tilde{P}(x,y)\sum_{i=1}^nw_i\space f_i\space (x,y) - \sum_{x}\tilde{P}(x)lnZ_w(x)\tag{21} x,y∑P~(x,y)lnP(y∣x)=x,y∑P~(x,y)i=1∑nwi fi (x,y)−x,y∑P~(x,y)lnZw(x)=x,y∑P~(x,y)i=1∑nwi fi (x,y)−x∑P~(x)lnZw(x)(21)
(5)结论
显而易见 L P ~ ( P w ) = ψ ( w ) L_{\tilde{P}}(P_w)=\psi(w) LP~(Pw)=ψ(w),拉格朗日对偶问题外部的极大化得到的结果与极大似然得到的结果是一样的。这样,最大熵模型的学习问题转换为具体求解对数似然函数极大化或对偶函数极大化的问题。
P w ( y ∣ x ) = 1 Z w ( x ) e x p ( ∑ i = 1 n w i f i ( x , y ) ) P_w(y|x) = \dfrac{1}{Z_w(x)}exp({\sum_{i=1}^n w_i\space f_i(x,y)}) Pw(y∣x)=Zw(x)1exp(i=1∑nwi fi(x,y))
Z w ( x ) = ∑ y e x p ( ∑ i = 1 n w i f i ( x , y ) ) Z_w(x) = \sum_y exp({\sum_{i=1}^n w_i\space f_i(x,y)}) Zw(x)=y∑exp(i=1∑nwi fi(x,y))
上式并没有一个显式的解析解,因此需要借助于数值的方法。由于是一个光滑的凸函数,所以可以求解的方法很多。可以使用的方法有:
- 通用迭代尺度法(GIS: Generalized Iterative Scaling)。
- 改进的迭代尺度法(IIS: Improved Iterative Scaling)。
- 梯度下降算法
- 拟牛顿法(牛顿法)
其中,前两个方法是专门为最大熵模型而设计的,后两种方法为通用的算法。
4、LR、softmax和最大熵模型之间的关系
- Logistic回归是统计学习中的经典分类方法,可以用于二类分类也可以用于多类分类。
- 最大熵模型由最大熵原理推导出来,最大熵原理是概率模型学习或估计的一个准则,最大熵原理认为在所有可能的概率模型的集合中,熵最大的模型是最好的模型,最大熵模型也可以用于二类分类和多类分类。
- Logistic回归模型与最大熵模型都属于对数线性模型。
- 逻辑回归跟最大熵模型没有本质区别。逻辑回归是最大熵对应类别为二类时的特殊情况
- 指数簇分布的最大熵等价于其指数形式的最大似然。
- 二项式分布的最大熵解等价于二项式指数形式(sigmoid)的最大似然;
- 多项式分布的最大熵等价于多项式分布指数形式(softmax)的最大似然。
5、最大熵模型和决策树模型的比对分析
粗看起来,上述模型似乎与在决策树中选用信息增益最大的特征参量有点儿矛盾。因为信息增益最大,即意味着要得到熵最小的模型。
两个模型中关于熵的定义完全一样,均用来表征模型的有序程度。熵值越大,越是无序。但两个模型其实并不矛盾,理由如下:
-
二者应用的前提不同。对于最大熵模型而言,在所有满足约束条件的模型中,如果没有其他的参考信息,则选用熵最大的模型;而决策树模型中,由于提供了特征参量这样的额外参考信息,因此不能直接应用最大熵原理。
-
决策树并没有使用最小熵模型。我们都知道,完全生长决策树的熵是最小的,然而却常常不是最好的模型(容易“过拟合”),经过剪枝后的决策树反而能够反映真实数据分布。如果说树的分裂意味着熵的减小,则剪枝意味着熵的增加;这样看来,我们选择的其实是应用了所有已知信息之后熵较大的模型。
-
决策树的思路是尽可能去拟合数据,然后加剪枝减少过拟合。
-
最大熵模型是先给你均匀分布,然后挖掘数据集里面隐含的约束条件来重新构造分布,使用的约束条件少就会欠拟合。决策树里面首先会选择信息增益最大的轴和切分点来切分,如果在最大熵模型里面也加上这个约束,然后依次对应起来。如果模型其中之一预测的精度比较高,那么最终两个模型的预测结果会非常接近。
最大熵原理:承认已知事物(知识);对未知事物不做任何假设,没有任何偏见。
两个角度认识未知事物:
- 最大熵模型:对不确定度的无偏分配;
- 最大似然估计:对知识的无偏理解。
参考资料:
- 统计学习方法–李航
- 最大熵模型 推导
- 最大熵模型(Maximum Entropy)
- 逻辑斯谛回归&最大熵模型
四、模型学习的最优化方法
1、改进的迭代尺度法(IIS)
改进的迭代尺度法(improved iterative scaling,IIS)是一种最大熵模型学习的最优化算法。
已知最大熵模型为:
P w ( y ∣ x ) = 1 Z w ( x ) e x p ( ∑ i = 1 n w i f i ( x , y ) ) (22) P_w(y|x) = \dfrac{1}{Z_w(x)}exp({\sum_{i=1}^n w_i\space f_i(x,y)})\tag{22} Pw(y∣x)=Zw(x)1exp(i=1∑nwi fi(x,y))(22)
Z w ( x ) = ∑ y e x p ( ∑ i = 1 n w i f i ( x , y ) ) (23) Z_w(x) = \sum_y exp({\sum_{i=1}^n w_i\space f_i(x,y)})\tag{23} Zw(x)=y∑exp(i=1∑nwi fi(x,y))(23)
f ( x , y ) = { 1 , x 与 y 满 足 某 一 事 实 0 , o t h e r v a l u e s f(x,y)=\begin{cases} 1, & x与y满足某一事实\\ 0, & other\ values \end{cases} f(x,y)={1,0,x与y满足某一事实other values
根据式(21)对数似然函数为:
L P ~ ( w ) = ∑ x , y P ~ ( x , y ) ∑ i = 1 n w i f i ( x , y ) − ∑ x P ~ ( x ) l n Z w ( x ) (24) L_{\tilde{P}}(w) = \sum_{x,y}\tilde{P}(x,y)\sum_{i=1}^nw_i\space f_i\space (x,y) - \sum_{x}\tilde{P}(x)lnZ_w(x)\tag{24} LP~(w)=x,y∑P~(x,y)i=1∑nwi fi (x,y)−x∑P~(x)lnZw(x)(24)
这里我们可以看到 L P ~ ( w ) ≤ 0 L_{\tilde{P}}(w)\leq 0 LP~(w)≤0,所以 L P ~ ( w ) = 0 L_{\tilde{P}}(w) = 0 LP~(w)=0是最优的。
给定特征集 { f 1 , f 2 , … , f n } \{ f_1,f_2,…,f_n\} {f1,f2,…,fn},最大熵模型式(22)和经验分布 P ~ ( x , y ) \tilde{P}(x,y) P~(x,y),要求:
W ∗ ≡ a r g m a x w L P ~ ( w ) W^* \equiv arg\space max_w\space L_{\tilde{P}}(w) W∗≡arg maxw LP~(w)
将式(23)代入式(24)得:
L P ~ ( w ) = ∑ x , y P ~ ( x , y ) ∑ i = 1 n w i f i ( x , y ) − ∑ x P ~ ( x ) ∑ y e x p ( ∑ i = 1 n w i f i ( x , y ) ) L_{\tilde{P}}(w) = \sum_{x,y}\tilde{P}(x,y)\sum_{i=1}^nw_i\space f_i\space (x,y) - \sum_{x}\tilde{P}(x)\sum_y exp({\sum_{i=1}^n w_i\space f_i(x,y)}) LP~(w)=x,y∑P~(x,y)i=1∑nwi fi (x,y)−x∑P~(x)y∑exp(i=1∑nwi fi(x,y))
对 w i w_i wi求偏导得:
∂ L P ~ ( w ) ∂ w i = ∑ x , y P ~ ( x , y ) f i ( x , y ) − ∑ x P ~ ( x ) P w ( y ∣ x ) f i ( x , y ) \dfrac{\partial L_{\tilde{P}}(w)}{\partial w_i} = \sum_{x,y}\tilde{P}(x,y)f_i\space (x,y) - \sum_{x}\tilde{P}(x)P_w(y|x)f_i\space (x,y) ∂wi∂LP~(w)=x,y∑P~(x,y)fi (x,y)−x∑P~(x)Pw(y∣x)fi (x,y)
令导数等于0得:
∑ x , y P ~ ( x , y ) f i ( x , y ) = ∑ x P ~ ( x ) P w ( y ∣ x ) f i ( x , y ) \sum_{x,y}\tilde{P}(x,y)f_i\space (x,y) = \sum_{x}\tilde{P}(x)P_w(y|x)f_i\space (x,y) x,y∑P~(x,y)fi (x,y)=x∑P~(x)Pw(y∣x)fi (x,y)
如果模型能够获取训练数据中的信息,上式是一个必然成立的条件,也就是式(9)假设的两个期望相等 E P ~ ( f ) = E P ( f ) E_{\tilde{P}}(f) = E_{P}(f) EP~(f)=EP(f)。
改进的迭代尺度法(IIS)思路:
假设最大熵模型当前的参数向量是 w = ( w 1 , w 2 , … , W n ) T w = (w_1,w_2,…,W_n)^T w=(w1,w2,…,Wn)T,我们希望找到一个新的参数向量 w + δ = ( w 1 + δ 1 , w 2 + δ 2 , … , w n + δ n ) T w +\delta = (w_1 +\delta_1,w_2 +\delta_2,…,w_n +\delta_n)^T w+δ=(w1+δ1,w2+δ2,…,wn+δn)T,使得模型的对数似然函数值增大。如果能有一种向量的更新方法 τ : w → w + δ \space \tau:w\rightarrow w + \delta τ:w→w+δ,那么就可以重复使用这一方法直接找到对数似然函数的最大值。
根据式(24)得:
L P ~ ( w + δ ) − L P ~ ( w ) = ∑ x , y P ~ ( x , y ) ∑ i = 1 n ( w i + δ i − w i ) f i ( x , y ) − ∑ x P ~ ( x ) l n Z w + δ ( x ) + ∑ x P ~ ( x ) l n Z w ( x ) = ∑ x , y P ~ ( x , y ) ∑ i = 1 n δ i f i ( x , y ) − ∑ x P ~ ( x ) l n Z w + δ ( x ) z w ( x ) L_{\tilde{P}}(w + \delta) - L_{\tilde{P}}(w) = \sum_{x,y}\tilde{P}(x,y)\sum_{i=1}^n(w_i + \delta_i - w_i)f_i\space (x,y) - \sum_{x}\tilde{P}(x)lnZ_{w+\delta}(x) + \sum_{x}\tilde{P}(x)lnZ_{w}(x) = \sum_{x,y}\tilde{P}(x,y)\sum_{i=1}^n \delta_i f_i\space (x,y) - \sum_{x}\tilde{P}(x)ln\dfrac{Z_{w+\delta}(x)}{z_w(x)} LP~(w+δ)−LP~(w)=x,y∑P~(x,y)i=1∑n(wi+δi−wi)fi (x,y)−x∑P~(x)lnZw+δ(x)+x∑P~(x)lnZw(x)=x,y∑P~(x,y)i=1∑nδifi (x,y)−x∑P~(x)lnzw(x)Zw+δ(x)
利用不等式: − l o g α ≥ 1 − α , ( α > 0 ) -log\alpha \geq 1-\alpha,(\alpha>0) −logα≥1−α,(α>0)
L P ~ ( w + δ ) − L P ~ ( w ) ≥ ∑ x , y P ~ ( x , y ) ∑ i = 1 n δ i f i ( x , y ) + ∑ x P ~ ( x ) − ∑ x P ~ ( x ) Z w + δ ( x ) z w ( x ) L_{\tilde{P}}(w + \delta) - L_{\tilde{P}}(w) \geq \sum_{x,y}\tilde{P}(x,y)\sum_{i=1}^n \delta_i f_i\space (x,y) + \sum_{x}\tilde{P}(x) - \sum_{x}\tilde{P}(x)\dfrac{Z_{w+\delta}(x)}{z_w(x)} LP~(w+δ)−LP~(w)≥x,y∑P~(x,y)i=1∑nδifi (x,y)+x∑P~(x)−x∑P~(x)zw(x)Zw+δ(x)
因为 ∑ x P ~ ( x ) = 1 \sum_{x}\tilde{P}(x) = 1 ∑xP~(x)=1,则有:
L P ~ ( w + δ ) − L P ~ ( w ) ≥ ∑ x , y P ~ ( x , y ) ∑ i = 1 n δ i f i ( x , y ) + 1 − ∑ x P ~ ( x ) Z w + δ ( x ) z w ( x ) L_{\tilde{P}}(w + \delta) - L_{\tilde{P}}(w) \geq \sum_{x,y}\tilde{P}(x,y)\sum_{i=1}^n \delta_i f_i\space (x,y) + 1 - \sum_{x}\tilde{P}(x)\dfrac{Z_{w+\delta}(x)}{z_w(x)} LP~(w+δ)−LP~(w)≥x,y∑P~(x,y)i=1∑nδifi (x,y)+1−x∑P~(x)zw(x)Zw+δ(x)
又因为:
Z w + δ ( x ) Z w ( x ) = 1 Z w ( x ) ∑ y e x p ( ∑ i = 1 n ( w i + δ i ) f i ( x , y ) ) = ∑ y 1 Z w ( x ) e x p ( ∑ i = 1 n w i f i ( x , y ) ) e x p ( ∑ i = 1 n δ i f i ( x , y ) ) = ∑ y P w ( y ∣ x ) e x p ( ∑ i = 1 n δ i f i ( x , y ) ) \dfrac{Z_{w+\delta}(x)}{Z_{w}(x)} = \dfrac{1}{Z_{w}(x)}\sum_y exp(\sum_{i=1}^n(w_i + \delta_i)f_i(x,y)) \\ = \sum_y\dfrac{1}{Z_{w}(x)}exp(\sum_{i=1}^n w_i f_i(x,y))exp(\sum_{i=1}^n \delta_i f_i(x,y))\\ =\sum_y P_w(y|x)exp(\sum_{i=1}^n \delta_i f_i(x,y)) Zw(x)Zw+δ(x)=Zw(x)1y∑exp(i=1∑n(wi+δi)fi(x,y))=y∑Zw(x)1exp(i=1∑nwifi(x,y))exp(i=1∑nδifi(x,y))=y∑Pw(y∣x)exp(i=1∑nδifi(x,y))
L P ~ ( w + δ ) − L P ~ ( w ) ≥ ∑ x , y P ~ ( x , y ) ∑ i = 1 n δ i f i ( x , y ) + 1 − ∑ x P ~ ( x ) ∑ y P w ( y ∣ x ) e x p ( ∑ i = 1 n δ i f i ( x , y ) ) L_{\tilde{P}}(w + \delta) - L_{\tilde{P}}(w) \geq \sum_{x,y}\tilde{P}(x,y)\sum_{i=1}^n \delta_i f_i\space (x,y) + 1 - \sum_{x}\tilde{P}(x)\sum_y P_w(y|x)exp(\sum_{i=1}^n \delta_i f_i(x,y)) LP~(w+δ)−LP~(w)≥x,y∑P~(x,y)i=1∑nδifi (x,y)+1−x∑P~(x)y∑Pw(y∣x)exp(i=1∑nδifi(x,y))
将右端记为:
A ( δ ∣ w ) = ∑ x , y P ~ ( x , y ) ∑ i = 1 n δ i f i ( x , y ) + 1 − ∑ x P ~ ( x ) ∑ y P w ( y ∣ x ) e x p ( ∑ i = 1 n δ i f i ( x , y ) ) (25) A(\delta|w) = \sum_{x,y}\tilde{P}(x,y)\sum_{i=1}^n \delta_i f_i\space (x,y) + 1 - \sum_{x}\tilde{P}(x)\sum_y P_w(y|x)exp(\sum_{i=1}^n \delta_i f_i(x,y))\tag {25} A(δ∣w)=x,y∑P~(x,y)i=1∑nδifi (x,y)+1−x∑P~(x)y∑Pw(y∣x)exp(i=1∑nδifi(x,y))(25)
L P ~ ( w + δ ) − L P ~ ( w ) ≥ A ( δ ∣ w ) L_{\tilde{P}}(w + \delta) - L_{\tilde{P}}(w) \geq A(\delta|w) LP~(w+δ)−LP~(w)≥A(δ∣w)
如果能找到适当的 δ \space \delta δ使下界 A ( δ ∣ w ) A(\delta|w) A(δ∣w)提高,那么似然函数也会提高,但是 A ( δ ∣ w ) A(\delta|w) A(δ∣w)是一个n维向量,不易于同时优化。IIS试图一次优化其中一个 δ i \delta_i δi,而固定其他 δ j \delta_j δj不变。为达到这一目的,并进一步降低下界,IIS引进新的量:
f # ( x , y ) = ∑ i f i ( x , y ) f^\#(x,y) = \sum_i f_i(x,y) f#(x,y)=i∑fi(x,y)
因为 f i ( x , y ) f_i(x,y) fi(x,y)是一个二值函数, f # ( x , y ) f^\#(x,y) f#(x,y)表示特征(x,y)出现的次数。这样可以重写式(25):
A ( δ ∣ w ) = ∑ x , y P ~ ( x , y ) ∑ i = 1 n δ i f i ( x , y ) + 1 − ∑ x P ~ ( x ) ∑ y P w ( y ∣ x ) e x p ( f # ( x , y ) ∑ i = 1 n δ i f i ( x , y ) f # ( x , y ) ) (26) A(\delta|w) = \sum_{x,y}\tilde{P}(x,y)\sum_{i=1}^n \delta_i f_i\space (x,y) + 1 - \sum_{x}\tilde{P}(x)\sum_y P_w(y|x)exp(\space f^\#(x,y)\sum_{i=1}^n\dfrac{\delta_if_i(x,y)}{f^\#(x,y)})\tag{26} A(δ∣w)=x,y∑P~(x,y)i=1∑nδifi (x,y)+1−x∑P~(x)y∑Pw(y∣x)exp( f#(x,y)i=1∑nf#(x,y)δifi(x,y))(26)
利用指数函数的凸函数性质,且 f i ( x , y ) f # ( x , y ) ≥ 0 \dfrac{f_i(x,y)}{f^\#(x,y)}\geq 0 f#(x,y)fi(x,y)≥0,使用Jensen不等式:
e x p ( ∑ x p ( x ) q ( x ) ) ≤ ∑ p ( x ) e x p ( q ( x ) ) exp(\sum_xp(x)q(x)) \leq \sum p(x)exp (q(x)) exp(x∑p(x)q(x))≤∑p(x)exp(q(x))
p ( x ) = f i ( x , y ) f # ( x , y ) p(x) = \dfrac{f_i(x,y)}{f^\#(x,y)} p(x)=f#(x,y)fi(x,y), q ( x ) = δ i f # ( x , y ) q(x) = \delta_i f^\#(x,y) q(x)=δif#(x,y)则有:
− e x p ( ∑ i = 1 n f i ( x , y ) f # ( x , y ) δ i f # ( x , y ) ) ≥ − ∑ i = 1 n f i ( x , y ) f # ( x , y ) e x p ( δ i f # ( x , y ) ) - exp(\sum_{i=1}^n\dfrac{f_i(x,y)}{f^\#(x,y)}\delta_if^\#(x,y)) \geq -\sum_{i=1}^n\dfrac{f_i(x,y)}{f^\#(x,y)}exp(\delta_i f^\#(x,y)) −exp(i=1∑nf#(x,y)fi(x,y)δif#(x,y))≥−i=1∑nf#(x,y)fi(x,y)exp(δif#(x,y))
所以:
A ( δ ∣ w ) ≥ ∑ x , y P ~ ( x , y ) ∑ i = 1 n δ i f i ( x , y ) + 1 − ∑ x P ~ ( x ) ∑ y P w ( y ∣ x ) ∑ i = 1 n ( f i ( x , y ) f # ( x , y ) ) e x p ( δ i f # ( x , y ) ) A(\delta|w) \geq \sum_{x,y}\tilde{P}(x,y)\sum_{i=1}^n \delta_i f_i\space (x,y) + 1 - \sum_{x}\tilde{P}(x)\sum_y P_w(y|x)\sum_{i=1}^n(\dfrac{f_i(x,y)}{f^\#(x,y)})exp({\delta_i f^\#(x,y)}) A(δ∣w)≥x,y∑P~(x,y)i=1∑nδifi (x,y)+1−x∑P~(x)y∑Pw(y∣x)i=1∑n(f#(x,y)fi(x,y))exp(δif#(x,y))
不等式右边记为:
B ( δ ∣ w ) = ∑ x , y P ~ ( x , y ) ∑ i = 1 n δ i f i ( x , y ) + 1 − ∑ x P ~ ( x ) ∑ y P w ( y ∣ x ) ∑ i = 1 n ( f i ( x , y ) f # ( x , y ) ) e x p ( δ i f # ( x , y ) ) B(\delta|w) = \sum_{x,y}\tilde{P}(x,y)\sum_{i=1}^n \delta_i f_i\space (x,y) + 1 - \sum_{x}\tilde{P}(x)\sum_y P_w(y|x)\sum_{i=1}^n(\dfrac{f_i(x,y)}{f^\#(x,y)})exp({\delta_i f^\#(x,y)}) B(δ∣w)=x,y∑P~(x,y)i=1∑nδifi (x,y)+1−x∑P~(x)y∑Pw(y∣x)i=1∑n(f#(x,y)fi(x,y))exp(δif#(x,y))
所以:
L P ~ ( w + δ ) − L P ~ ( w ) ≥ B ( δ ∣ w ) L_{\tilde{P}}(w + \delta) - L_{\tilde{P}}(w) \geq B(\delta|w) LP~(w+δ)−LP~(w)≥B(δ∣w)
对于新的下界 B ( δ ∣ w ) B(\delta|w) B(δ∣w),对 δ i \delta_i δi求偏导得:
∂ B ( δ ∣ w ) ∂ δ i = ∑ x , y P ~ ( x , y ) f i ( x , y ) − ∑ x P ~ ( x ) ∑ y P w ( y ∣ x ) f i ( x , y ) e x p ( δ i f # ( x , y ) ) \dfrac{\partial B(\delta|w)}{\partial \delta_i} = \sum_{x,y}\tilde{P}(x,y)f_i\space (x,y) - \sum_{x}\tilde{P}(x)\sum_y P_w(y|x)f_i\space (x,y)exp(\delta_i f^\#(x,y)) ∂δi∂B(δ∣w)=x,y∑P~(x,y)fi (x,y)−x∑P~(x)y∑Pw(y∣x)fi (x,y)exp(δif#(x,y))
令导数为0得:
∑ x P ~ ( x ) ∑ y P w ( y ∣ x ) f i ( x , y ) e x p ( δ i f # ( x , y ) ) = ∑ x , y P ~ ( x , y ) f i ( x , y ) \sum_{x}\tilde{P}(x)\sum_y P_w(y|x)f_i\space (x,y)exp(\delta_i f^\#(x,y)) = \sum_{x,y}\tilde{P}(x,y)f_i\space (x,y) x∑P~(x)y∑Pw(y∣x)fi (x,y)exp(δif#(x,y))=x,y∑P~(x,y)fi (x,y)
∑ x P ~ ( x ) ∑ y P w ( y ∣ x ) f i ( x , y ) e x p ( δ i f # ( x , y ) ) = E P ~ ( f i ) (27) \sum_{x}\tilde{P}(x)\sum_y P_w(y|x)f_i\space (x,y)exp(\delta_i f^{\#}(x,y)) = E_{\tilde{P}}(f_i) \tag{27} x∑P~(x)y∑Pw(y∣x)fi (x,y)exp(δif#(x,y))=EP~(fi)(27)
依次对 δ i \delta_i δi求解方程(27)从而求出 δ \delta δ
改进的迭代尺度算法IIS
输入:特征函数 f 1 , f 2 , … , f n f_1,f_2,…,f_n f1,f2,…,fn,经验分布 P ~ ( X , Y ) \tilde{P}(X,Y) P~(X,Y),模型 P w ( y ∣ x ) P_w(y|x) Pw(y∣x)
输出:最优参数值 w i ∗ w_i^{*} wi∗,最优模型 P w ∗ P_{w^{*}} Pw∗
(1)对所有 i ∈ { 1 , 2 , … , n } i\in \{1,2,…,n\} i∈{1,2,…,n},取初值 w i = 0 w_i = 0 wi=0
(2)对每一 i ∈ { 1 , 2 , … , n } i\in \{1,2,…,n\} i∈{1,2,…,n}:
(a) 令 δ i \delta_i δi是方程
∑ x P ~ ( x ) ∑ y P w ( y ∣ x ) f i ( x , y ) e x p ( δ i f # ( x , y ) ) = E P ~ ( f i ) \sum_{x}\tilde{P}(x)\sum_y P_w(y|x)f_i\space (x,y)exp(\delta_i f^{\#}(x,y)) = E_{\tilde{P}}(f_i) x∑P~(x)y∑Pw(y∣x)fi (x,y)exp(δif#(x,y))=EP~(fi)
的解,这里,
f # ( x , y ) = ∑ i = 1 n f i ( x , y ) f^\#(x,y) = \sum_{i=1}^n f_i(x,y) f#(x,y)=i=1∑nfi(x,y)
(b) 更新 w i w_i wi值: w i ← w i + δ i w_i \leftarrow w_i + \delta_i wi←wi+δi
(3)如果不是所有的 w i w_i wi都收敛,重复步骤(2)。
这一算法关键一步是(a),即求解方程(27)中的 δ i \delta_i δi。如果 f # ( x , y ) f^\#(x,y) f#(x,y)是常数,即对任何 x , y x,y x,y,有 f # ( x , y ) = M f^\#(x,y)=M f#(x,y)=M,那么 δ i \delta_i δi可以显示地表示成
δ i = 1 M l n E P ~ ( f i ) E P ( f i ) (28) \delta_i = \dfrac{1}{M}ln\dfrac{E_{\tilde{P}}(f_i)}{E_P(f_i)}\tag{28} δi=M1lnEP(fi)EP~(fi)(28)
如果 f # ( x , y ) f^\#(x,y) f#(x,y)不是常数,那么必须通过数值计算求 δ i \delta_i δi。简单有效的方法是牛顿法。以 g ( δ i ) = 0 g(\delta_i) = 0 g(δi)=0表示方程(27),牛顿法通过迭代求得 δ i ∗ \delta_i^{*} δi∗,使得 δ i ∗ = 0 \delta_i^{*}=0 δi∗=0,迭代的公式是
δ i ( k + 1 ) = δ i ( k ) − g ( δ i ( k ) ) g ′ ( δ i ( k ) ) (29) \delta_i^{(k+1)} = \delta_i^{(k)} - \dfrac{g(\delta_i^{(k)})}{g\prime(\delta_i^{(k)})}\tag{29} δi(k+1)=δi(k)−g′(δi(k))g(δi(k))(29)
只要适当选取初始值 δ i ( 0 ) \delta_i^{(0)} δi(0),由于 δ i \delta_i δi的方程(27)有单根,因此牛顿法恒收敛,而且收敛速度很快。
2、拟牛顿法
这一部分有些难度,公式能看懂,要是应用代码实现感觉还是有困难,后面再完善和补充吧!发明这算法的人牛逼。
参考资料:
- 统计学习方法—李航
- 改进的迭代尺度算法(IIS)总结
∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ **************************************** ∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗
未完待续!代码实例