数模（06）---模拟退火模型

模拟退火模型背景简介

        退火：退火是指将固体加热到足够高的温度，使分子呈随机排列状态，然后局部降温使之冷却，最后分子以低能状态排列，固体达到某种稳定状态。

        热力学中的退火现象：指物体逐渐降温时发生的物理现象。温度越低，物体的能量状态越低，到达足够的低点时，液体开始冷凝与结晶，在结晶状态时，系统的能量状态最低。缓慢降温时，可达到最低能量状态；但如果快速降温，会导致不是最低能量态的非晶体。

模拟退火算法思想

        利用了物体中固体物质的退火与一般优化问题的相似性从某一初始温度开始，伴随温度的不断下降，结合概率突跳特性在解空间中随机寻找全局最优解。

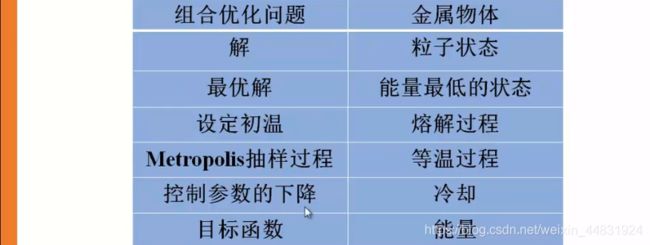
模拟退火算法简介

模拟退火算法对TSP问题的求解

        TSP问题：即Travelling Salesman Problem（旅行商问题）。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得到的路径为所有路径中的最小值。

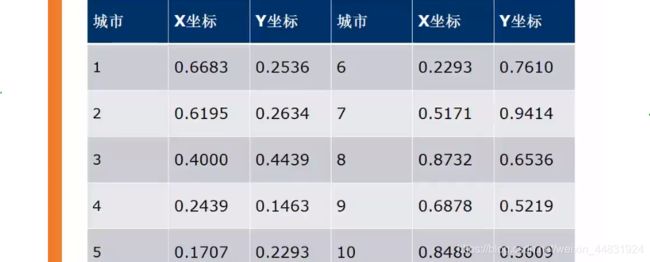
模拟退火模型matlab源码

• 根据上面提出的旅行商问题，下面编写matlab源码

swap.m

function [ newpath , position ] = swap( oldpath , number )
% 对 oldpath 进 行 互 换 操 作
% number 为 产 生 的 新 路 径 的 个 数
% position 为 对 应 newpath 互 换 的 位 置
m = length( oldpath ) ; % 城 市 的 个 数
newpath = zeros( number , m ) ;
position = sort( randi( m , number , 2 ) , 2 ); % 随 机 产 生 交 换 的 位 置
for i = 1 : number
    newpath( i , : ) = oldpath ;
    % 交 换 路 径 中 选 中 的 城 市
    newpath( i , position( i , 1 ) ) = oldpath( position( i , 2 ) ) ;
    newpath( i , position( i , 2 ) ) = oldpath( position( i , 1 ) ) ;
end

pathfare.m

function [ objval ] = pathfare( fare , path )
% 计 算 路 径 path 的 代 价 objval
% path 为 1 到 n 的 排 列 ，代 表 城 市 的 访 问 顺 序 ；
% fare 为 代 价 矩 阵 ， 且 为 方 阵 。
[ m , n ] = size( path ) ;
objval = zeros( 1 , m ) ;
for i = 1 : m
    for j = 2 : n
        objval( i ) = objval( i ) + fare( path( i , j - 1 ) , path( i , j ) ) ;
    end
    objval( i ) = objval( i ) + fare( path( i , n ) , path( i , 1 ) ) ;
end

distance.m

function [ fare ] = distance( coord )
% 根 据 各 城 市 的 距 离 坐 标 求 相 互 之 间 的 距 离
% fare 为 各 城 市 的 距 离 ， coord 为 各 城 市 的 坐 标
[ v , m ] = size( coord ) ; % m 为 城 市 的 个 数
fare = zeros( m ) ;
for i = 1 : m % 外 层 为 行
    for j = i : m % 内 层 为 列
        fare( i , j ) = ( sum( ( coord( : , i ) - coord( : , j ) ) .^ 2 ) ) ^ 0.5 ;
        fare( j , i ) = fare( i , j ) ; % 距 离 矩 阵 对 称
    end
end

myplot.m

function [ ] = myplot( path , coord , pathfar )
% 做 出 路 径 的 图 形
% path 为 要 做 图 的 路 径 ，coord 为 各 个 城 市 的 坐 标
% pathfar 为 路 径 path 对 应 的 费 用
len = length( path ) ;
clf ;
hold on ;
title( [ '近似最短路径如下，路程为' , num2str( pathfar ) ] ) ;
plot( coord( 1 , : ) , coord( 2 , : ) , 'ok');
pause( 0.4 ) ;
for ii = 2 : len
    plot( coord( 1 , path( [ ii - 1 , ii ] ) ) , coord( 2 , path( [ ii - 1 , ii ] ) ) , '-b');
    x = sum( coord( 1 , path( [ ii - 1 , ii ] ) ) ) / 2 ;
    y = sum( coord( 2 , path( [ ii - 1 , ii ] ) ) ) / 2 ;
    text( x , y , [ '(' , num2str( ii - 1 ) , ')' ] ) ;
    pause( 0.4 ) ;
end
plot( coord( 1 , path( [ 1 , len ] ) ) , coord( 2 , path( [ 1 , len ] ) ) , '-b' ) ;
x = sum( coord( 1 , path( [ 1 , len ] ) ) ) / 2 ;
y = sum( coord( 2 , path( [ 1 , len ] ) ) ) / 2 ;
text( x , y , [ '(' , num2str( len ) , ')' ] ) ;
pause( 0.4 ) ;
hold off ;

Tsp.m

clear;
% 程 序 参 数 设 定
Coord = ... % 城 市 的 坐 标 Coordinates
[ 0.6683 0.6195 0.4    0.2439 0.1707 0.2293 0.5171 0.8732 0.6878 0.8488 ; ...
  0.2536 0.2634 0.4439 0.1463 0.2293 0.761  0.9414 0.6536 0.5219 0.3609 ] ;
t0 = 1 ; % 初 温 t0
iLk = 20 ; % 内 循 环 最 大 迭 代 次 数 iLk
oLk = 50 ; % 外 循 环 最 大 迭 代 次 数 oLk
lam = 0.95 ; % λ lambda
istd = 0.001 ; % 若 内 循 环 函 数 值 方 差 小 于 istd 则 停 止
ostd = 0.001 ; % 若 外 循 环 函 数 值 方 差 小 于 ostd 则 停 止
ilen = 5 ; % 内 循 环 保 存 的 目 标 函 数 值 个 数
olen = 5 ; % 外 循 环 保 存 的 目 标 函 数 值 个 数
% 程 序 主 体
m = length( Coord ) ; % 城 市 的 个 数 m
fare = distance( Coord ) ; % 路 径 费 用 fare
path = 1 : m ; % 初 始 路 径 path
pathfar = pathfare( fare , path ) ; % 路 径 费 用 path fare
ores = zeros( 1 , olen ) ; % 外 循 环 保 存 的 目 标 函 数 值
e0 = pathfar ; % 能 量 初 值 e0
t = t0 ; % 温 度 t
for out = 1 : oLk % 外 循 环 模 拟 退 火 过 程
    ires = zeros( 1 , ilen ) ; % 内 循 环 保 存 的 目 标 函 数 值
    for in = 1 : iLk % 内 循 环 模 拟 热 平 衡 过 程
        [ newpath , v ] = swap( path , 1 ) ; % 产 生 新 状 态
        e1 = pathfare( fare , newpath ) ; % 新 状 态 能 量
        % Metropolis 抽 样 稳 定 准 则
        r = min( 1 , exp( - ( e1 - e0 ) / t ) ) ;
        if rand < r
            path = newpath ; % 更 新 最 佳 状 态
            e0 = e1 ;
        end
        ires = [ ires( 2 : end ) e0 ] ; % 保 存 新 状 态 能 量
        % 内 循 环 终 止 准 则 ：连 续 ilen 个 状 态 能 量 波 动 小 于 istd
        if std( ires , 1 ) < istd
            break ;
        end
    end
    ores = [ ores( 2 : end ) e0 ] ; % 保 存 新 状 态 能 量
    % 外 循 环 终 止 准 则 ：连 续 olen 个 状 态 能 量 波 动 小 于 ostd
    if std( ores , 1 ) < ostd
        break ;
    end
    t = lam * t ;
end
pathfar = e0 ;
% 输 入 结 果
fprintf( '近似最优路径为：\n ' )
% disp( char( [ path , path(1) ] + 64 ) ) ;
disp(path)
fprintf( '近似最优路径路程\tpathfare=' ) ;
disp( pathfar ) ;
myplot( path , Coord , pathfar ) ;

        注意：求相似的城市旅行商问题，需要修改程序时，就只要把TSP.m程序的城市坐标换一下即可。即Tsp文件中的coord，2行，第一行是x坐标，下面对应的是y坐标，记住x，y一定要对应起来，每次运行tsp的结果都不相同，因为他没有一个准确的答案，只是求出一个最优解。

         最后上面问题输出的结果为：

TSP“旅行商问题”的应用领域

        

1. 如何规划最合理高效的道路交通，以减少拥堵；
2. 如何更好的规划物流，以减少运营成本；
3. 在互联网环境中如何更好地设置节点，以更好地让信息流动等。