pytorch中的正则化-weight decay与dropout
**
首先是pytorch中的L2正则项weight decay
**
一.正则化与偏差方差分解
Regularization:减小方差的策略
误差可分解为:偏差,方差与噪声之和。即误差=偏差+方差+噪声之和
偏差度量了学习算法的期望预测与真实结果的偏离程度,即刻画了学习算法本身的拟合能力
方差度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响
噪声则表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界

L2正则化项等同于权值衰减,推导过程如下:

权值衰减实在优化器中实现的:
optim_normal = torch.optim.SGD(net_normal.parameters(), lr=lr_init, momentum=0.9)
optim_wdecay = torch.optim.SGD(net_weight_decay.parameters(), lr=lr_init, momentum=0.9, weight_decay=1e-2)
在runs所在目录下进入tensorboard:tensorboard --logdir=./runs
没有带L2正则化的,整个权值变化不大。
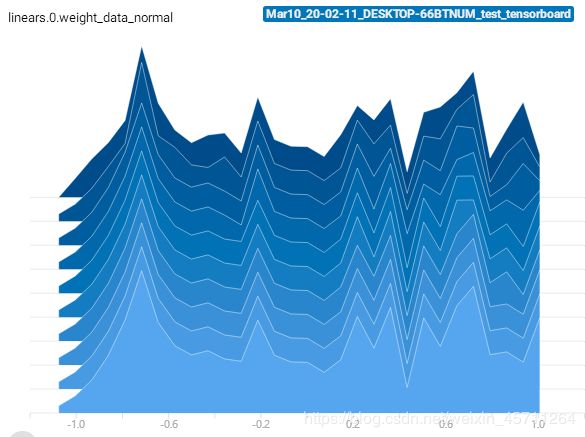
带L2正则化的,权值不断缩减。

在代码optim_wdecay.step()设置断点,并进入(step into)
在代码的d_p.add_(weight_decay, p.data)进行权值衰减。其公式是:d_p = d_p + p.data * weight_decay
在代码p.data.add_(-group['lr'], d_p)进行梯度更新。
再来谈谈dropout
dropout可以减轻过拟合,降低方差,还可以控制权重的范围(这类似于L2)。
Dropout:随机失活
随机:dropout probability
失活:weight = 0
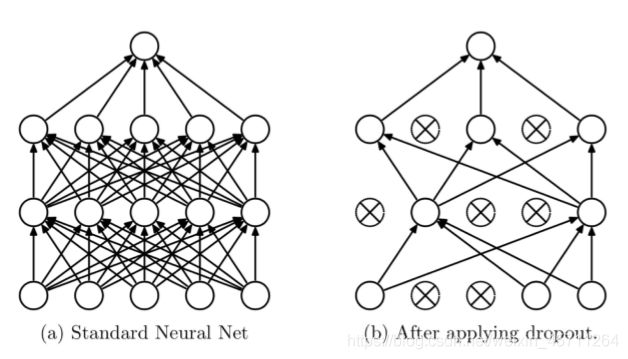
数据尺度变化:测试时,所有权重乘以1-drop_prob
如drop_prob = 0.3 , 1-drop_prob = 0.7
nn.Dropout 功能:
Dropout层 参数: • p:被舍弃概率,失活概率
实现细节: 训练时**权重均乘以 1/(1−)**先放大尺度,随机失活等于没放大,即除以1-p。这样测试时就不用再除以1-p了。降低了测试的复杂度,提高了测试的速度。
这里可以从数据尺度的角度理解,如果训练时不放大,相当于缩小为原来的(1-p)倍,训练的目标还是一样的。测试的时候,采用训练好的网络测试,相当于网络没缩小,数据量也没减少,数据尺度比原来大了,预测不准。
未加dropout的权重:
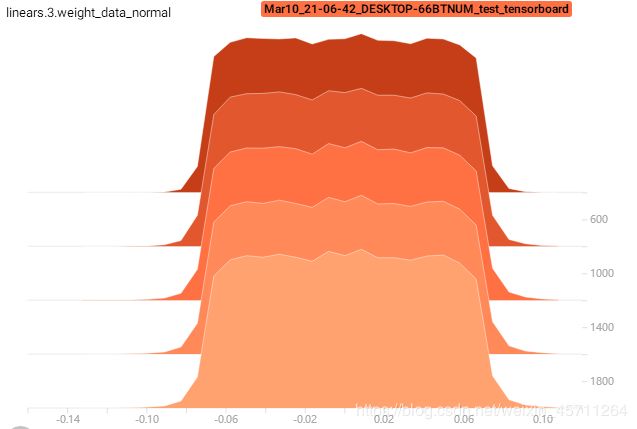
加了dropout的权重效果:
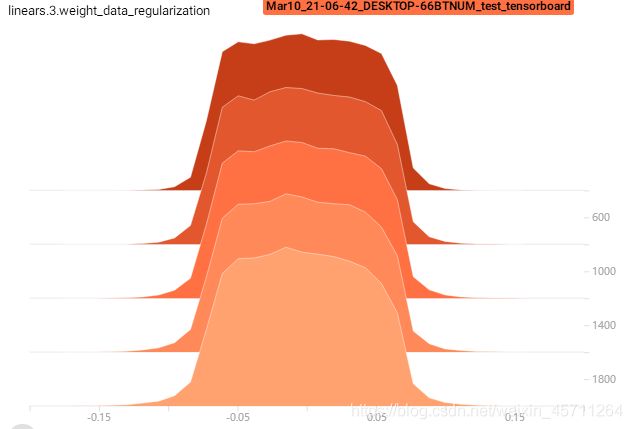
相当于加了之后,权重的范围受到了一定的限制,向0靠拢了。
dropout一般在需要dropout的那个网络层的前一层。并且通常输出层之前是不加dropout的,比较简单的网络可以加:
class MLP(nn.Module):
def __init__(self, neural_num, d_prob=0.5):
super(MLP, self).__init__()
self.linears = nn.Sequential(
nn.Linear(1, neural_num),
nn.ReLU(inplace=True),
nn.Dropout(d_prob),
nn.Linear(neural_num, neural_num),
nn.ReLU(inplace=True),
nn.Dropout(d_prob),
nn.Linear(neural_num, neural_num),
nn.ReLU(inplace=True),
nn.Dropout(d_prob),
nn.Linear(neural_num, 1),
)
在优化器中实现:
net_prob_0 = MLP(neural_num=n_hidden, d_prob=0.)
net_prob_05 = MLP(neural_num=n_hidden, d_prob=0.5)
# ============================ step 3/5 优化器 ============================
optim_normal = torch.optim.SGD(net_prob_0.parameters(), lr=lr_init, momentum=0.9)
optim_reglar = torch.optim.SGD(net_prob_05.parameters(), lr=lr_init, momentum=0.9)
这里注意:测试的时候是不采用dropout的。在如下的代码中,进行测试之前,先通过.eval()的方法调整为测试模式。快跳出测试之前,再用.train方法,转换为训练模式,使用dropout。
# ============================ step 5/5 迭代训练 ============================
writer = SummaryWriter(comment='_test_tensorboard', filename_suffix="12345678")
for epoch in range(max_iter):
pred_normal, pred_wdecay = net_prob_0(train_x), net_prob_05(train_x)
loss_normal, loss_wdecay = loss_func(pred_normal, train_y), loss_func(pred_wdecay, train_y)
optim_normal.zero_grad()
optim_reglar.zero_grad()
loss_normal.backward()
loss_wdecay.backward()
optim_normal.step()
optim_reglar.step()
if (epoch+1) % disp_interval == 0:
net_prob_0.eval()
net_prob_05.eval()
# 可视化
for name, layer in net_prob_0.named_parameters():
writer.add_histogram(name + '_grad_normal', layer.grad, epoch)
writer.add_histogram(name + '_data_normal', layer, epoch)
for name, layer in net_prob_05.named_parameters():
writer.add_histogram(name + '_grad_regularization', layer.grad, epoch)
writer.add_histogram(name + '_data_regularization', layer, epoch)
test_pred_prob_0, test_pred_prob_05 = net_prob_0(test_x), net_prob_05(test_x)
# 绘图
plt.scatter(train_x.data.numpy(), train_y.data.numpy(), c='blue', s=50, alpha=0.3, label='train')
plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='red', s=50, alpha=0.3, label='test')
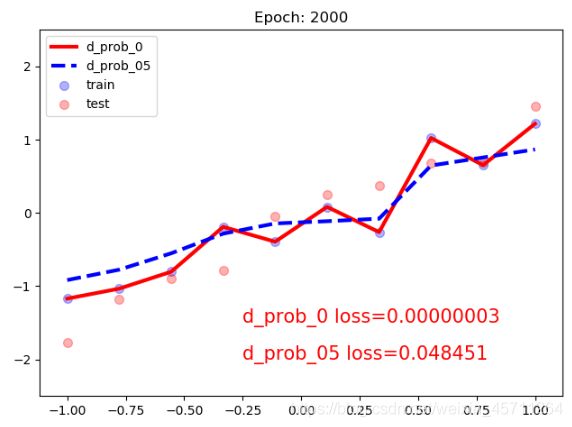
plt.plot(test_x.data.numpy(), test_pred_prob_0.data.numpy(), 'r-', lw=3, label='d_prob_0')
plt.plot(test_x.data.numpy(), test_pred_prob_05.data.numpy(), 'b--', lw=3, label='d_prob_05')
plt.text(-0.25, -1.5, 'd_prob_0 loss={:.8f}'.format(loss_normal.item()), fontdict={'size': 15, 'color': 'red'})
plt.text(-0.25, -2, 'd_prob_05 loss={:.6f}'.format(loss_wdecay.item()), fontdict={'size': 15, 'color': 'red'})
plt.ylim((-2.5, 2.5))
plt.legend(loc='upper left')
plt.title("Epoch: {}".format(epoch+1))
plt.show()
plt.close()
net_prob_0.train()
net_prob_05.train()