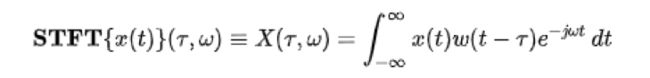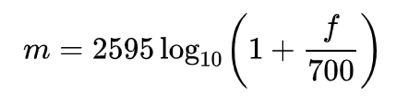如何将机器学习和深度学习方法应用到音频分析中

要查看代码、培训可视化以及本文末尾有关python示例的更多信息，请访问Comet项目页面 。

介绍

尽管有关深度学习的许多著作和文献都涉及计算机视觉和自然语言处理（NLP） ，但是音频分析（包括自动语音识别（ASR） ，数字信号处理以及音乐分类、标记和生成的领域）是一项深度学习应用程序的不断增长的子域。 虚拟助手Alexa、Siri和Google Home是一些最流行和广泛使用的机器学习系统，它们主要是基于模型构建的产品，可以从音频信号中提取信息。

Comet的许多用户都在从事与音频相关的机器学习任务，例如音频分类、语音识别和语音合成，因此我们使用Comet的元机器学习平台为他们构建了分析，探索和理解音频数据的工具。

使用 Comet进行 音频建模、培训和调试

这篇文章的重点是展示数据科学家和AI从业人员如何使用Comet在音频分析领域应用机器学习和深度学习方法。 为了了解模型如何从数字音频信号中提取信息，我们将深入研究音频分析的一些核心特征工程方法。

然后，我们将使用Librosa （一个用于音频分析的出色python库）来编写一个简短的Python示例，训练UrbanSound8k数据集上的神经体系结构。

音频的机器学习：数字信号处理、滤波器组、梅尔频率倒谱系数

建立机器学习模型以分类、描述或生成音频通常涉及建模任务，其中输入数据是音频样本。

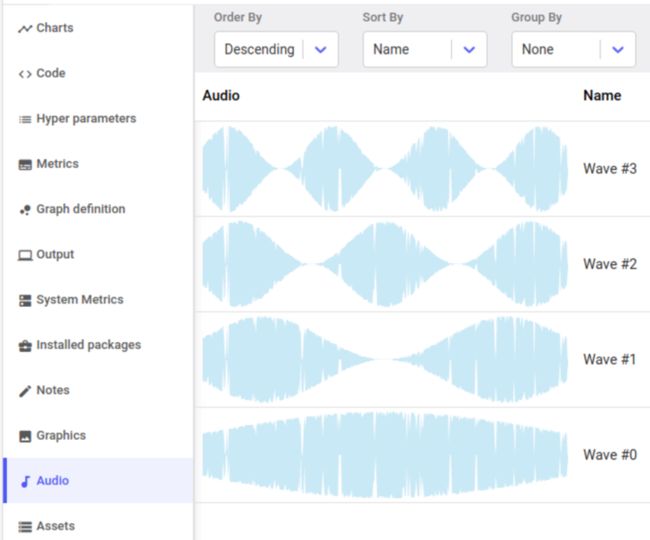
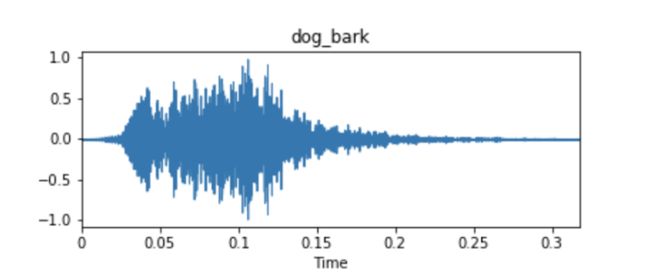
来自UrbanSound8k的音频数据集样本的示例波形

这些音频样本通常表示为时间序列，其中y轴测量值是波形的幅度。 通常根据最初拾取音频的麦克风或接收器设备周围的压力变化来测量振幅。 除非有与音频样本相关联的元数据，否则这些时间序列信号通常将是您唯一用于拟合模型的输入数据。

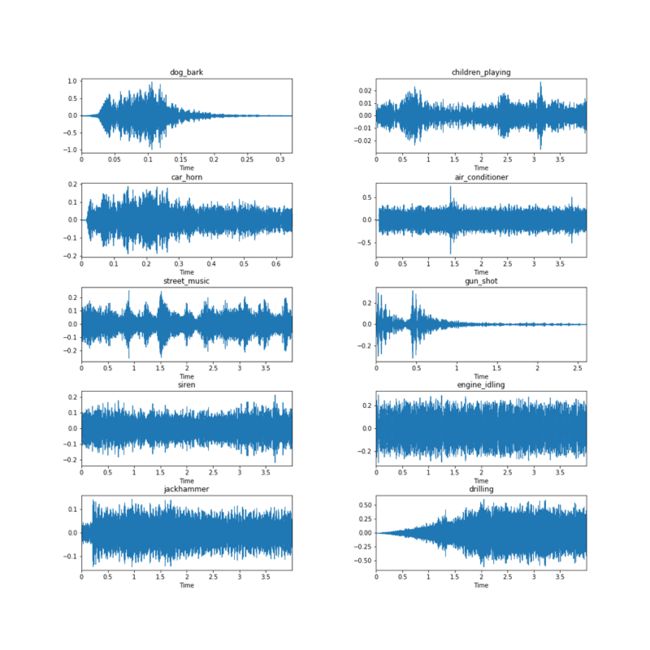
查看下面的样本，这些样本取自Urbansound8k数据集中的十个类别中的每个类别，从眼图测试可以清楚地看出，波形本身不一定可以产生清晰的类别标识信息。 考虑一下engine_idling，siren和jackhammer类的波形，它们看起来非常相似。

事实证明，从音频波形（和一般的数字信号）中提取的最佳功能之一自1980年代就已经存在，至今仍是最先进的:梅尔倒频谱系数(Mel Frequency Cepstral Coefficients, mfcc)，由戴维斯和梅尔斯坦在1980年提出。 下面，我们将对MFCC的生成方式以及它们为何在音频分析中有用的技术进行讨论。 这一部分是技术性的，因此在深入探讨之前，让我们定义一些与数字信号处理和音频分析有关的关键术语。 如果您想进一步了解，我们将链接到Wikipedia和其他资源。

混乱而有用的术语

采样频率

在信号处理中， 采样是将连续信号减少为一系列离散值。 采样频率或速率是在一定的固定时间内采集的样本数。 高采样频率导致较少的信息丢失，但计算量较大，低采样频率具有较高的信息丢失量，但计算速度快且成本低。

振幅

声波的幅度是其在一段时间（通常为时间）内变化的量度。 幅度的另一个常见定义是变量的极值之间的差异的大小的函数。

傅里叶变换

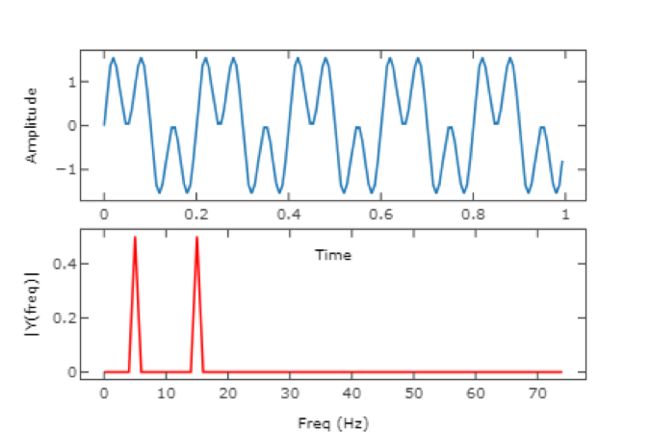
傅立叶变换将时间（信号）的函数分解为组成频率。 以和弦可以通过其构成音符的音量和频率来表达的方式相同，函数的傅立叶变换可以显示基础函数（信号）中每个频率的振幅（量）。

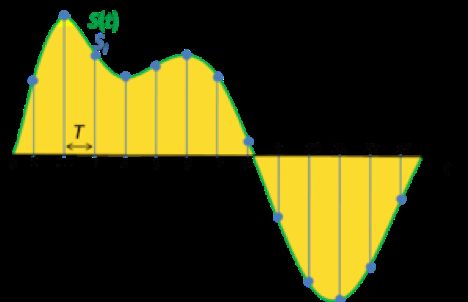
顶部：数字信号； 底部：信号的傅立叶变换

傅立叶变换有多种变体，包括在Librosa库中实现的短时傅立叶变换 ，它涉及将音频信号拆分为帧，然后对每个帧进行傅立叶变换。 通常，在音频处理中，傅立叶是将音频信号分解为其组成频率的一种优雅而有用的方法。

*资源：到目前为止，我在傅立叶变换上发现的最好的视频来自3Blue1Brown *

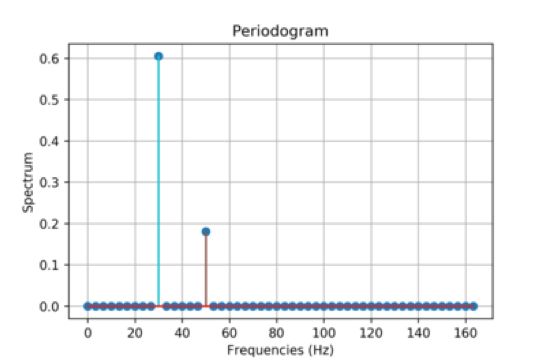
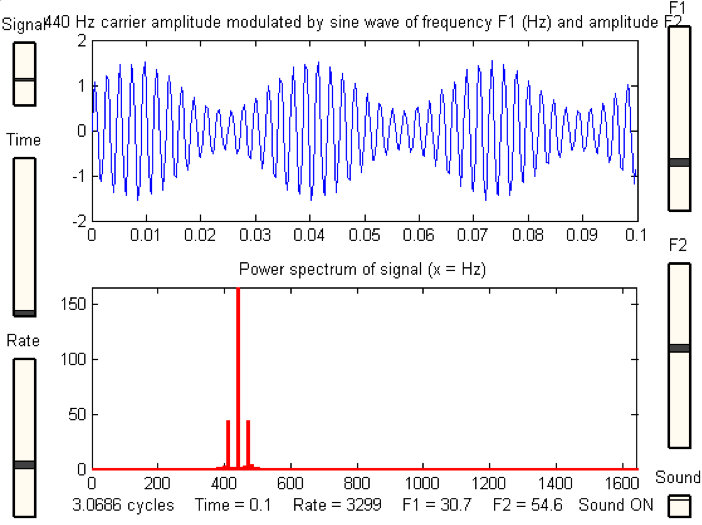
周期图

在信号处理中， 周期图是信号频谱密度的估计值。 上面的周期图显示了〜30Hz和〜50Hz两个正弦基函数的功率谱。 可以将傅立叶变换的输出实质上（不是完全）视为周期图。

光谱密度

时间序列的功率谱是一种描述功率分配到组成该信号的离散频率分量中的方法。 由信号的频率含量测量的统计平均值称为频谱 。 数字信号的频谱密度描述了信号的频率内容。

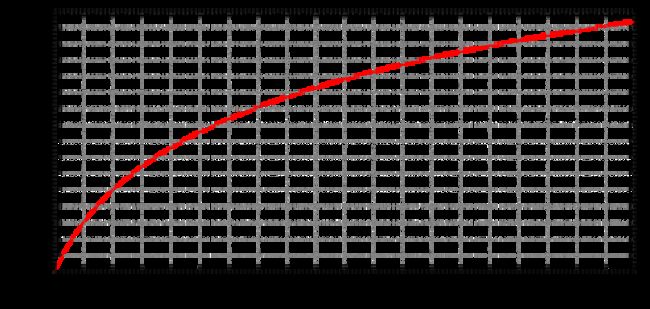
梅尔规模

梅尔音阶是听众判断为彼此之间的距离相等的音调的音阶。 通过将1000 mel的感知音高分配给1000 Hz，可以任意定义mel音阶和正常频率测量之间的参考点。 高于约500 Hz时，听众会判断出越来越大的间隔以产生相等的音高增量。 mel这个名称源于melody一词，表示音阶基于音高比较。

将赫兹转换为m mels的公式为：

倒谱

倒频谱是信号估计功率谱对数的傅立叶变换的结果。

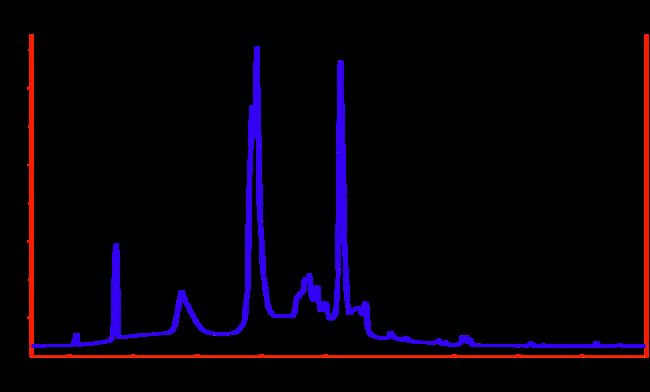
柱状图

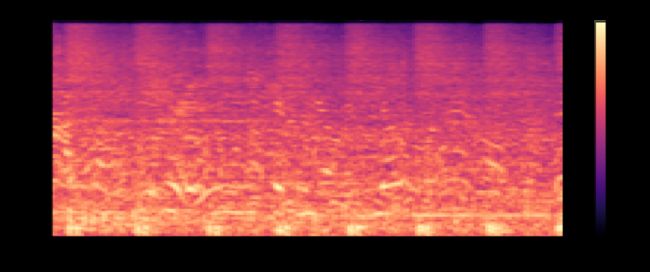
Urbansound8k数据集中音频样本的梅尔频谱图

频谱图是信号频率频谱随时间变化的直观表示。 思考频谱图的一种好方法是将时间间隔数字信号上的周期图堆叠起来。

耳蜗

内耳的螺旋腔包含Corti器官，该器官会响应声音振动而产生神经冲动。

预处理音频：数字信号处理技术

数据集预处理，特征提取和特征工程是我们从基础数据中提取信息的步骤，这些信息在机器学习上下文中对于预测样本类别或某些目标变量的值应有用。 在音频分析中，此过程主要基于查找音频信号的成分，以帮助我们将其与其他信号区分开。

如上所述，MFCC仍然是用于从音频样本中提取信息的先进工具。 尽管像Librosa这样的库为我们提供了一个python线性代码来计算音频样本的MFCC，但基础数学还是有点复杂，因此我们将逐步进行遍历，并包括一些有用的链接以供进一步学习。

为给定音频样本计算MFCC的步骤：

1.将信号切成短帧（时间）
2.计算每帧功率谱的周期图估计
3.将梅尔滤波器组应用于功率谱，并对每个滤波器的能量求和
4.采取对数滤波器组能量的离散余弦变换（DCT）

有关MFCC派生和计算的出色补充读物，请参见此处和此处的博客文章。

1.将信号切成短帧

将音频信号切成短帧很有用，因为它使我们可以将音频采样为离散的时间步长。 我们假设在足够短的时间范围内，音频信号不会改变。 短帧持续时间的典型值在20-40ms之间。 按照惯例，每帧要重叠10-15ms。

*请注意，重叠的框架将使我们最终生成的特征高度相关。 这就是为什么我们必须在所有这些操作结束时进行离散余弦变换的基础。*

2.计算每帧的功率谱

拥有框架后，我们需要计算每个框架的功率谱。 时间序列的功率谱描述了功率在组成该信号的频率分量中的分布。 根据傅立叶分析，任何物理信号都可以分解为多个离散频率或连续范围内的频谱。 根据某信号的频率含量进行分析的统计平均值称为频谱。

资料来源： 马里兰大学，谐波分析和傅立叶变换

我们对每个帧应用短时傅立叶变换以获得每个功率谱。

3.将梅尔滤波器组应用于功率谱，并对每个滤波器的能量求和

一旦有了我们的功率谱，我们仍然要做一些工作。 人类的耳蜗不能很好地分辨附近的频率，并且这种影响只会随着频率的增加而变得更加明显。 梅尔音阶是一种工具，使我们可以比线性频带更接近地估计人类听觉系统的响应。

资料来源： 哥伦比亚

从上面的图表中可以看到，梅尔滤波器随着频率的增加而变宽-我们不太关心较高频率下的变化。 在低频下，人耳可以更清楚地看到差异，因此在我们的分析中，差异更重要，因此滤波器会很窄。

从我们的功率谱，这是由应用傅立叶变换给我们的输入数据中发现的幅度，被分级通过将它们与每个三角形梅尔滤波器相关联。 通常应用这种合并，以使每个系数乘以相应的滤波器增益，因此每个Mel滤波器都会保存一个表示该通道中频谱幅度的加权和。

一旦我们有了滤波器组能量，我们就可以取每个的对数。 这是受到人类听力限制的又一个步骤：人类不会感知音量的线性变化。

要使感知到的声波音量增加一倍，声波的能量必须增加8倍。如果声波已经是高音量（高能量），则该声波能量的大变化听起来可能并没有太大不同。

4.采取对数滤波器组能量的离散余弦变换（DCT）

因为我们的滤波器组能量是重叠的（请参见步骤1），所以它们之间通常存在很强的相关性。 进行离散余弦变换可以帮助解相关能量。

*****

值得庆幸的是， Librosa的创建者已经抽象出了大量的这种数学运算，并且可以轻松地为您的音频数据生成MFCC。 让我们来看一个简单的python示例，以显示此分析的实际效果。

示例项目：Urbansound8k + Librosa

我们将为UrbanSound8k数据集拟合一个简单的神经网络（keras + tensorflow后端）。 首先，让我们加载依赖项，包括numpy、pandas、keras、scikit-learn和librosa。

#### Dependencies ####

#### Import Comet for experiment tracking and visual tools
from comet_ml import Experiment
####

import IPython.display as ipd
import numpy as np
import pandas as pd
import librosa
import matplotlib.pyplot as plt
from scipy.io import wavfile as wav

from sklearn import metrics 
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split 

from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation
from keras.optimizers import Adam
from keras.utils import to_categorical

首先，让我们创建一个Comet实验作为所有工作的包装。 我们将能够自动捕获任何和所有工件（音频文件、可视化效果、模型、数据集、系统信息、培训指标等）。

experiment = Experiment(api_key= "API_KEY" ,
                        project_name= "urbansound8k" )

让我们加载数据集并从数据集中获取每个类的样本。 我们可以使用Comet在视觉和听觉上检查这些样本。

# Load dataset
df = pd.read_csv( 'UrbanSound8K/metadata/UrbanSound8K.csv' )

# Create a list of the class labels
labels  = list(df[ 'class' ].unique())

# Let 's grab a single audio file from each class
files = dict()
for i in range(len(labels)):
    tmp = df[df[' class ']  == labels[i]][: 1 ].reset_index()
    path = 'UrbanSound8K/audio/fold{}/{}' .format(tmp[ 'fold' ][ 0 ], tmp[ 'slice_file_name' ][ 0 ])
    files[labels[i]] = path

我们可以使用librosa的display.waveplot函数查看每个样本的波形。

fig = plt.figure(figsize=( 15 , 15 ))
fig.subplots_adjust(hspace= 0.4 , wspace= 0.4 )
for i, label in enumerate(labels):
    fn = files[label]
    fig.add_subplot( 5 , 2 , i+ 1 )
    plt.title(label)
    data, sample_rate = librosa.load(fn)
    librosa.display.waveplot(data, sr= sample_rate)
plt.savefig( 'class_examples.png' )

我们将此图形保存到我们的Comet实验中。

# Log graphic of waveforms to Comet
experiment.log_image( 'class_examples.png' )

接下来，我们将记录音频文件本身。

# Log audio files to Comet for debugging
for label in labels:
    fn = files[label]
    experiment.log_audio(fn, metadata = { 'name' : label})

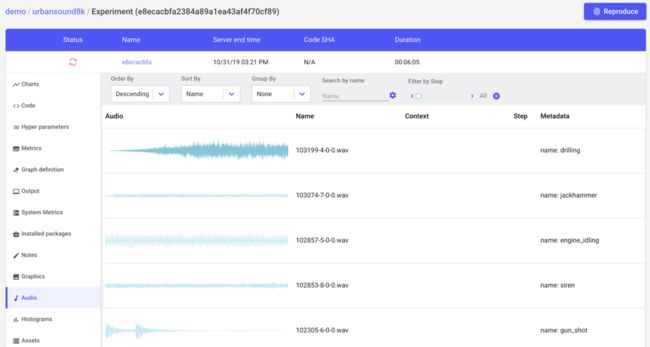
一旦将示例记录到Comet，我们就可以从UI上监听示例、检查元数据等等。

预处理

现在，我们可以从数据中提取特征。 我们将使用librosa，但我们还将显示另一个实用程序scipy.io，以进行比较并观察正在发生的一些隐式预处理。

fn = 'UrbanSound8K/audio/fold1/191431-9-0-66.wav'
librosa_audio, librosa_sample_rate = librosa.load(fn)
scipy_sample_rate, scipy_audio = wav.read(fn)

print( "Original sample rate: {}" .format(scipy_sample_rate))
print( "Librosa sample rate: {}" .format(librosa_sample_rate))

原始采样率：48000
天秤座采样率：22050

Librosa的加载功能将自动将采样率转换为22.05 KHz。 还将标准化介于-1和1之间的位深度。

print( 'Original audio file min~max range: {} to {}' .format(np.min(scipy_audio), np.max(scipy_audio)))
print( 'Librosa audio file min~max range: {0:.2f} to {0:.2f}' .format(np.min(librosa_audio), np.max(librosa_audio)))

>原始音频文件的最小〜最大范围：-1869至1665
> Librosa音频文件的最小〜最大范围：-0.05至-0.05

Librosa还将音频信号从立体声转换为单声道。

plt.figure(figsize=( 12 , 4 ))
plt.plot(scipy_audio)
plt.savefig( 'original_audio.png' )
experiment.log_image( 'original_audio.png' )

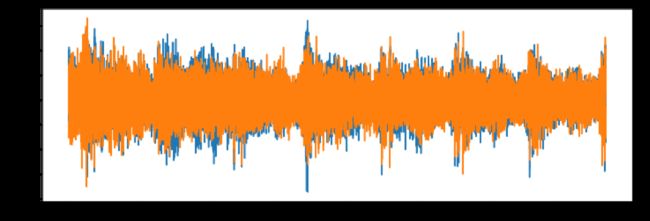
原始音频（请注意，它是立体声的-两个音频源）

# Librosa: mono track
plt.figure(figsize=( 12 , 4 ))
plt.plot(librosa_audio)
plt.savefig( 'librosa_audio.png' )
experiment.log_image( 'librosa_audio.png' )

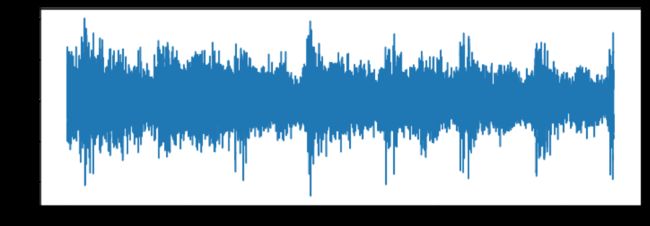
Librosa音频：转换为单声道

使用Librosa从音频中提取MFCC

还记得我们早先了解mel频率倒谱系数的所有数学运算吗？ 使用Librosa，这是从音频中提取它们的方法（使用上面定义的librosa_audio）

mfccs = librosa.feature.mfcc(y=librosa_audio, sr=librosa_sample_rate, n_mfcc = 40 )

就是这样！

print (mfccs.shape)

>（40，173）

Librosa在173帧音频样本上计算了40个MFCC。

plt.figure(figsize=( 8 , 8 ))
librosa.display.specshow(mfccs, sr=librosa_sample_rate, x_axis= 'time' )
plt.savefig( 'MFCCs.png' )
experiment.log_image( 'MFCCs.png' )

我们将定义一个简单的函数为数据集中的每个文件提取MFCC。

def extract_features(file_name):
    audio, sample_rate = librosa.load(file_name, res_type= 'kaiser_fast' ) 
    mfccs = librosa.feature.mfcc(y=audio, sr=sample_rate, n_mfcc= 40 )
    mfccs_processed = np.mean(mfccs.T,axis= 0 )
     
    return mfccs_processed

现在，让我们提取功能。

features = []

# Iterate through each sound file and extract the features 
for index, row in metadata.iterrows():
    
    file_name = os.path.join(os.path.abspath(fulldatasetpath), 'fold' +str(row[ "fold" ])+ '/' ,str(row[ "slice_file_name" ]))
    
    class_label = row[ "class" ]
    data = extract_features(file_name)
    
    features.append([data, class_label])

# Convert into a Panda dataframe 
featuresdf = pd.DataFrame(features, columns=[ 'feature' , 'class_label' ])

现在，我们有了一个数据框，其中每一行都有一个标签（类）和一个要素列，由40个MFCC组成。

featuresdf.head()

featuresdf.iloc[ 0 ][ 'feature' ]

array([ -2 .1579300e +02 , 7.1666122e +01 ,
-1 .3181377e +02 , -5 .2091331e +01 ,
-2 .2115969e +01 , -2 .1764181e +01 ,
-1 .1183747e +01 , 1.8912683e +01 ,
6.7266388e +00 , 1.4556893e +01 ,
-1 .1782045e +01 , 2.3010368e +00 ,
-1 .7251305e +01 , 1.0052421e +01 ,
-6 .0095000e +00 , -1 .3153191e +00 ,
-1 .7693510e +01 , 1.1171228e +00 ,
-4 .3699470e +00 , 7.2629538e +00 ,
-1 .1815971e +01 , -7 .4952612e +00 ,
5.4577131e +00 , -2 .9442446e +00 ,
-5 .8693886e +00 , -9 .8654032e -02 ,
-3 .2121708e +00 , 4.6092505e +00 ,
-5 .8293257e +00 , -5 .3475075e +00 ,
1.3341187e +00 , 7.1307826e +00 ,
-7 .9450034e -02 , 1.7109241e +00 ,
-5 .6942000e +00 , -2 .9041715e +00 ,
3.0366952e +00 , -1 .6827590e +00 ,
-8 .8585770e -01 , 3.5438776e -01 ],
dtype=float32)

现在我们已经成功地从基础音频数据中提取了我们的特征，我们可以构建和训练模型。

模型建立与培训

我们将从将MFCC转换为numpy数组开始，并对分类标签进行编码。

from sklearn.preprocessing import LabelEncoder
from keras.utils import to_categorical

# Convert features and corresponding classification labels into numpy arrays
X = np.array(featuresdf.feature.tolist())
y = np.array(featuresdf.class_label.tolist())

# Encode the classification labels
le = LabelEncoder()
yy = to_categorical(le.fit_transform(y))

我们的数据集将分为训练集和测试集。

# split the dataset 
from sklearn.model_selection import train_test_split 

x_train, x_test, y_train, y_test = train_test_split(X, yy, test_size= 0.2 , random_state = 127 )

让我们定义并编译一个简单的前馈神经网络体系结构。

num_labels = yy.shape[ 1 ]
filter_size = 2

def build_model_graph(input_shape=( 40 ,)):
    model = Sequential()
    model.add(Dense( 256 ))
    model.add(Activation( 'relu' ))
    model.add(Dropout( 0.5 ))
    model.add(Dense( 256 ))
    model.add(Activation( 'relu' ))
    model.add(Dropout( 0.5 ))
    model.add(Dense(num_labels))
    model.add(Activation( 'softmax' ))
    # Compile the model
    model.compile(loss= 'categorical_crossentropy' , metrics=[ 'accuracy' ], optimizer= 'adam' )

    return model

model = build_model_graph()

让我们看一下模型摘要并计算出预训练的准确性。

# Display model architecture summary 
model.summary()

# Calculate pre-training accuracy 
score = model.evaluate(x_test, y_test, verbose= 0 )
accuracy = 100 *score[ 1 ]

print( "Pre-training accuracy: %.4f%%" % accuracy)

训练前准确性：12.2496％

现在是时候训练我们的模型了。

from keras.callbacks import ModelCheckpoint 
from datetime import datetime 

num_epochs = 100
num_batch_size = 32

model.fit(x_train, y_train, batch_size=num_batch_size, epochs=num_epochs, validation_data=(x_test, y_test), verbose= 1 )

培训及时完成：

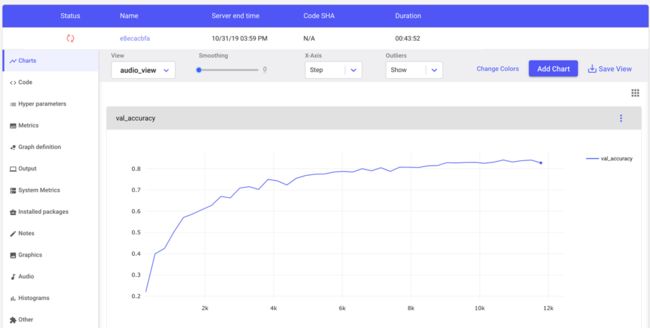
甚至在培训尚未完成之前，Comet都会跟踪有关我们实验的关键信息。 我们可以从Comet UI实时看到我们的准确性和损失曲线（请注意，橙色的旋转轮表示正在进行训练）。

Comet的实验可视化仪表板

训练后，我们可以在火车上评估我们的模型并测试数据。

# Evaluating the model on the training and testing set
score = model.evaluate(x_train, y_train, verbose= 0 )
print( "Training Accuracy: {0:.2%}" .format(score[ 1 ]))

score = model.evaluate(x_test, y_test, verbose= 0 )
print( "Testing Accuracy: {0:.2%}" .format(score[ 1 ]))

训练准确度：93.00％
测试准确度：87.35％

结论

我们的模型训练得很好，但是可能有很多改进的空间，也许使用Comet的Hyperparameter Optimization工具。 在少量的代码中，我们已经能够从音频数据中提取数学上复杂的MFCC，构建和训练神经网络以基于这些MFCC对音频进行分类，并根据测试数据评估我们的模型。

要开始使用Comet， 请单击此处。 Comet是100％免费的公共项目。

原文链接: https://hackernoon.com/how-to-apply-machine-learning-and-deep-learning-methods-to-audio-analyis-wt6p32qz