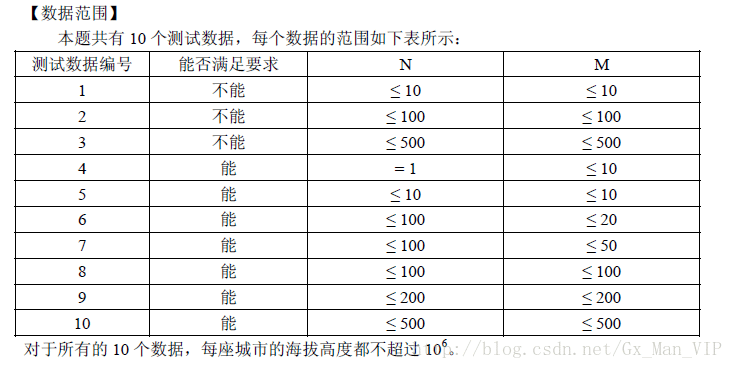
NOIP 提高组 2010 引水入城

题目大意：

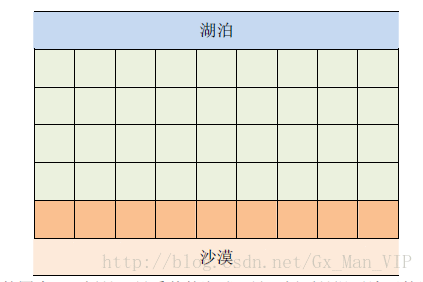
一个N行M列的矩形构成的国家，上边是湖泊，下边是沙漠，如图所示，每个格子都代表一座城市，每座城市都有一个海拔高度。 水往低处流，要求在第一行建蓄水厂，使第N行的沙漠城市能够得到水的供给。如果能，请计算最少建造几个蓄水厂；如果不能，求干旱区中不可能建有水利设施的城市数目。
例：

题解：

BFS+排序+贪心：
首先，推理可得，一个蓄水厂能到第N行的点，这些点必定是连续的，否则此题无解！
因此我们只需要将第一行的每一个点能到第N行的那些点的区间[l,r]存起来即可，l,r用bfs去找
然后对于N个[l,r]的区间，就是找最少的区间数合成[1,M]这个区间
我们将区间排序然后贪心即可
对于bfs而言，有一个重要的优化：
即对于第一行的某个点[1,x]如果它比周边的[1,x-1],[1,x+1]要矮，那么我们可以发现这个区间必定选不上，因为有[1,x-1]或[1,x+1]能经过它，所以它们覆盖的区间[l,r]必定包含[1,x]覆盖的区间[l,r]，所以我们不搜点[1,x]

代码：

const
    dx:array [1..4] of longint=(0,0,1,-1);
    dy:array [1..4] of longint=(1,-1,0,0);

var
    f:array [0..501] of longint;
    a:array [0..501,1..2] of longint;
    c,b:array [0..501,0..501] of longint;
    p,l,r,ans1,ans2,max,pd,i,j,n,m:longint;

function check(aa,bb:longint):boolean;
begin
    if (aa<1) or (aa>n) or (bb<1) or (bb>m) then exit(false);
    if c[aa,bb]=j then exit(false);
    exit(true);
end;

procedure work(x,y:longint);
var
    i:longint;
begin
    if x=n then
    begin
         if ythen l:=y;
         if y>r then r:=y;
    end;
    for i:=1 to 4 do
      if check(x+dx[i],y+dy[i]) then
         if b[x+dx[i],y+dy[i]]then
         begin
              c[x+dx[i],y+dy[i]]:=j;
              work(x+dx[i],y+dy[i]);
         end;
end;

procedure qsort(l,r:longint);
var
    i,j,mid:longint;
begin
    if l>=r then exit;
    mid:=(l+r) div 2;
    i:=l; j:=r;
    repeat
         while (a[i,1]1]) or ((a[i,1]=a[mid,1]) and (a[i,2]2])) do inc(i);
         while (a[j,1]>a[mid,1]) or ((a[j,1]=a[mid,1]) and (a[j,2]>a[mid,2])) do dec(j);
         if i<=j then
         begin
              a[0]:=a[i];a[i]:=a[j];a[j]:=a[0];
              inc(i); dec(j);
         end;
    until i>j;
    qsort(i,r);
    qsort(l,j);
end;

begin
   readln(n,m);
     for i:=1 to n do
       begin
           for j:=1 to m do read(b[i,j]);
           readln;
       end;

     for i:=1 to m do
       begin
            l:=m+1;
            r:=0;
            j:=i;
            work(1,i);
            if r<>0 then
            begin
               inc(p);
               a[p,1]:=l;
               a[p,2]:=r;
            end;
       end;

     qsort(1,p);
     ans1:=1;
     ans2:=0;

     a[0,1]:=0;
     a[0,2]:=0;
     for i:=1 to p do
       if a[i,1]>a[i-1,2]+1
          then ans2:=ans2+(a[i,1]-a[i-1,2]-1);

     if (ans2<>0) or (a[p,2]-a[1,1]+1then
     begin
        writeln(0);
        writeln(ans2);
        halt;
     end;

     ans2:=0;
     i:=1;
     f[0]:=0;
     while i
do
     begin
         if f[f[0]]=m then break;
         j:=a[i,2];
         while (iand (a[i+1,1]<=f[f[0]]+1) do
         begin
               inc(i);
               if a[i,2]>j then j:=a[i,2];
         end;
         inc(f[0]);
         f[f[0]]:=a[i,2];
     end;
     writeln(ans1);
     writeln(f[0]);
end.