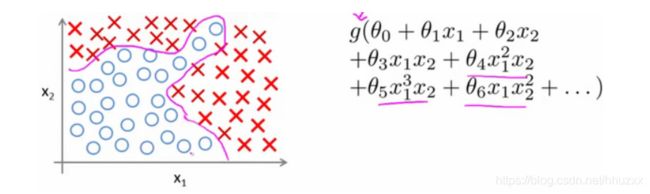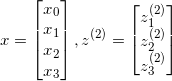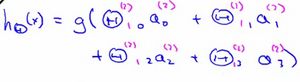吴恩达机器学习 -- 神经网络学习

9.1 非线性假设

无论是线性回归还是逻辑回归都有这样一个缺点，即：当特征太多时，计算的负荷会非常大。

吴恩达老师举了一个例子：

当我们使用 的多次项式进行预测时，我们可以应用的很好。 之前课程学习过，使用非线性的多项式项，能够建立更好的分类模型。假设有非常多的特征，例如大于100个变量，希望用这100个特征来构建一个非线性的多项式模型，结果将是数量非常惊人的特征组合，即便只采用两两特征的组合，也会有接近5000个组合而成的特征。这对于一般的逻辑回归来说需要计算的特征太多了。

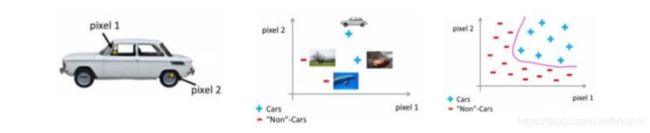
老师紧接着又举了一个计算机视觉的问题：

 假设选用灰度图片，每个像素点只有一个值（RGB有三个），可以选取图片上的两个不同位置上的两个像素，然后训练一个逻辑回归算法利用这两个像素的值来判断图片上是否是汽车。假设采用50x50像素的小图片，并将所有的像素视为特征，会有 2500个特征，如果要进一步将两两特征组合构成一个多项式模型，则会有接近3百万个特征。

普通的逻辑回归模型，不能有效地处理这么多的特征，这时候就需要神经网络模型。

 

9.3 模型展示1

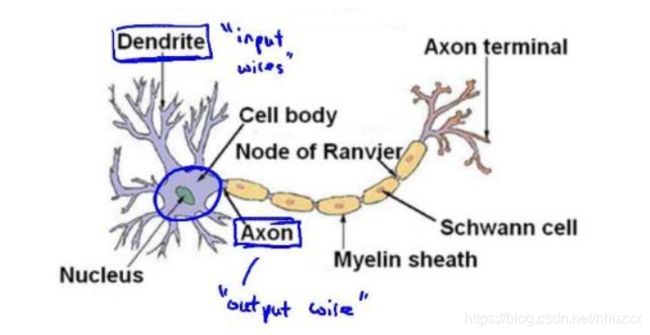
大脑中的神经网络结构如下图所示，Dendrite['dendraɪt]是树突，接收来自其他神经元的信号；Axon['æksɒn]是轴突，向其他神经元输出经过此神经元处理过的信息。

神经网络就是大量神经元相互链接并通过电脉冲来交流的一个网络。

 

神经网络模型建立在很多神经元 之上，每个神经元是一个学习模型。这些神经元（也叫激活单元，activation unit）采纳一些特征作为输入，并且根据本身的模型提供一个输出。

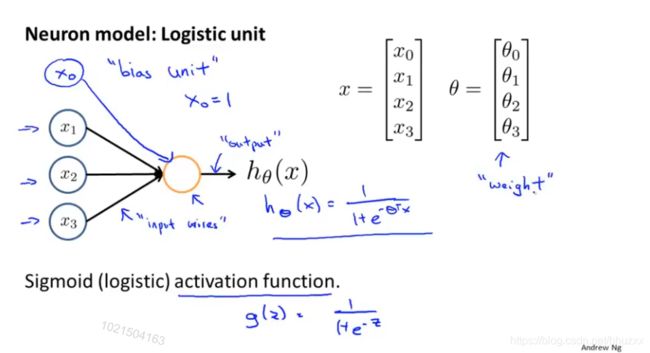
下图是一个以逻辑回归模型作为自身学习模型的神经元示例，在神经网络中，参数 又可被成为权重（weight）。

 类似于神经元的神经网络，效果如下:

其中： 是输入单元，将原始数据输入给它们，处于输入层； 是中间单元，负责将数据进行处理，然后呈递到下一层；最后是输出单元，它负责计算 。

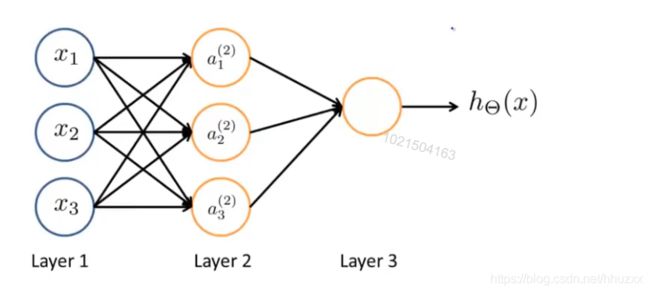
神经网络模型是许多逻辑单元按照不同层级组织起来的网络，每一层的输出变量都是下一层的输入变量。

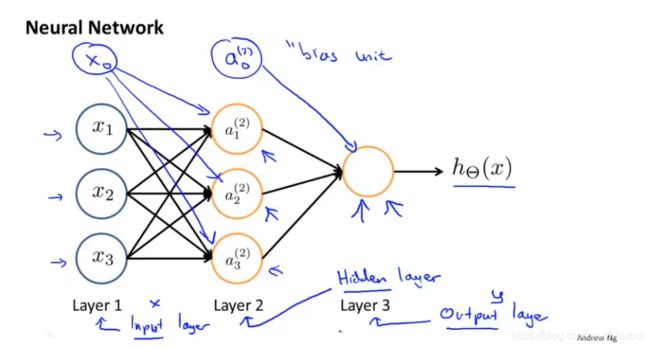
下图为一个3层的神经网络，第一层为输入层（Input Layer），最后一层为输出层（Output Layer），中间一层为隐藏层（Hidden Layers）。我们为每一层都增加一个偏差单位（bias unit）：

一些标记：

：第 层的第 个激活单元

：从第 层映射到第 层的权重矩阵；例如 代表从第1层映射到第2层的权重矩阵，其大小为：第 层的激活单元数量为行数，以第  层的激活单元数加1 为列数的矩阵。

对上述模型，激活单元和输出分别表达为：

把 分别用矩阵表示：

，可得

观察上面的式子，每一个 都是由上一层所有 的和每一个 所对应的 决定的。

把这样从左到右的算法称为前向传播算法( FORWARD PROPAGATION )）

 

9.4 模型展示2

相对于使用循环来编码，利用向量化的方法会使得计算更为简便。以上面的神经网络为例，试着计算第二层的值：

把 定义为 ，其他类似

 

令 ，，计算后添加  。 计算输出的值为：

令 令 ，则

为了更好地了解Neuron Networks的工作原理，先把左半部分遮住：

右半部分其实就是以 ， 按照Logistic Regression的方式输出：

其实神经网络就像是logistic regression，只不过把logistic regression中的输入向量 变成了中间层的 ，可以把 看成更高级的特征值，他们由 决定。

 

9.5 例子与直觉展示①

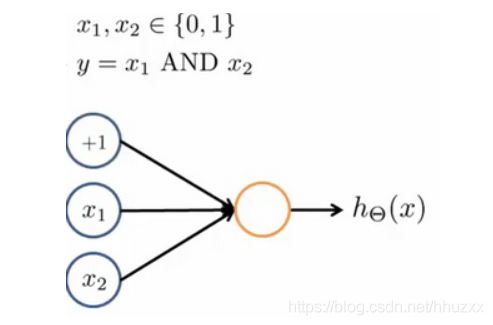
神经网络中，单层神经元（无中间层）的计算可用来表示逻辑运算，比如逻辑与(AND)、逻辑或(OR)。

举例说明：逻辑与(AND)；

 

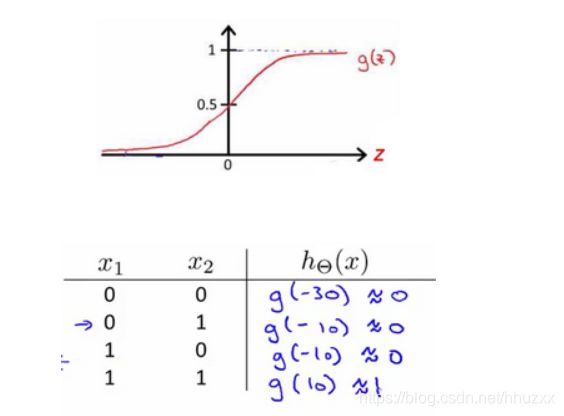
 ，此时

从图中可以看出 AND

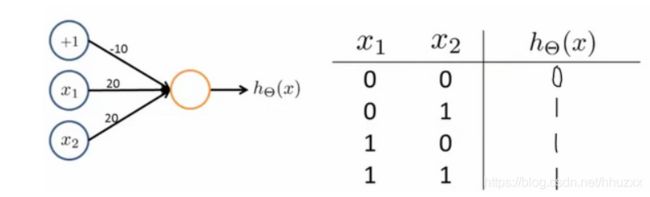
接下来是 OR函数的例子：

 

9.6 例子与直觉展示②

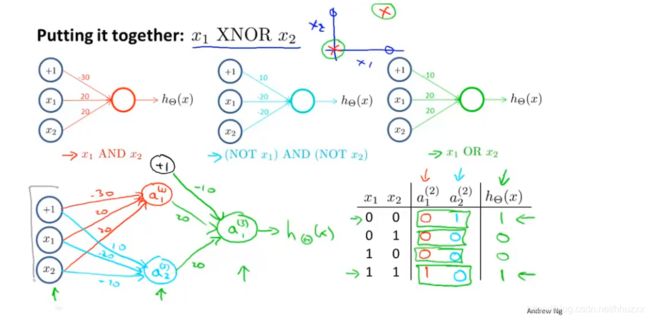
可以利用神经元来组合成更为复杂的神经网络以实现更复杂的运算。例如我们要实现XNOR 功能（输入的两个值必须一样，均为1或均为0），即

这种方法可以逐渐构造出越来越复杂的函数，也能得到更加厉害的特征值。 

 

9.7 多元分类

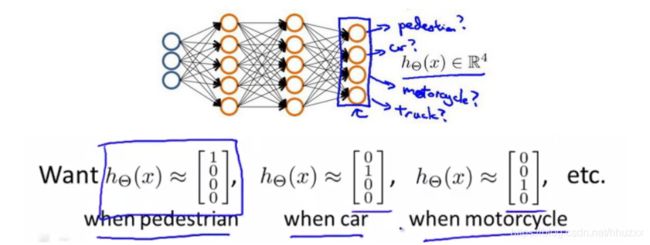
如果要训练一个神经网络算法来识别路人、汽车、摩托车和卡车。

输入 有三个维度，有两个中间层，输出层是一个四维向量，也就是每一个数据在输出层都会出现 ，且a,b,c,d只有一个为1

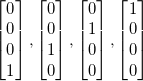
神经网络算法的输出结果为四种可能情形之一：