数据结构：树

树的概念

1.树的定义

树（tree）是n（n>=0）个结点的有限集合。n=0是，称为空树。n>0时满足，该集合满足：

（1.）有且仅有一个称为根（root）的特定结点，该结点没有前驱结点，但有零个或多个直接后继结点；

（2.）除根结点之外的n-1个结点可划分为m(m>=0)个互不相交的有限集T1，T2，,T3，......，Tm，每一个Ti又为一棵树，称为根的子树（Subtree）。每棵子树的根结点有且仅有一个直接前驱，其前驱就是数的根结点，同时可以有零个或多个直接后继结点。

2.树的表示方法

（1.）树形图表示法；

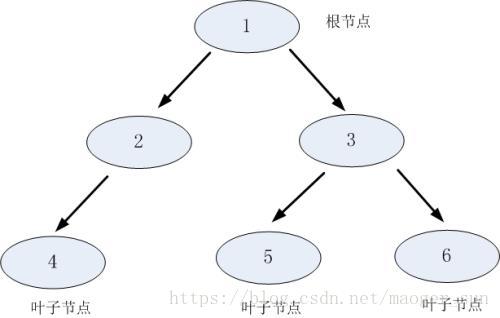
（2.）嵌套集合表示法（文氏图表示法）；

（3.）广义表表示法（嵌套括号表示法）；

（4.）凹入表示法；                      

3.树的基本概念

结点、结点的度、树的度、叶子结点、内部结点、孩子结点、双亲结点、堂兄弟、祖先结点、子孙结点、结点的层次、树的深度、前辈、后辈、森林、有序树、同构；

其中

结点的度：结点拥有子树的个数称为该结点的度；

树的度：树中所有结点的度的最大值；

4.树的抽象数据类型定义

数据对象D、数据关系R、基本操作P：初始化操作、销毁树操作、创建树操作、清空树操作、树判定操作、求树深函数、求树根操作、求双亲函数、求首孩子函数、求右兄弟函数、求结点值函数、结点赋值操作、插入操作、删除操作、遍历操作。

 

二叉树

一、基本概念

1、定义

二叉树是n（n>=0）个结点的有限集合。n=0时，称为空二叉树；当n>0时，该集合由一个根结点及两颗互不相交，被分别称为左子树和右子树的二叉树组成。

特点：①每个结点的度不大于2；②结点每棵子树的位置是明确区分左右的，不能随意改变。

分类：

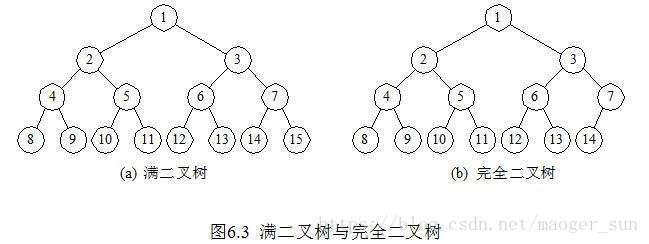
满二叉树：深度为k且含有2^k-1个结点的二叉树；

完全二叉树：深度为k，节点数为n（n<=2^k-1）的二叉树，当且仅当n个结点与满二叉树中连续编号为1至n的结点位置一一对应是，称为完全二叉树。

 

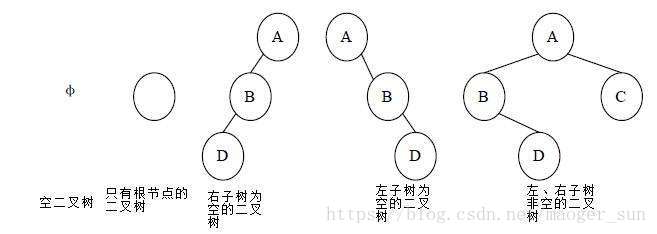
2.二叉树的五种基本形态

 

3.二叉树的抽象数据类型定义

数据对象D，数据关系R，基本操作P，初始化操作，创建二叉树操作，销毁二叉树操作，清空二叉树操作，二叉树判空操作，求二叉树根函数，求二叉树深函数，求双亲函数，求左孩子函数，求右孩子函数，先序遍历操作，中序遍历操作，后序遍历操作，层次遍历操作。

4.二叉树的性质

（1.）在二叉树的第i层上至多有2^（i-1）个结点（i>=1）；

（2.）深度为k的二叉树至多有2^k-1个结点（k>=1);

（3.）对于任意一颗二叉树T，若终结端点树为n0，度为2的节点数为n2，则n0=n1+1；

（4.）具有n个结点的哇怒气按二叉树的深度为⌊log2n⌋+1 ；

ps：数学符号 ⌊⌋ （下有起止，开口向上）表示向下取整，即取比自己小的最大整数。

（5.）对于具有n个结点的完全二叉树，如果按照最满二叉树结点进行连续编号的方式，对所有结点从1开始顺序编号，则对于任意序号为i的结点有：

①如果i=1,则结点i为根，其无双亲结点；如果i>1，则结点i的双亲结点序号为⌊i/2⌋ ；

②如果2i<=n，则结点i的左孩子结点序号为2i，否则，结点无左孩子；

③如果2i+1<=n,则结点i的右孩子结点序号为2i+1，否则，结点i无右孩子。

二、二叉树的存储

（一、）顺序存储结构

对于满二叉树与完全二叉树来说，按照结点连续编号的次序，将各结点数据存放到一组连续的存储单元中，即：用一维数组作存储结构，将二叉树中编好为i的结点存放在数组的第i号分量中。这种方法对于满二叉树和完全二叉树来说十分方便。可是对于一般的二叉树来说，无法体现各结点间的逻辑关系，无法体现结点的双亲及孩子。解决方法：用“空结点”将一般的二二叉树补成一棵“完全二叉树”，但这样会浪费空间。对于任意的二叉树，用链式存储结构最为方便。

顺序存储结构描述

#define MAX 100
typedef sturuct
{
    datatype SeqBiTree[MAX+1];
    int nodemax;
}BiTree;

(二、)链式存储结构

1、结点结构:LChild(指向左孩子)、Data（该结点数据）、RChild（该结点的右孩子）

typedef struct Node
{
    datatype data;
    Struct Node *LChild;
    Struct Node *RChild;
}BiTNode,* BiTree;