LeetCode分类刷题(三)：排序(Sort)

排序算法作为算法和数据结构的重要部分，系统地学习一下是很有必要的。排序是计算机内经常进行的一种操作，其目的是将一组“无序”的记录序列调整为“有序”的记录序列。

排序分为内部排序和外部排序：

• 若整个排序过程不需要访问外存便能完成，则称此类排序问题为内部排序；
• 反之，若参加排序的记录数量很大，整个序列的排序过程不可能在内存中完成，则称此类排序问题为外部排序。

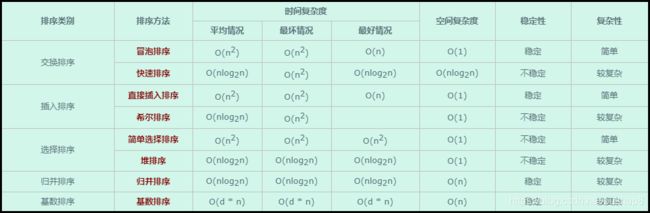
常说的的八大排序算法均属于内部排序。如果按照策略来分类，大致可分为：交换排序、插入排序、选择排序、归并排序和基数排序。如下图所示：

排序分类

下表给出各种排序的基本性能，本篇文章不做详细介绍，具体分析请参看其他博客的详解：

八大排序基本性能对比

下面介绍面试中经常出现的三种排序算法：

• 快速排序：堆排序是一种交换排序：通过一趟排序将要排序的数据分割成独立的两部分，分割点左边都是比它小的数，右边都是比它大的数。然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
• 堆排序：堆排序是一种选择排序，每趟从待排序的记录中选出关键字最小的记录，顺序放在已排序的记录序列末尾，直到全部排序结束为止。堆是一棵顺序存储的完全二叉树：其中每个结点的关键字都不大于其孩子结点的关键字，这样的堆称为小根堆，其中每个结点的关键字都不小于其孩子结点的关键字，这样的堆称为大根堆。
• 归并排序：该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。归并（Merge）排序法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

LeetCode中关于排序的题目有以下三种类型题：

(一)排序之三大排序代码实现：

(二)排序之变形排序相关题目:

(三)排序之归位排序相关题目:

---

(一)排序之三大排序代码实现：

• 快速排序基本思想：通过一趟排序将要排序的数据分割成独立的两部分，分割点左边都是比它小的数，右边都是比它大的数。然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
• 快速排序代码实现：

class Solution {
public:
    int Partition1(vector& nums, int low, int high){
        int key = nums[low];
        while(low < high){
            while(low < high && nums[high] >= key) high--;
            swap(nums[low], nums[high]);
            while(low < high  && nums[low] <= key) low++;
            swap(nums[low], nums[high]);
        }
        return low;
    }
    int Partition2(vector& nums, int low, int high){
        int pos = low;
        for(int i = low; i < high; i++){
            if(nums[i] <= nums[high]) swap(nums[pos++], nums[i]);
        }
        swap(nums[pos++], nums[high]);
        return pos - 1;
    }
    int QuickSort(vector& nums, int low, int high){
        if(low < high){
            int index = Partition2(nums, low, high);
            QuickSort(nums, low, index - 1);
            QuickSort(nums, index + 1, high);
        }
    }
    void sortIntegers(vector& nums) {
        QuickSort(nums, 0, (int)nums.size() - 1);
    }
};

• 堆排序基本思想：堆排序是一种选择排序，每趟从待排序的记录中选出关键字最小的记录，顺序放在已排序的记录序列末尾，直到全部排序结束为止。
• 堆排序代码实现：

class Solution {
public:
    void MaxHeap(vector& nums, int parent, int len){
        int child = 2 * parent + 1;
        while(child < len){
            while(child + 1 < len && nums[child] < nums[child + 1]) child++;
            if(nums[child] > nums[parent]){
                swap(nums[child], nums[parent]);
                parent = child;
                child = 2 * parent + 1;
            }else break;
        }
    }
    void HeapSort(vector& nums){
        int len = nums.size();
        for(int i = (len - 1)/2; i >= 0; i--)
            MaxHeap(nums, i, len);
        for(int j = len ; j > 0; j--){
            MaxHeap(nums, 0, j);
            swap(nums[0], nums[j - 1]);
        }
    }
    void sortIntegers(vector& nums) {
        HeapSort(nums);
    }
};

• 归并排序基本思想：将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
• 归并排序代码实现：

class Solution {
public:
    void MergeArray(vector& nums, int low, int high){
        vector temp(high - low + 1, 0);
        int mid = (low + high)/2, k = 0;
        int i = low, m = mid, j = mid + 1, n = high;
        while(i <= m && j <= n){
            if(nums[i] <= nums[j]) temp[k++] = nums[i++];
            else temp[k++] = nums[j++];
        }
        while(i <= m) temp[k++] = nums[i++];
        while(j <= n) temp[k++] = nums[j++];
        for(int p = 0; p < temp.size(); p++)
            nums[low + p] = temp[p];
    }
    void MergeSort(vector& nums, int low, int high){
        if(low < high){
            int mid = (low + high)/2;
            MergeSort(nums, low, mid);
            MergeSort(nums, mid + 1, high);
            MergeArray(nums, low, high);
        }
    }
    void sortIntegers(vector& nums) {
        MergeSort(nums, 0, (int)nums.size() -1);
    }
};

(二)排序之变形排序相关题目:

75. Sort Colors

• Given an array with n objects colored red, white or blue, sort them in-place so that objects of the same color are adjacent, with the colors in the order red, white and blue. Here, we will use the integers 0, 1, and 2 to represent the color red, white, and blue respectively.
• 题目要求：数组内有n个0,1,2，进行排序，使其按照0,1,2的顺序，即，红，白，蓝的顺序。
• 题目解析：将数组分为三部分，前部（全是0）、中部（全是1）、后部（全是2）三个部分，这样数组中的每个元素就必属于其中之一，那将前部、后部排列好了，中间就自然排列好了。定义两个指针：left、right，left开始指向第一个元素，right指向最后一个元素，然后用指针i遍历数组，根据总的思路，中部我们不动。
• 题目解答：

class Solution {
public:
    void sortColors(vector& nums) {
        int n = nums.size(), left = 0, right = n - 1, i = 0;
        while(i <= right){
            if(nums[i] == 0) swap(nums[i++], nums[left++]);
            else if(nums[i] == 1) i++;
            else swap(nums[i], nums[right--]);
        }
    }
};

324. Wiggle Sort II

• Given an unsorted array nums, reorder it such that nums[0] < nums[1] > nums[2] < nums[3]....
• 题目要求：这道题给了我们一个无序数组，让我们排序成摆动数组，满足nums[0] < nums[1] > nums[2] < nums[3]...
• 题目解析：先给数组排序，然后在做调整。调整的方法是找到数组的中间的数，相当于把有序数组从中间分成两部分，然后从前半段的末尾取一个，在从后半的末尾去一个，这样保证了第一个数小于第二个数，然后从前半段取倒数第二个，从后半段取倒数第二个，这保证了第二个数大于第三个数，且第三个数小于第四个数，以此类推直至都取完。
• 题目解答：

class Solution {
public:
    void wiggleSort(vector& nums) {
        int n = nums.size(),j = (n + 1)/2, k = n;
        sort(nums.begin(), nums.end());
        vector temp = nums;
        for(int i = 0; i < n; i++){
            nums[i] = (i&1) ? temp[--k] : temp[--j];
        }
    }
};

179. Largest Number

• Given a list of non negative integers, arrange them such that they form the largest number.
• 题目要求：这道题给了我们一个数组，让我们将其拼接成最大的数。
• 题目解析：根据题目中给的例子来看，主要就是要给给定数组进行排序，但是排序方法不是普通的升序或者降序，因为9要排在最前面，而9既不是数组中最大的也不是最小的，所以我们要自定义排序方法。对于两个数字a和b来说，如果将其都转为字符串，如果ab > ba，则a排在前面，比如9和34，由于934>349，所以9排在前面，再比如说30和3，由于303<330，所以3排在30的前面。按照这种规则对原数组进行排序后，将每个数字转化为字符串再连接起来就是最终结果。
• 题目解答：

class Solution {
public:
    string largestNumber(vector& nums) {
        string res = "";
        sort(nums.begin(), nums.end(), [](int a, int b){
            return to_string(a) + to_string(b) > to_string(b) + to_string(a);
        });
        for(auto num : nums){
            res += to_string(num); 
        }
        return res[0] == '0' ? "0" : res;
    }
};

451. Sort Characters By Frequency

• Given a string, sort it in decreasing order based on the frequency of characters.
• 题目要求：这道题让我们给一个字符串按照字符出现的频率来排序。
• 题目解析：可以使用STL自带的sort来做，关键就在于重写comparator，由于需要使用外部变量，记得中括号中放入＆，然后我们将频率大的返回，注意一定还要处理频率相等的情况，要不然两个频率相等的字符可能穿插着出现在结果res中，这样是不对的。
• 题目解答：

class Solution {
public:
    string frequencySort(string s) {
        unordered_map hash;
        for(auto ch : s) hash[ch]++;
        sort(s.begin(), s.end(), [&](char& a, char& b){
            return hash[a] > hash[b] || (hash[a] == hash[b] && a < b);
        });
        return s;
    }
};

215. Kth Largest Element in an Array

• Find the kth largest element in an unsorted array. Note that it is the kth largest element in the sorted order, not the kth distinct element.
• 题目要求：这道题让我们求数组中第k大的数字。
• 题目解析：这道题最好的解法应该是下面这种做法，用到了快速排序Quick Sort的思想，这里排序的方向是从小往大排。核心思想是每次都要先找一个中枢点Pivot(key)，然后遍历其他所有的数字，像这道题从小往大排的话，就把小于中枢点的数字放到左半边，把大于中枢点的放在右半边，这样中枢点是整个数组中第几大的数字就确定了，虽然左右两部分不一定是完全有序的，但是并不影响本题要求的结果，所以我们求出中枢点的位置，如果正好是k-1，那么直接返回该位置上的数字；如果大于k-1，说明要求的数字在左半部分，更新右边界，再求新的中枢点位置；反之则更新右半部分，求中枢点的位置；不得不说，这个思路真巧妙啊～
• 题目解答：

class Solution {
public:
    int findKthLargest(vector& nums, int k) {
        int low = 0, n = nums.size(), high = n -1;
        while(low <= high){
            int pos = partition(nums, low, high);
            if(pos < n - k) low = pos + 1;
            else if(pos > n - k) high = pos - 1;
            else return nums[pos];
        }
        return low;
    }
    int partition(vector& nums, int low, int high){
        int key = nums[low];
        while(low < high){
            while(low < high && nums[high] >= key) high--;
            swap(nums[low], nums[high]);
            while(low < high && nums[low] <= key) low++;
            swap(nums[low], nums[high]);
        }
        return low;
    }
};

(三)排序之归位排序相关题目:

442. Find All Duplicates in an Array

• Given an array of integers, 1 ≤ a[i] ≤ n (n = size of array), some elements appear twice and others appear once. Find all the elements that appear twice in this array. Could you do it without extra space and in O(n) runtime?
• 题目要求：给定一个范围在  1 ≤ a[i] ≤ n ( n = 数组大小 ) 的 整型数组，数组中的元素一些出现了两次，另一些只出现一次。找到所有在 [1, n] 范围之间在数组中出现2次的数字。您能在不使用额外空间且时间复杂度为O(n)的情况下完成这个任务吗? 你可以假定返回的数组不算在额外空间内。
• 题目解析：将nums[i]置换到其对应的位置nums[nums[i]-1]上去，比如对于没有缺失项的正确的顺序应该是[1, 2, 3, 4, 5, 6, 7, 8]，而我们现在却是[4,3,2,7,8,2,3,1]，我们需要把数字移动到正确的位置上去，比如第一个4就应该和7先交换个位置，以此类推，最后得到的顺序应该是[1, 2, 3, 4, 3, 2, 7, 8]，我们最后在对应位置检验，如果nums[i]和i+1不等，那么我们将nums[i]存入结果res中即可。
• 题目解答：

class Solution {
public:
    vector findDuplicates(vector& nums) {
        vector res;
        for(int i = 0; i < nums.size(); i++){
            if(nums[i] != nums[nums[i] - 1]){
                swap(nums[i], nums[nums[i] - 1]);
                --i;
            }
        }
        for(int i = 0; i < nums.size(); i++){
            if(nums[i] != i + 1){
                res.push_back(nums[i]);
            }  
        }
        return res;
    }
};

448. Find All Numbers Disappeared in an Array

• Given an array of integers where 1 ≤ a[i] ≤ n (n = size of array), some elements appear twice and others appear once. Find all the elements of [1, n] inclusive that do not appear in this array. Could you do it without extra space and in O(n) runtime? You may assume the returned list does not count as extra space.
• 题目要求：给定一个范围在  1 ≤ a[i] ≤ n ( n = 数组大小 ) 的 整型数组，数组中的元素一些出现了两次，另一些只出现一次。找到所有在 [1, n] 范围之间没有出现在数组中的数字。您能在不使用额外空间且时间复杂度为O(n)的情况下完成这个任务吗? 你可以假定返回的数组不算在额外空间内。
• 题目解析：将nums[i]置换到其对应的位置nums[nums[i]-1]上去，比如对于没有缺失项的正确的顺序应该是[1, 2, 3, 4, 5, 6, 7, 8]，而我们现在却是[4,3,2,7,8,2,3,1]，我们需要把数字移动到正确的位置上去，比如第一个4就应该和7先交换个位置，以此类推，最后得到的顺序应该是[1, 2, 3, 4, 3, 2, 7, 8]，我们最后在对应位置检验，如果nums[i]和i+1不等，那么我们将i+1存入结果res中即可。
• 题目解答：

class Solution {
public:
    vector findDisappearedNumbers(vector& nums) {
        vector res;
        for(int i = 0; i < nums.size(); i++){
            if(nums[i] != nums[nums[i] - 1]){
                swap(nums[i], nums[nums[i] - 1]);
                --i;
            }
        }
        for(int i = 0; i < nums.size(); i++){
            if(nums[i] != i + 1){
                res.push_back(i + 1);
            }  
        }
        return res;
    }
};

41. First Missing Positive

• Given an unsorted integer array, find the smallest missing positive integer.
• 题目要求：这道题让我们找缺失的首个正数。
• 题目解析：我们的思路是把1放在数组第一个位置nums[0]，2放在第二个位置nums[1]，即需要把nums[i]放在nums[nums[i] - 1]上，那么我们遍历整个数组，如果nums[i] != i + 1, 而nums[i]为整数且不大于n，另外nums[i]不等于nums[nums[i] - 1]的话，我们将两者位置调换，如果不满足上述条件直接跳过，最后我们再遍历一遍数组，如果对应位置上的数不正确则返回正确的数
• 题目解答：

class Solution {
public:
    int firstMissingPositive(vector& nums) {
        int n = nums.size();
        for(int i = 0; i < nums.size(); i++){
            if(nums[i] != i + 1){
                if(nums[i] >= 1 && nums[i] <= nums.size() && nums[i] != nums[nums[i]-1]){
                    swap(nums[i], nums[nums[i]-1]);
                    i--;
                }
            }
        }
        for(int i = 0; i < nums.size(); i++){
            if(nums[i] != i + 1)
                return i + 1;
        }
        return n + 1;
    }
};

如果各位看官们，大神们发现了任何错误，或是代码无法通过OJ，或是有更好的解法，或是有任何疑问，意见和建议的话，请一定要在帖子下面评论区留言告知博主啊，多谢多谢，祝大家刷得愉快，刷得精彩，刷出美好未来～