Python小白 Leetcode刷题历程 No.1-No.5 两数之和、两数相加、无重复字符的最长子串、寻找两个有序数组的中位数、最长回文子串
写在前面:
作为一个计算机院的大学生,总觉得仅仅在学校粗略的学习计算机专业课是不够的,尤其是假期大量的空档期,作为一个小白,实习也莫得路子,又不想白白耗费时间。于是选择了Leetcode这个平台来刷题库。编程我只学过基础的C语言,现在在自学Python,所以用Python3.8刷题库。现在我Python掌握的还不是很熟练,算法什么的也还没学,就先不考虑算法上的优化了,单纯以解题为目的,复杂程度什么的以后有时间再优化。计划顺序五个题写一篇日志,希望其他初学编程的人起到一些帮助,写算是对自己学习历程的一个见证了吧。
有一起刷LeetCode的可以关注我一下,我会一直发LeetCode题库Python3解法的,也可以一起探讨。
觉得有用的话可以点赞关注下哦,谢谢大家!
········································································································································································
题解框架:
1.题目,难度
2.题干,题目描述
3.题解代码(Python3(不是Python,是Python3))
4.或许有用的知识点(不一定有)
5.解题思路
6.优解代码及分析(当我发现有比我写的好很多的代码和思路我就会写在这里)
········································································································································································
No.1.两数之和
难度:简单
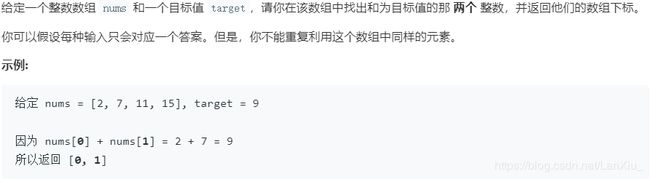
题目描述:
题解代码(Python3.8)
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
for i in range(len(nums)-1):
for j in range(i+1,len(nums)):
if nums[i] + nums[j] == target:
return [i,j]
解题思路:
暴力方法,运用两个for循环遍历数组完成表达式s[i] + s[j]的遍历,因为加法不用区分s[i]和s[j]的顺序,因此i属于range(len(nums)-1),j属于range(i+1,len(nums)),判断是否有s[i] + s[j] = sum即可,因为只需要返回[i,j],所以只需要在两个for循环内return [i,j]即可跳出两层for循环。
No.2.两数相加
难度:中等
题目描述:
题解代码(Python3.8)
class Solution:
def addTwoNumbers(self, l1: ListNode, l2: ListNode) -> ListNode:
def add(a,b,c):
if not( a or b ):
return ListNode(1) if c else None
a = a if a else ListNode(0)
b = b if b else ListNode(0)
val = a.val + b.val + c
c= val/10 if val>=10 else 0
a.val = val%10
a.next = add(a.next,b.next,int(c))
return a
return add(l1,l2,0)
或许有用的知识点:
ListNode的一些介绍:
变量值=List Node.val
指针指向下一节点=List Node.next
解题思路:
这个其实可以类比加法器,两个List Node中每一位相加,得到一个结果和一个进位,结果存在L1中该位上,进位加在L1..next上。我们可以把这一过程定义为函数add,然后对add进行递归即可。
No.3.无重复字符的最长子串
难度:中等
题目描述:
题解代码(Python3.8)
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
if not s:
return 0
left = 0
lookup = set() #定义为set形式去重
max_len = 0
cur_len = 0
for i in range(len(s)):
cur_len += 1
while s[i] in lookup:
lookup.remove(s[left])
left += 1
cur_len -= 1
if cur_len > max_len:
max_len = cur_len
lookup.add(s[i])
return max_len
或许有用的知识点:
set(list)函数可以将list中重复元素过滤,set是无序的,set.add(key)可以在set中添加元素,set.remove(key)可以在set中删除元素。
滑动窗口:其实就是一个队列,比如例题中的 abcabcbb,进入这个队列(窗口)为 abc 满足题目要求,当再进入 a,队列变成了 abca,这时候不满足要求。所以,我们要移动这个队列!我们只要把队列的左边的元素移出就行了,直到满足题目要求!一直维持这样的队列,找出队列出现最长的长度时候,求出解!
解题思路:
暴力方法,先单列出len(s)=0和len(s)=1的情况,再对其他情况进行循环求解。设置一个起始位置下标j=0,一重for循环遍历i in range(1,len(s)),第二重for循环遍历m in range(j,i)。再把k置零,第二重循环中,每次s[m] != s[i] 则k++,若k == i-j 则说明s[j]到s[i]无重复字符,将将其长度与max1比较即可。若出现s[m] == s[i]则令j=m+1,k置零。
NO.4.寻找两个有序数组的中位数
难度:困难
题目描述:
题解代码(Python3.8)
class Solution:
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
n=len(nums1)+len(nums2)
nums1=nums1+nums2
nums1.sort()
if n%2 != 0:
num = nums1[(n-1)//2]
else:
num = (nums1[n//2]+nums1[(n//2)-1])/2
return num
或许有用的知识点:
看到了复杂度为O(log(m+n))和有序数列,不难想到使用「二分查找」来解决。
这是408考试的原题,含金量还是比较高的。
解题思路:
按题目要求,复杂度应为 O(log(m + n)),应采用二分算法,当时我还没学过,就直接冒泡排序了。
这道题应该是难在算法上,我没考虑算法,冒泡排序完按奇偶项取中位数即可。
优解代码及分析:
优解代码(Python3.8)
class Solution:
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
m, n = len(nums1), len(nums2)
# 这里为了保证nums1一定是长度较小的数组
if m > n:
nums1, nums2, m, n = nums2, nums1, n, m
# 题目给定数组不会同时为空,也就是m^2+n^2≠0,由于m≤n,故只要n≠0即可
if not n:
raise ValueError("数组长度不同时为零")
i_min, i_max = 0, m
# left集合元素数量,如果m+n是奇数,left比right多一个数据
count_of_left = (m + n + 1) // 2
while i_min <= i_max:
i = (i_min + i_max) // 2 # left有i个nums1的元素
j = count_of_left - i # left有j个nums2的元素
if i > 0 and nums1[i - 1] > nums2[j]:
i_max = i - 1 # i太大,要减少
elif i < m and nums1[i] < nums2[j - 1]:
i_min = i + 1 # i太小,要增加
else:
if i == 0:
max_of_left = nums2[j - 1]
elif j == 0:
max_of_left = nums1[i - 1]
else:
max_of_left = max(nums1[i - 1], nums2[j - 1])
if (m + n) % 2:
return float(max_of_left) # 结果是浮点数
if i == m:
min_of_right = nums2[j]
elif j == n:
min_of_right = nums1[i]
else:
min_of_right = min(nums1[i], nums2[j])
return (max_of_left + min_of_right) / 2.0 # 结果为浮点数
分析:
No.5.最长回文子串
难度:中等
题目描述:
题解代码(Python3.8)
class Solution:
def longestPalindrome(self, s: str) -> str:
l=len(s)
if l==0:
sm=""
if l==1 or s[::]==s[::-1]:
sm=s
else:
dm=1
sm=s[0]
l=len(s)
for i in range(l-1):
for j in range(i+1,l):
d=j-i+1
if d>dm:
if (i+j)%2 == 0:
if s[i: (i+j)//2 ] == s[j: (i+j)//2 :-1]:
sm=s[i:j+1]
dm=d
else:
if s[i: ((i+j)//2)+1 ] == s[j: (i+j)//2 :-1]:
sm=s[i:j+1]
dm=d
return sm
或许有用的知识点:
切片操作:通常一个切片操作要提供三个参数 [start_index: stop_index: step] :
start_index是切片的起始位置
stop_index是切片的结束位置(不包括)
step可以不提供,默认值是1,步长值不能为0,不然会报错ValueError。
这道题会用到动态规划的知识。
dp = [[False for _ in range(size)] for _ in range(size)]可以理解为Python创建二维数组的一种写法。
解题思路
对于没有算法基础的我来说,Python的切片功能极其好用,他为我减少了一阶的复杂度。我们先用两个for循环遍历所有的s[i]到s[j]区间,对其正向切片和反向切片,若值相同,即为一个回文子串,与最长回文子串比较长度即可。
优解代码及分析:
优解代码(Python3.8)
class Solution:
def longestPalindrome(self, s: str) -> str:
size = len(s)
if size < 2:
return s
dp = [[False for _ in range(size)] for _ in range(size)]
max_len = 1
start = 0
for i in range(size):
dp[i][i] = True
for j in range(1, size):
for i in range(0, j):
if s[i] == s[j]:
if j - i < 3:
dp[i][j] = True
else:
dp[i][j] = dp[i + 1][j - 1]
else:
dp[i][j] = False
if dp[i][j]:
cur_len = j - i + 1
if cur_len > max_len:
max_len = cur_len
start = i
return s[start:start + max_len]
分析:
1、思考状态
状态先尝试“题目问什么,就把什么设置为状态”。然后考虑“状态如何转移”,如果“状态转移方程”不容易得到,尝试修改定义,目的仍然是为了方便得到“状态转移方程”。
2、思考状态转移方程(核心、难点)
状态转移方程是非常重要的,是动态规划的核心,也是难点,起到承上启下的作用。
技巧是分类讨论。对状态空间进行分类,思考最优子结构到底是什么。即大问题的最优解如何由小问题的最优解得到。
归纳“状态转移方程”是一个很灵活的事情,得具体问题具体分析,除了掌握经典的动态规划问题以外,还需要多做题。如果是针对面试,请自行把握难度,我个人觉得掌握常见问题的动态规划解法,明白动态规划的本质就是打表格,从一个小规模问题出发,逐步得到大问题的解,并记录过程。动态规划依然是“空间换时间”思想的体现。
3、思考初始化
初始化是非常重要的,一步错,步步错,初始化状态一定要设置对,才可能得到正确的结果。
角度 1:直接从状态的语义出发;
角度 2:如果状态的语义不好思考,就考虑“状态转移方程”的边界需要什么样初始化的条件;
角度 3:从“状态转移方程”方程的下标看是否需要多设置一行、一列表示“哨兵”,这样可以避免一些边界的讨论,使得代码变得比较短。
4、思考输出
有些时候是最后一个状态,有些时候可能会综合所有计算过的状态。
5、思考状态压缩
“状态压缩”会使得代码难于理解,初学的时候可以不一步到位。先把代码写正确,然后再思考状态压缩。
状态压缩在有一种情况下是很有必要的,那就是状态空间非常庞大的时候(处理海量数据),此时空间不够用,就必须状态压缩。
这道题比较烦人的是判断回文子串。因此需要一种能够快速判断原字符串的所有子串是否是回文子串的方法,于是想到了“动态规划”。
“动态规划”最关键的步骤是想清楚“状态如何转移”,事实上,“回文”是天然具有“状态转移”性质的:
一个回文去掉两头以后,剩下的部分依然是回文(这里暂不讨论边界)。
依然从回文串的定义展开讨论:
1、如果一个字符串的头尾两个字符都不相等,那么这个字符串一定不是回文串;
2、如果一个字符串的头尾两个字符相等,才有必要继续判断下去。
(1)如果里面的子串是回文,整体就是回文串;
(2)如果里面的子串不是回文串,整体就不是回文串。
即在头尾字符相等的情况下,里面子串的回文性质据定了整个子串的回文性质,这就是状态转移。因此可以把“状态”定义为原字符串的一个子串是否为回文子串。
第 1 步:定义状态
dp[i][j] 表示子串 s[i, j] 是否为回文子串。
第 2 步:思考状态转移方程
这一步在做分类讨论(根据头尾字符是否相等),根据上面的分析得到:
dp[i][j] = (s[i] == s[j]) and dp[i + 1][j - 1]
分析这个状态转移方程:
(1)“动态规划”事实上是在填一张二维表格,i 和 j 的关系是 i <= j ,因此,只需要填这张表的上半部分;
(2)看到 dp[i + 1][j - 1] 就得考虑边界情况。
边界条件是:表达式 [i + 1, j - 1] 不构成区间,即长度严格小于 2,即 j - 1 - (i + 1) + 1 < 2 ,整理得 j - i < 3。
这个结论很显然:当子串 s[i, j] 的长度等于 2 或者等于 3 的时候,我其实只需要判断一下头尾两个字符是否相等就可以直接下结论了。
如果子串 s[i + 1, j - 1] 只有 1 个字符,即去掉两头,剩下中间部分只有 11 个字符,当然是回文;
如果子串 s[i + 1, j - 1] 为空串,那么子串 s[i, j] 一定是回文子串。
因此,在 s[i] == s[j] 成立和 j - i < 3 的前提下,直接可以下结论,dp[i][j] = true,否则才执行状态转移。
(这一段看晕的朋友,直接看代码吧。我写晕了,车轱辘话来回说。)
第 3 步:考虑初始化
初始化的时候,单个字符一定是回文串,因此把对角线先初始化为 1,即 dp[i][i] = 1 。
事实上,初始化的部分都可以省去。因为只有一个字符的时候一定是回文,dp[i][i] 根本不会被其它状态值所参考。
第 4 步:考虑输出
只要一得到 dp[i][j] = true,就记录子串的长度和起始位置,没有必要截取,因为截取字符串也要消耗性能,记录此时的回文子串的“起始位置”和“回文长度”即可。
第 5 步:考虑状态是否可以压缩
因为在填表的过程中,只参考了左下方的数值。事实上可以压缩,但会增加一些判断语句,增加代码编写和理解的难度,丢失可读性。在这里不做状态压缩。
下面是编码的时候要注意的事项:总是先得到小子串的回文判定,然后大子串才能参考小子串的判断结果。
思路是:
1、在子串右边界 j 逐渐扩大的过程中,枚举左边界可能出现的位置;
2、左边界枚举的时候可以从小到大,也可以从大到小。