leetcode数论专题

367.完全平方数

1 = 1;
4 = 1 + 3;
9 = 1 + 3 + 5;
16 = 1 + 3 + 5 + 7;
N*N = 1 + 3 + 5 + … + (2N - 1)

数学规律

时间：$O(sqrt(num))$
空间：$O(1)$

class Solution 
{
public:
    bool isPerfectSquare(int num) 
    {
        int num1 = 1;
        while(num > 0) 
        {
            num -= num1;
            num1 += 2;
        }
        return num == 0;
    }
};

二分法

时间：$O(logn)$
空间：$O(1)$

//二分法
class Solution {
public:
	bool isPerfectSquare(int num) {
		long low = 1, high = num;
		while (low < high) {
			long  mid = (low + high) / 2;
			if (mid * mid == num)
				return true;
			else if (mid * mid > num)
				high = mid - 1;
			else
				low = mid + 1;
		}
		if (low * low == num)
			return true;
		return false;
	}
};

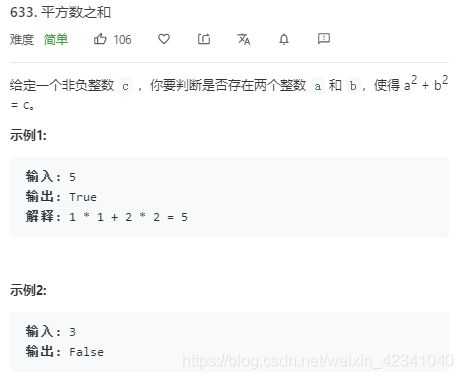
633.平方数之和

双指针

时间：$O(sqrt(c))$
空间：$O(1)$

class Solution {
public:
	bool judgeSquareSum(int c) {
		int sqr = sqrt(c);
		if (sqr * sqr == c)//如果能直接开平方，则另一个数看做0
			return true;
		long low = 1, high = sqr;//long在64位编译器下8字节，最大数2^63-1,unsigned int最大2^32-1
		
		while (low <= high) {
			long n = low * low + high * high;
			if (n == c )
				return true;
			else if (n < c)
				++low;
			else
				--high;
		}
		return false;
	}
};

483.最小好进制

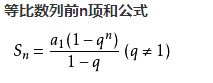
问题等价于求最小的正整数 k，满足存在一个正整数 m, 使得${\sum }_{i=0}^m{k}^i=\frac{1-k^{m+1}}{1-k}=n$, $1+k+k^2+k^3+...+k^m=n.$求最小的k,实际上等价于求最大的m.


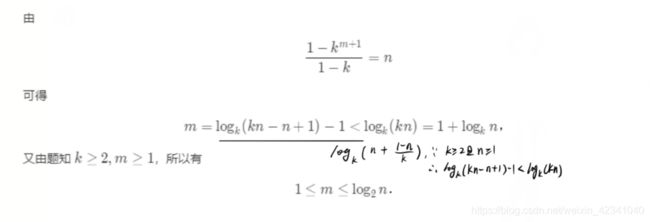
atoi函数：将字符串转化为int类型变量

atol函数：将字符串转化为long类型变量

atoll函数：将字符串转化为long long类型变量

atof函数：将字符串转化为double类型变量

class Solution {
public:
	string smallestGoodBase(string n) {
		long long n_n = atoll(n.c_str());
		for (int m = log2(n_n); m >= 1; --m) {
			unsigned long long low = 2, high = powl(n_n, 1.0 / m) + 1, mid, sum;//pow出错，用powl
			while (low <= high) {
				mid = (low + high) / 2;
                //求1 + mid + mid^2 + mid^3 +...+mid^m 的公式
				sum = 1;
				for (int j = 0; j < m; ++j) {
					sum = sum * mid + 1;
				}
                //sum = (1 - pow(mid, m + 1)) / (1 - mid);//直接用公式：超时
				if (sum == n_n)
					return to_string(mid);
				else if (sum < n_n)
					low = mid + 1;
				else
					high = mid - 1;
			}
          
		}
		return "";
	}
};

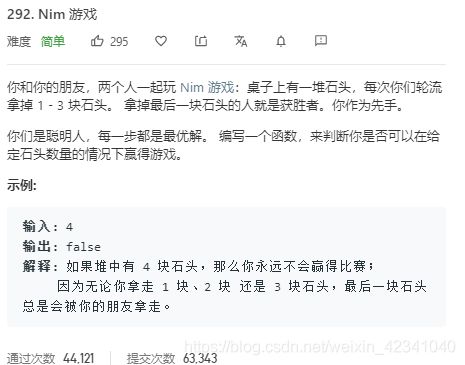
Nim游戏

思路

class Solution {
public:
    bool canWinNim(int n) {
        return n % 4;//被4整除，0==false
    }
};

50.Pow(x, n)

快速幂

非迭代

思路

假设求$a^b$,按照朴素算法就是把a连乘b次，这样一来时间复杂度是O(n)级，快速幂能做到O(logn)
首先把b写成它的二进制形式，设该二进制数第$i$位的权值为$2^{i-1}$
那么假设$b=11$，11的二进制是1011，11 = 2³×1 + 2²×0 + 2¹×1 + 2º×1=2³+2¹+2º，所以：$a^{11}=a^{2^3}\ast a^{2^1}\ast a^{2^0}$

代码中n&1是取末位，只有当前位为1时才要乘； n/=2是将n右移一位，取新的位做末位；x*=x是下一次要乘的因子

class Solution {
public:
	double myPow(double x, int n) {
		int temp_n = n;
		double ans = 1;
		while (n) {
			if (n & 1) {//和1与取末尾
				ans *= x;
			}
			x *= x;
			n /= 2;//数字右移1，每次取新的位做末位
		}
		return temp_n >= 0 ? ans : 1 / ans;

	}
};

复杂度

时间：$O(logn)$
空间：$O(1)$

974.和可被K整除的子数组

思路1：前缀和+动态规划（超时）

class Solution1 {
public:
	int subarraysDivByK(vector<int>& A, int K) {
		//int res = 0;
		int sz = A.size();
		//A数组的前n项总和
		vector<int>sum(sz + 1, 0);
		for (int i = 1; i < sz + 1; i++) {
			sum[i] = sum[i - 1] + A[i - 1];
		}
		vector<int>dp(sz + 1, 0);
		
		for (int i = 1; i < sz + 1; ++i) {
			//取这一项
			if (sum[i] % K == 0)
				dp[i]++;
			for (int j = 1; j < i; ++j) {
				if ((sum[i] - sum[j]) % K == 0)
					dp[i]++;
					
			}
			dp[i] += dp[i - 1];//不取这一项
		}
		return dp[sz];
	}
};

思路二：前缀和+同余定理

class Solution {
public:
	int subarraysDivByK(vector<int>& A, int K) {
		unordered_map<int, int> record = { {0, 1} };//考虑了前缀和本身被 K 整除的情况
		//key：前缀和 value: 该和出现的次数
		int sum = 0, ans = 0;
		for (int elem : A) {
			sum += elem;
			int modulus = (sum % K + K) % K;//处理负数，正数情况下等于 sum % k
			//比如：4和-6
			//(4 - (-6))% 5 = 0
			//4%5=4 (-6)%5=-1,所以要用上式处理((-6)%5+5)%5=4 ==>4和-6同余于5
			if (record.count(modulus)) {
				ans += record[modulus];
			}
			++record[modulus];//出现的次数加1
		}
		return ans;
	}
};

复杂度

15.三数之和

class Solution {
public:
	vector<vector<int>> threeSum(vector<int>& nums) {
		int n = nums.size();
        vector<vector<int>> ans;
        if(n<3)return ans;
		sort(nums.begin(), nums.end());
		
		if (nums[0] > 0 || nums[n - 1] < 0)//优化1
			return ans;
		// 枚举 a
		for (int first = 0; first < n; ++first) {
			if (nums[first] > 0)//优化2
				break;
			// 需要和上一次枚举的数不相同
			if (first > 0 && nums[first] == nums[first - 1]) {
				continue;
			}
			// c 对应的指针初始指向数组的最右端
			int third = n - 1;
			int second = first + 1;
			int target = -nums[first];
			// 枚举 b
			while (second < third) {
				if (nums[third] < 0)//优化3
					break;
				// 需要和上一次枚举的数不相同
				if (second > first + 1 && nums[second] == nums[second - 1]) {
                    second++;
					continue;
				}
				if (nums[second] + nums[third] > target)--third;
				else if (nums[second] + nums[third] < target)++second;
				else {
					ans.push_back({ nums[first], nums[second], nums[third] });
                    --third;
					++second;
				}
			}
	
		}
		return ans;
	}
};

复杂度