数据结构：时间复杂度与空间复杂度

算法的复杂度 ：

首先，算法的时间复杂度与空间复杂度 统称为算法的复杂度。

时间复杂度：

时间复杂度其实就是一个函数，，该函数计算的是执行基本操作的次数。

算法分析的分类：

算法存在最好、平均和最坏情况：
最坏情况：任意输入规模的最大运行次数(上界)
平均情况：任意输入规模的期望运行次数
最好情况：任意输入规模的最小运行次数，通常最好情况不会出现 (下界)
在实际中通常关注的是算法的最坏运行情况，即:任意输入规模N，算法的最长运行时间。理由如下：

一个算法的最坏情况的运行时间是在任意输入下的运行时间上界
对于某些算法，最坏的情况出现的较为频繁
大体上看，平均情况与最坏情况一样差
因此：一般情况下使用O渐进表示法来计算算法的时间复杂度

时间复杂度之大O渐进表示法

一个算法语句总的执行次数是关于问题规模N的某个函数，记为f(N)，N 称为问题的规模。语句总的执行次数记为T(N)，当N不断变化时，T(N)也 在变化，算法执行次数的增长速率和f(N)的增长速率相同。则有T(N) = O(f(N))，称O(f(n))为时间复杂度的O渐进表示法。

空间复杂度：

空间复杂度：函数中创建对象的个数关于问题规模函数表达式，一般情况下用O 的渐进表示法表示

时间复杂度与空间复杂度的计算：

一般的时间复杂度的算法：
1.用常数1取代运行时间中的所有加法常数
2.在修改后的运行次数函数中，只保留最高阶项
3.如果最高阶项系数存在且不是1，则去除与这个项相乘的常数

下面举个例子：

void TEST(int n)
{
    int iCount = 0;
    for (int iIdx = 0; iIdx < 10; ++iIdx)
    {
        iCount++;
    }
}

这里我们可以计算出循环的系数为10次，然后我们根据时间复杂度的计算法则1，就可以将10用1代替，所以上述函数的时间复杂度为O(1)。而空间复杂度我们可以看出在这里只用开辟一块空间就可以够我们上面这个函数的变量创建，而不需要开辟新的空间，所以我们很容易得到它的空间复杂度为O（1）；

void Test1(int n)
{
    int iCount = 0;
    for (int iIdx = 0; iIdx < 10; iIdx++)
    {
        iCount++;
    }
    for (int iIdx = 0; iIdx < 2 * n; ++iIdx)
    {
        iCount++;
    }
    for (int i = 0; i < n; ++i)
    {
        for (int j = 0; j < n; ++j)
        {
            iCount++;
        }
    }
}

上面这段代码我们同样先计算出运算的总次数：10+2n+n^2;根据时间复杂度算法规则我们可以得到它的时间复杂度为O(n^2);而这里它同样只用开辟一块空间就可以放这个函数的变量，而不需要开辟新的空间，所以很容易得到它的空间复杂度为O(1).

二分法查找时间复杂度以及空间复杂度的算法：

先看二分法查找的程序：

int binary_search(int arr[], int key, int sz)  
{  
       int left = 0;  
       int right = sz - 1;  
       int mid = 0;  
       while (left <= right)  
       {  
        mid = left + (right - left) / 2;  
              if (arr[mid] == key)  
              {  
                     return mid;  
              }  
              else if (arr[mid] < key)  
              {  
                     left = mid + 1;  
              }  
              else  
              {  
                     right = mid - 1;  
              }  
       }  
       if (left <= right)  
              return mid;O  
       else  
              return 0;  
}  

二分法查找其实就是将我们要找的数与数组中n个元素中中间的那个元素对比，如果要找的数比中间这个数大（反之我们就在这个数的左边找），我们就在中间的这个数元素右边的数中继续找中间的数与要找的数比较，然后一直循环着个过程一直到找到这个数为止。找到这个数循环过程的总次数就是我们所求的时间复杂度。即：Time=Log₂n。则时间复杂度就为O(Log₂n),在二分查找里因为没有新空间的开辟，只需要开辟固定大小的空间就可以创建这几个变量，所以它的空间复杂度为O(1)。

递归法的时间复杂度与空间复杂度的计算：

递归算法时间复杂度：递归总次数*每次递归次数
递归求n的阶乘：

int fac(int n)
{
    if (n == 1 || n == 0)
    {
        return 1;
    }
    return n * fac(n - 1);

}

在这里我们可以看出这里当n=5时，即我们想要得到5的阶乘时我们就需要首先知道4的阶乘，知道4的阶乘我们就必须知道3的阶乘，知道3的阶乘我们就必须知道2的阶乘，知道我的阶乘我们得知道1的阶乘。因此这一过程中我们调用了五次这个函数，所以时间复杂度为：O（n)。这一循环的过程我们可以用下面这张图来看。

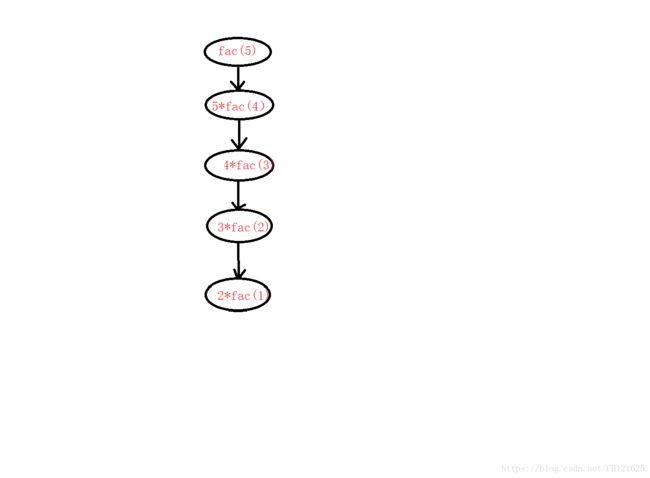
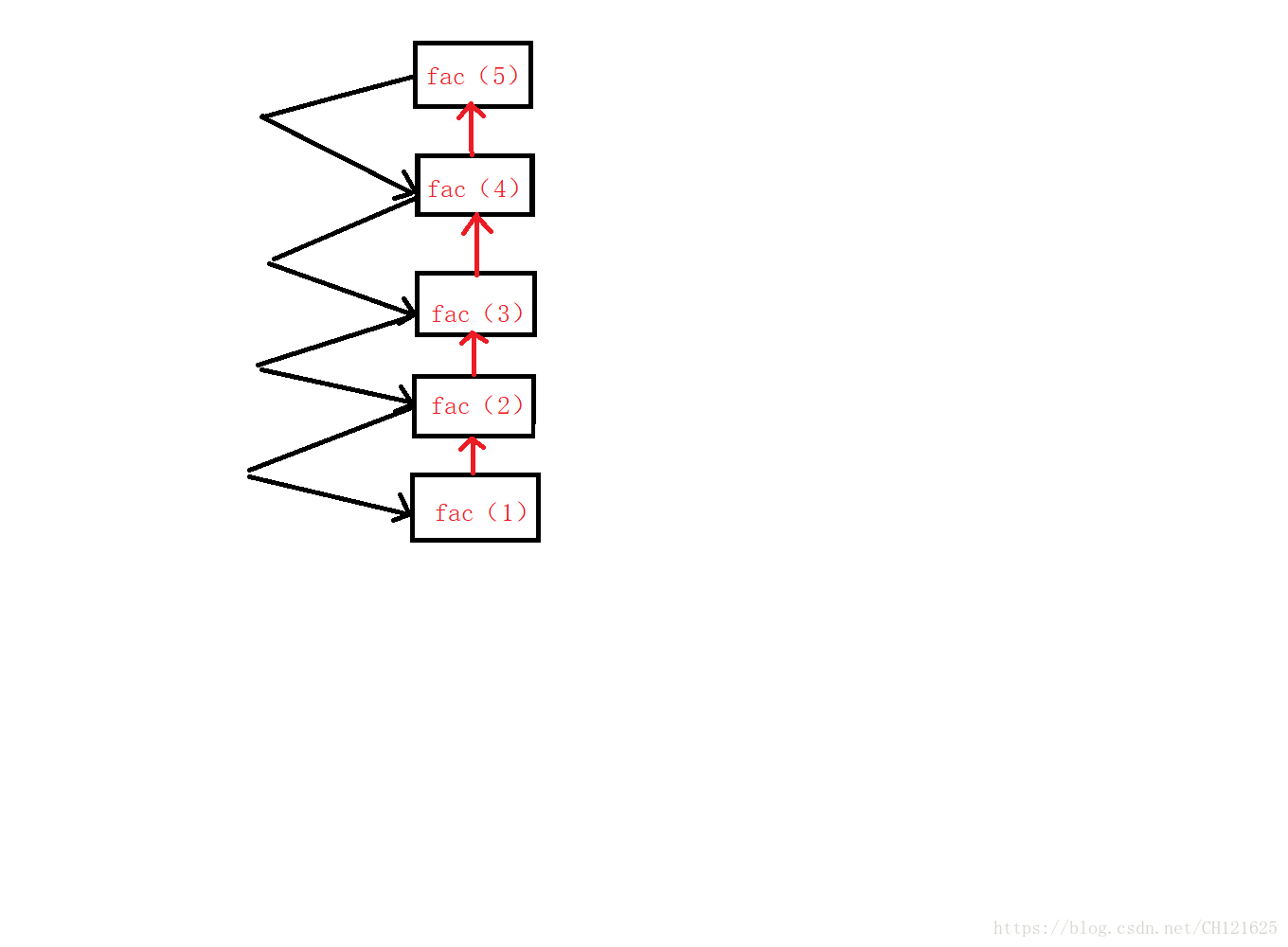
这里空间复杂度我们就可以这样来看，当我们n=5的阶乘，我们首先要算出n=4的阶乘并保存，然后知道n=4的阶乘我们必须知道n=3的阶乘并保存，知道n=3的阶乘我们就必须要知道n=2的阶乘并保存，知道n=2的阶乘我们就必须知道n=1的阶乘。这个过程我们就需要开辟n块空间来保存这些数的阶乘，多以空间复杂度为:O(n)。
这一过程如图：

菲波那切数列的递归算法：

首先来看程序：

int fib(int n)
{
    if (n <3)
    {
        return 1;
    }
    return fib(n - 1) + fib(n - 2);
}

这里计算时间复杂度时我们首先来用图来看一下当n=5时我们这个数列的求解过程：
如上图所示，我们除去最后一行就是当我们算出这个数列当n=5时，我们这个图上面元素的个数就为2^(n-2)-1,也就是我们需要循环的次数，所以时间复杂度O(2^(n-2)-1)—>O(2^n）。
空间复杂度

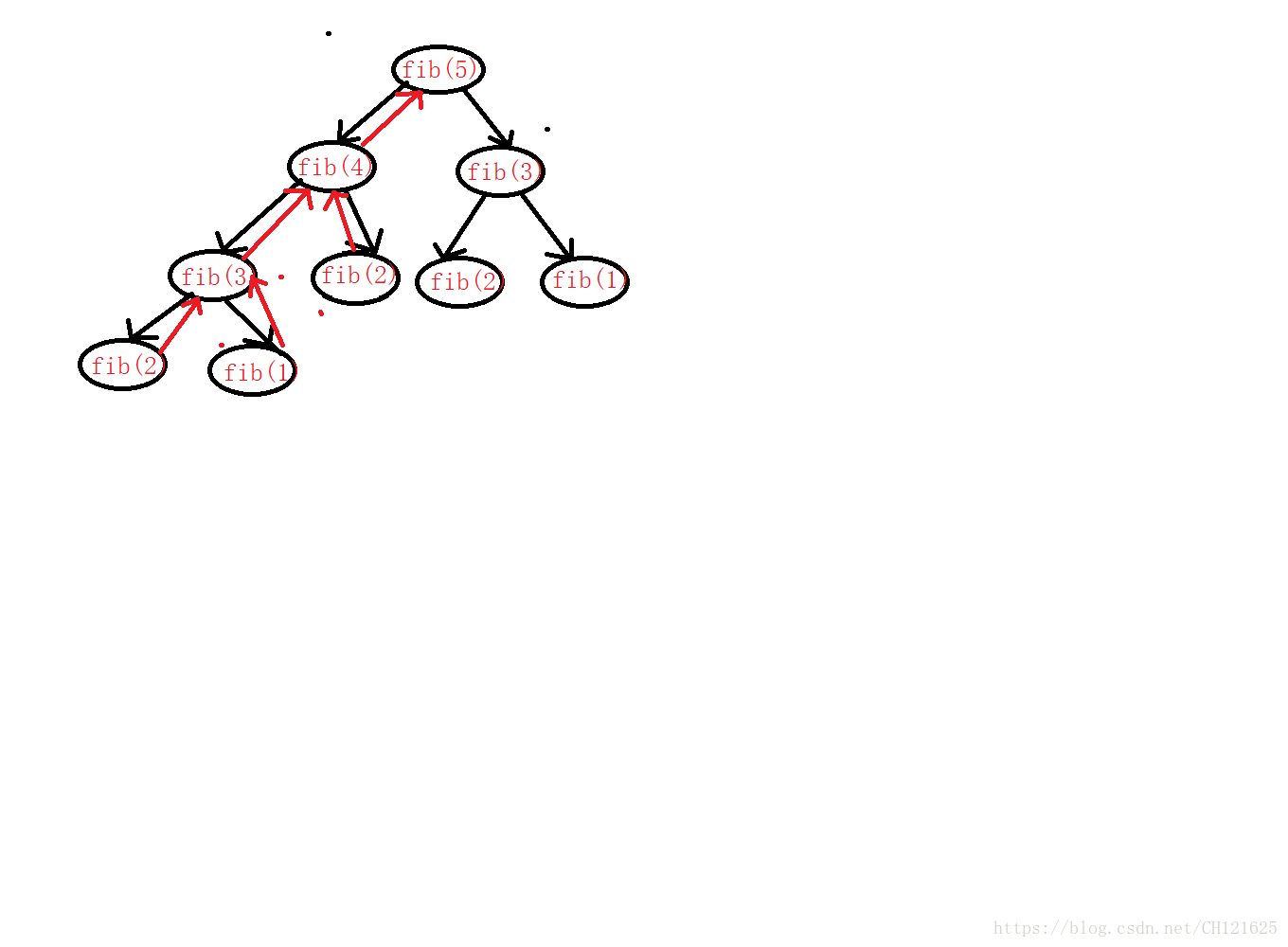
正如这张图我们看到的这就是空间复杂度的空间开辟过程，所以空间杂度为：O(n-1)—>O(n)。