矩阵论笔记:详细介绍矩阵的三角分解(LR分解)+平方根分解(Cholesky分解)!
| 详细介绍矩阵的三角分解(LR分解)+平方根分解(Cholesky分解)! |
文章目录
- 一. 三角分解(LR分解)
- 1.1. 方阵的两个重要分解
- 1.2. 上(下)三角阵的性质
- 1.3. 三角分解的概念
- 1.4. 三角分解的充要条件:定理1
- 二. 三角分解(LR分解)的求解
- 2.1. 三角分解的方法之高斯消元法
- 2.2. 带行交换的LR分解:定理2
- 2.3. 三角分解的方法之待定系数法
- 三. 平方根分解(Cholesky分解)
- 3.1. LDR分解的定义(预备知识)
- 3.2. 平方根分解(Cholesky分解)
- 3.3. 平方根分解的求解之高斯消元法
- 3.4. 平方根分解的求解之待定系数法
- 四. Cholesky分解用在计算马氏距离
- 4.1. 马氏距离
- 4.2. matlab实现计算马氏距离
- 参考文献
一. 三角分解(LR分解)
LR 分解( LR Decomposition )是矩阵分解的一种,可以将一个矩阵分解为一个单位下三角矩阵和一个上三角矩阵的乘积(有时是它们和一个置换矩阵的乘积)。LR 分解主要应用在数值分析中,用来解线性方程、求反矩阵或计算行列式。
1.1. 方阵的两个重要分解
内容回顾:
- ①是相似对角化: A = P diag { λ 1 , λ 2 , ⋯ , λ n } P − 1 \mathbf A=\mathbf P \operatorname{diag}\left\{\lambda_{1}, \lambda_{2}, \cdots, \lambda_{n}\right\} \mathbf P^{-1} A=Pdiag{λ1,λ2,⋯,λn}P−1
- ②是
Jordan标准形: A = P diag { J 1 ( λ 1 ) , J 2 ( λ 2 ) , ⋯ , J s ( λ s ) } P − 1 \mathbf A=\mathbf P \operatorname{diag}\left\{J_{1}\left(\lambda_{1}\right), J_{2}\left(\lambda_{2}\right), \cdots, J_{s}\left(\lambda_{s}\right)\right\} \mathbf P^{-1} A=Pdiag{J1(λ1),J2(λ2),⋯,Js(λs)}P−1 - 这些矩阵分解也是有问题,首先矩阵 P \mathbf P P(是由特征向量构成,它的性质我们不是很熟悉) 的性质我们不是很熟悉,当然中间的对角阵和对角块我们比较熟悉。我们希望把矩阵分解为形式比较简单或性质比较熟悉的若干个矩阵的乘积形式,这就叫做矩阵分解。
- 分解意义: 清晰地反映出原矩阵的某些特征,提供有效的数值计算方法和理论分析依据。
- 哪些矩阵我们比较熟悉呢?首先
Jordan标准形,还有分块对角阵,另外还有一种三角矩阵(上三角矩阵,下三角矩阵)。而且对角元素全为1的上三角和下三角矩阵叫做单位上三角矩阵和单位下三角矩阵。
| 上三角矩阵 | 下三角矩阵 |
|---|---|
| [ a 11 ⋯ a 1 n ⋱ ⋮ a m n ] \left[\begin{array}{ccc}{a_{11}} & {\cdots} & {a_{1 n}} \\ {} & {\ddots} & {\vdots} \\ {} & {} & {a_{m n}}\end{array}\right] ⎣⎢⎡a11⋯⋱a1n⋮amn⎦⎥⎤ | [ a 11 ⋮ ⋱ a n 1 ⋯ a n n ] \left[\begin{array}{ccc}{a_{11}} & {} & {} \\ {\vdots} & {\ddots} & {} \\ {a_{n 1}} & {\cdots} & {a_{n n}}\end{array}\right] ⎣⎢⎡a11⋮an1⋱⋯ann⎦⎥⎤ |
| 单位上三角矩阵(对角全1) | 单位下三角矩阵(对角全1) |
| [ 1 ∗ … ∗ ⋱ ⋱ ⋮ ⋱ ∗ 1 ] \left[\begin{array}{rrrr}{1} & {*} & {\dots} & {*} \\ {} & {\ddots} & {\ddots} & {\vdots} \\ {} & {} & {\ddots} & {*} \\ {} & {} & {} & {1}\end{array}\right] ⎣⎢⎢⎢⎡1∗⋱…⋱⋱∗⋮∗1⎦⎥⎥⎥⎤ | [ 1 ∗ ⋱ ⋮ ⋱ ∗ ⋯ ∗ 1 ] \left[\begin{array}{cccc}{1} \\ {*} & {\ddots} & {} \\ {\vdots} & {} & {\ddots} \\ {*} & {\cdots} & {*} & {1}\end{array}\right] ⎣⎢⎢⎢⎡1∗⋮∗⋱⋯⋱∗1⎦⎥⎥⎥⎤ |
1.2. 上(下)三角阵的性质
- 上(下)三角阵的和、差、乘积、逆仍是上(下)三角阵;
- 单位上(下)三角阵的乘积、逆仍为单位上(下)三角阵;
- 另外系数矩阵 A \mathbf A A为三角阵的非齐次线性方程组 A x = b \mathbf A \mathbf x= \mathbf b Ax=b 容易求解,也就是说如果矩阵 A \mathbf A A 为上三角矩阵或者下三角矩阵,这个方程非常容易求解(本科学过对的课程非线性方程组求解高斯消元法目的就是化成三角阵);
1.3. 三角分解的概念
- 若方阵 A \mathbf A A 可分解为 A = L R \mathbf A=\mathbf L \mathbf R A=LR 其中 L \mathbf L L 是单位下三角阵, R \mathbf R R 是上三角阵,则称 A \mathbf A A 可三角分解(或
LR分解,或Doolittle分解).
对于非齐次线性方程组 A x = b \mathbf A \mathbf x= \mathbf b Ax=b
- 若方阵 A \mathbf A A 有三角分解 A = L R \mathbf A=\mathbf L \mathbf R A=LR,刚才的方程就可以变为2个方程,令 R x = y \mathbf R \mathbf x=\mathbf y Rx=y;则 A x = b \mathbf A \mathbf x= \mathbf b Ax=b 可分解为两个非齐次线性方程组:

- 这2个方程很容易解决,首先因为 L \mathbf L L 是单位下三角矩阵,则方程 L y = b \mathbf L \mathbf y=\mathbf b Ly=b 可以变为如下:
[ 1 l 21 1 ⋮ ⋱ ⋱ l n 1 ⋯ l m n − 1 1 ] [ y 1 y 2 ⋮ y n ] = [ b 1 b 2 ⋮ b n ] \left[\begin{array}{cccc}{1} & {} & {} & {} \\ {l_{21}} & {1} & {} & {} \\ {\vdots} & {\ddots} & {\ddots} & {} \\ {l_{n 1}} & {\cdots} & {l_{m n-1}} & {1}\end{array}\right]\left[\begin{array}{c}{y_{1}} \\ {y_{2}} \\ {\vdots} \\ {y_{n}}\end{array}\right]=\left[\begin{array}{c}{b_{1}} \\ {b_{2}} \\ {\vdots} \\ {b_{n}}\end{array}\right] ⎣⎢⎢⎢⎡1l21⋮ln11⋱⋯⋱lmn−11⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡y1y2⋮yn⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡b1b2⋮bn⎦⎥⎥⎥⎤ - 其中:可以明显发现 y 1 = b 1 y_1 = b_1 y1=b1,然后可以推出 y 2 y_2 y2,以此类推! y 1 ⇒ y 2 ⇒ ⋯ ⇒ y n y_{1} \Rightarrow y_{2} \Rightarrow \cdots \Rightarrow y_{n} y1⇒y2⇒⋯⇒yn
- 再由方程组 R x = y \mathbf R \mathbf x=\mathbf y Rx=y
[ r 11 r 12 ⋯ r 1 n r 22 ⋱ r 2 n ⋱ ⋮ r n n ] [ x 1 x 2 ⋮ x n ] = [ y 1 y 2 ⋮ y n ] \left[\begin{array}{cccc}{r_{11}} & {r_{12}} & {\cdots} & {r_{1 n}} \\ {} & {r_{22}} & {\ddots} & {r_{2 n}} \\ {} & {} & {\ddots} & {\vdots} \\ {} & {} & {} & {r_{n n}}\end{array}\right]\left[\begin{array}{c}{x_{1}} \\ {x_{2}} \\ {\vdots} \\ {x_{n}}\end{array}\right]=\left[\begin{array}{c}{y_{1}} \\ {y_{2}} \\ {\vdots} \\ {y_{n}}\end{array}\right] ⎣⎢⎢⎢⎡r11r12r22⋯⋱⋱r1nr2n⋮rnn⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡x1x2⋮xn⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡y1y2⋮yn⎦⎥⎥⎥⎤ - 其中 x n = r n n x_n=r_{nn} xn=rnn,最终我们可以得到: x n ⇒ x n − 1 ⇒ ⋯ ⇒ x 1 x_{n} \Rightarrow x_{n-1} \Rightarrow \cdots \Rightarrow x_{1} xn⇒xn−1⇒⋯⇒x1
- 所以三角分解的一个很重要的应用就是用来解非齐次线性方程组,其可以简化运算。
1.4. 三角分解的充要条件:定理1
定理1:

- 先证明充要性:





- 下面证明唯一性:

- 下面证明必要性


二. 三角分解(LR分解)的求解
2.1. 三角分解的方法之高斯消元法
下面的例子1:

- 这里也是按照前一小节中证明充分性的方法。首先我们判断一下
n-1阶顺序主子式是否有0:

- 下面要用到高斯消元法,再系数矩阵的右边添加一个单位矩阵变成一个增广矩阵:
- 参考链接:增广矩阵!
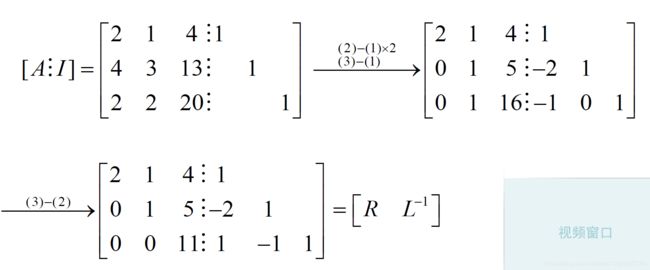
- 这里我们已经把 R \mathbf R R 算出来了就是前面的上三角矩阵,后面的是 L − 1 \mathbf L^{-1} L−1,我们只需要对 L − 1 \mathbf L^{-1} L−1 再求逆就可以得到了 L \mathbf L L;这就是第一种方法高斯消元法求解三角分解,其中有求逆相对麻烦一些。


下面的例子2:

- 不存在
LR分解,但是刚才我们介绍过三角分解主要作用就是用来求解线性方程的。解方程的时候只要这个矩阵是可逆的,肯定存在解。那么这个矩阵是可逆的,因此这个方程是有唯一解的。 - 如果我们想用三角分解求解这个方程,怎么办呢?我们发现只要把这个矩阵的第一行和第二行交换一下,矩阵 A \mathbf A A变为 A ~ \mathbf {\tilde{A}} A~,这个矩阵是满足三角分解的条件的。
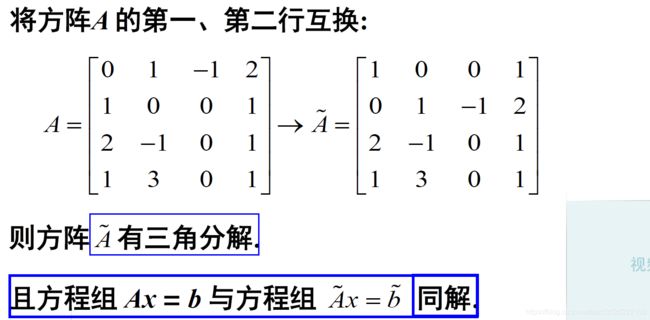
- 那么问题来了?方阵 A \mathbf A A 和 A ~ \mathbf {\tilde{A}} A~有什么关系呢?

注意: 置换矩阵就是单位阵置换行以后的矩阵。
2.2. 带行交换的LR分解:定理2
定理2:

下面的例子1:
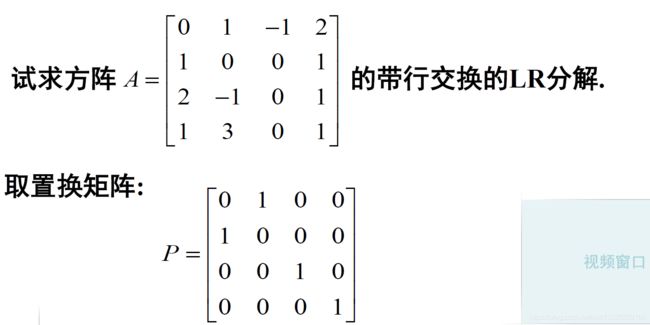

- 下面利用高斯消元法求解:



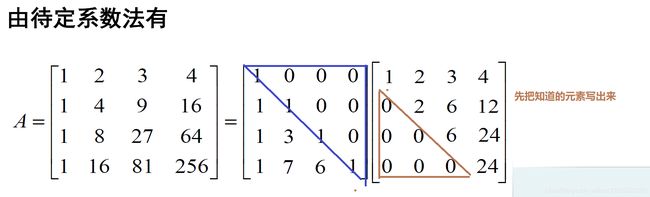
2.3. 三角分解的方法之待定系数法
通过前面的求解我们发现高斯消元法有一个问题:就是我们求解完得到的有个 L − 1 \mathbf L^{-1} L−1,我们需要转变求解其逆矩阵得到 L \mathbf L L,这样求解比较麻烦,所以编程实现也比较麻烦!


- 由矩阵的乘法可以知道, L R \mathbf L \mathbf R LR相乘的结果和 A \mathbf A A 对应位置相等。
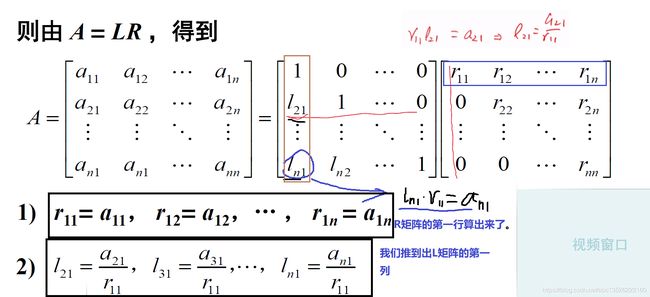
- 我们是如何推导的呢?先算 R \mathbf R R 的第一行,它和 A \mathbf A A 的第一行是一样的,算完之后我们就可以算出来 L \mathbf L L 的第一列。剩下我们再计算 R \mathbf R R 的第二行,用算 L \mathbf L L 的第二行乘以 R \mathbf R R 的第二列,得到如下的
3)和4);

- 由此得到一般的公式(这个公式看着复杂,这个公式记不住没关系,我们知道先计算 R \mathbf R R 的第一行,再计算 L \mathbf L L 的第一列,依次进行下去(记住这个顺序)… ):
r k j = a k j − ∑ i = 1 k − 1 l k i r i j , j = k , k + 1 , ⋯ , n r_{k j}=a_{k j}-\sum_{i=1}^{k-1} l_{k i} r_{i j}, \quad j=k, \quad k+1, \cdots, n rkj=akj−i=1∑k−1lkirij,j=k,k+1,⋯,n
l i k = 1 r k k ( a i k − ∑ m = 1 k − 1 l i m r m k ) , i = k + 1 , ⋯ , n l_{i k}=\frac{1}{r_{k k}}\left(a_{i k}-\sum_{m=1}^{k-1} l_{i m} r_{m k}\right), \quad i=k+1, \cdots, n lik=rkk1(aik−m=1∑k−1limrmk),i=k+1,⋯,n
下面的例子1:
- 这里我们直接用待定系数法,不用高斯消元法,当然可以用这个。

- 我们首先计算 R \mathbf R R 的第一行,我们刚才知道 R \mathbf R R 的第一行和 A \mathbf A A 的第一行是一样的。 再算 L \mathbf L L 的第一列,依次进行下去。
三. 平方根分解(Cholesky分解)
- 下面我们介绍另外一种分解叫做平方根分解,首先介绍一下预备知识LDR分解。
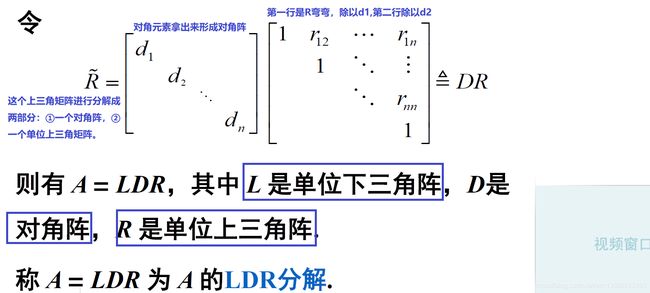
3.1. LDR分解的定义(预备知识)

- 这样得到的矩阵分解就是比较对称的了,所以怎么求LDR分解其实很简单:首先求解 A \mathbf A A 的三角分解(LR分解) A = L R \mathbf A=\mathbf L \mathbf R A=LR;然后把 R \mathbf R R 的对角元素取出来组成一个对角阵,然后 m a t h b f R mathbf R mathbfR 的每一行除以相应的对角元素。
下面的例子1:


3.2. 平方根分解(Cholesky分解)
如何矩阵 A \mathbf A A 是对称矩阵我们会得到什么结果?如果矩阵 A \mathbf A A 又是一个正定矩阵我们又会得到什么结论?这就是我们引出的平方根分解
- 正定矩阵 A \mathbf A A分解

注意: 为什么可以得到 L T = R \mathbf {L}^{\mathbf{T}}=\mathbf {R} LT=R A T = ( L D R ) T = R T D T L T = R T D L T \begin{array}{l}{\mathbf A^{T}=(\mathbf L \mathbf D \mathbf R)^{T}} = { \mathbf R^{T} \mathbf D^{T} \mathbf L^{T}} = { \mathbf R^{T} \mathbf D \mathbf L^{T}}\end{array} AT=(LDR)T=RTDTLT=RTDLT 再利用分解是唯一的 A = L D R \begin{array}{l}{\mathbf A=\mathbf L \mathbf D \mathbf R}\end{array} A=LDR 又因为 A \mathbf A A是对称矩阵,则 A = A T = L D R = R T D L T \begin{array}{l}{\mathbf A= \mathbf A^T=\mathbf L \mathbf D \mathbf R=\mathbf R^{T} \mathbf D \mathbf L^{T}}\end{array} A=AT=LDR=RTDLT所以我们可以得到: L T = R \mathbf {L}^{\mathbf{T}}=\mathbf {R} LT=R
- 有了上面的以后,我们再做一个分解,因为 D \mathbf D D 是大于0的,我们对里面的元素进行开根号,标记为 D 1 2 \mathbf D^{\frac{1}{2}} D21; D 1 2 = [ d 1 d 2 ⋱ d n ] \mathbf D^{\frac{1}{2}}=\left[\begin{array}{cccc}{\sqrt{d_{1}}} & {} & {} & {} \\ {} & {\sqrt{d_{2}}} & {} & {} \\ {} & {} & {\ddots} & {} \\ {} & {} & {} & {\sqrt{d_{n}}}\end{array}\right] D21=⎣⎢⎢⎡d1d2⋱dn⎦⎥⎥⎤
- 则有: A = L D R = L D 1 2 D 1 2 L T = ( L D 1 2 ) ( L D 1 2 ) T \begin{array}{l}{\mathbf A=\mathbf L \mathbf D \mathbf R=\mathbf L \mathbf D^{\frac{1}{2}} \mathbf D^{\frac{1}{2}} \mathbf L^{\mathrm{T}}=\left(\mathbf L \mathbf D^{\frac{1}{2}}\right)\left(\mathbf L \mathbf D^{\frac{1}{2}}\right)^{\mathrm{T}}}\end{array} A=LDR=LD21D21LT=(LD21)(LD21)T
注意: 其中 L D 1 2 \mathbf L \mathbf D^{\frac{1}{2}} LD21 是下三角矩阵。如果 A \mathbf A A 是一维的,这里直接相当于一个数字乘以另外一个数字, A \mathbf A A 就相当于开根号,所以这就叫平方根分解(类似一个非负数开根号)。
- 如果我们令 G = L D 1 2 \mathbf G=\mathbf L \mathbf D^{\frac{1}{2}} G=LD21,则 G \mathbf G G 是对角元素大于0的下三角矩阵,且 A = G G T \mathbf A=\mathbf G \mathbf G^{\mathrm{T}} A=GGT

注意: 其实平方根分解是在LDR分解的基础之上,只要是矩阵满足正定矩阵,那么LDR分解就是平方根分解。
3.3. 平方根分解的求解之高斯消元法
- 先求矩阵 A \mathbf A A 的 LDR 分解,然后对 D \mathbf D D 开根号,然后组合 L D 1 2 \mathbf L \mathbf D^{\frac{1}{2}} LD21 就得到矩阵 G \mathbf G G。
下面的例子1:

- 方法1:高斯消元法,因为如果矩阵 A \mathbf A A 的LDR分解 A = L D R \begin{array}{l}{\mathbf A=\mathbf L \mathbf D \mathbf R}\end{array} A=LDR那么则有: G = L D 1 2 = R T D 1 2 \mathbf G=\mathbf L \mathbf D^{\frac{1}{2}}=\mathbf R^{T} \mathbf D^{\frac{1}{2}} G=LD21=RTD21 因为最早求LR分解的时候,我们只求出 R \mathbf R R 后面求解的是 L − 1 \mathbf L^{-1} L−1(涉及到求解逆矩阵这里比较麻烦),所以这里我们只要求解 R \mathbf R R 就可以了。
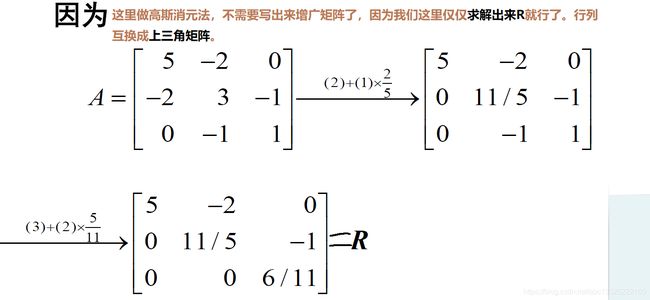
- 然后把矩阵 R \mathbf R R(上三角矩阵)分解为对角矩阵和单位上三角矩阵,就是进行LDR分解的一部分。 R = [ 5 − 2 0 0 11 / 5 − 1 0 0 6 / 11 ] = [ 5 0 0 0 11 / 5 0 0 0 6 / 11 ] [ 1 − 2 / 5 0 0 1 − 5 / 11 0 0 1 ] \mathbf R=\left[\begin{array}{ccc}{5} & {-2} & {0} \\ {0} & {11 / 5} & {-1} \\ {0} & {0} & {6 / 11}\end{array}\right]=\left[\begin{array}{ccc}{5} & {0} & {0} \\ {0} & {11 / 5} & {0} \\ {0} & {0} & {6 / 11}\end{array}\right]\left[\begin{array}{ccc}{1} & {-2 / 5} & {0} \\ {0} & {1} & {-5 / 11} \\ {0} & {0} & {1}\end{array}\right] R=⎣⎡500−211/500−16/11⎦⎤=⎣⎡500011/50006/11⎦⎤⎣⎡100−2/5100−5/111⎦⎤
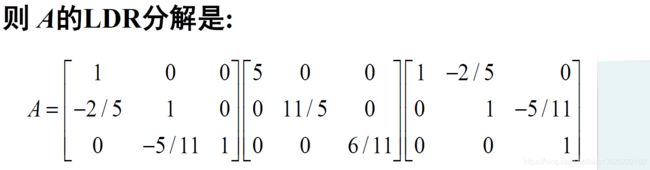
注意:这里 L \mathbf L L 为: L = [ 1 − 2 / 5 0 0 1 − 5 / 11 0 0 1 ] T \mathbf L= \left[\begin{array}{rrr}{1} & {-2 / 5} & {0} \\ {0} & {1} & {-5 / 11} \\ {0} & {0} & {1}\end{array}\right] ^{T} L=⎣⎡100−2/5100−5/111⎦⎤T
- 因此我们可以得到下三角矩阵 G = R T D 1 2 \mathbf G=\mathbf R^{T} \mathbf D^{\frac{1}{2}} G=RTD21
G = [ 1 0 0 − 2 / 5 1 0 0 − 5 / 11 1 ] [ 5 0 0 0 11 / 5 0 0 0 6 / 11 ] = [ 5 0 0 − 2 / 5 11 / 5 0 0 − 5 / 11 6 / 11 ] \begin{aligned} \mathbf G &=\left[\begin{array}{ccc}{1} & {0} & {0} \\ {-2 / 5} & {1} & {0} \\ {0} & {-5 / 11} & {1}\end{array}\right]\left[\begin{array}{ccc}{\sqrt{5}} & {0} & {0} \\ {0} & {\sqrt{11 / 5}} & {0} \\ {0} & {0} & {\sqrt{6 / 11}}\end{array}\right] \\\\ &= \left[\begin{array}{ccc}{\sqrt{5}} & {0} & {0} \\ {-2 / \sqrt{5}} & {\sqrt{11 / 5}} & {0} \\ {0} & {-\sqrt{5 / 11}} & {\sqrt{6 / 11}}\end{array}\right] \end{aligned} G=⎣⎡1−2/5001−5/11001⎦⎤⎣⎡500011/50006/11⎦⎤=⎣⎡5−2/50011/5−5/11006/11⎦⎤
- 所以 A \mathbf A A 的平方根分解(Cholesky分解)为:
A = [ 5 − 2 0 − 2 3 − 1 0 − 1 1 ] = G G T = [ 5 0 0 − 2 / 5 11 / 5 0 0 − 5 / 11 6 / 11 ] [ 5 − 2 / 5 0 0 11 / 5 − 5 / 11 0 0 6 / 11 ] \mathbf A=\left[\begin{array}{ccc}{5} & {-2} & {0} \\ {-2} & {3} & {-1} \\ {0} & {-1} & {1}\end{array}\right]=\mathbf G \mathbf G^{\mathrm{T}}=\left[\begin{array}{ccc}{\sqrt{5}} & {0} & {0} \\ {-2 / \sqrt{5}} & {\sqrt{11 / 5}} & {0} \\ {0} & {-\sqrt{5 / 11}} & {\sqrt{6 / 11}}\end{array}\right]\left[\begin{array}{ccc}{\sqrt{5}} & {-2 / \sqrt{5}} & {0} \\ {0} & {\sqrt{11 / 5}} & {-\sqrt{5 / 11}} \\ {0} & {0} & {\sqrt{6 / 11}}\end{array}\right] A=⎣⎡5−20−23−10−11⎦⎤=GGT=⎣⎡5−2/50011/5−5/11006/11⎦⎤⎣⎡500−2/511/500−5/116/11⎦⎤
3.4. 平方根分解的求解之待定系数法
- 方法2:待定系数法

- 我们可以得到如下的方程:

- 所以 A \mathbf A A 的平方根分解(Cholesky分解)为:
A = [ 5 − 2 0 − 2 3 − 1 0 − 1 1 ] = G G T = [ 5 0 0 − 2 / 5 11 / 5 0 0 − 5 / 11 6 / 11 ] [ 5 − 2 / 5 0 0 11 / 5 − 5 / 11 0 0 6 / 11 ] \mathbf A=\left[\begin{array}{ccc}{5} & {-2} & {0} \\ {-2} & {3} & {-1} \\ {0} & {-1} & {1}\end{array}\right]=\mathbf G \mathbf G^{\mathrm{T}}=\left[\begin{array}{ccc}{\sqrt{5}} & {0} & {0} \\ {-2 / \sqrt{5}} & {\sqrt{11 / 5}} & {0} \\ {0} & {-\sqrt{5 / 11}} & {\sqrt{6 / 11}}\end{array}\right]\left[\begin{array}{ccc}{\sqrt{5}} & {-2 / \sqrt{5}} & {0} \\ {0} & {\sqrt{11 / 5}} & {-\sqrt{5 / 11}} \\ {0} & {0} & {\sqrt{6 / 11}}\end{array}\right] A=⎣⎡5−20−23−10−11⎦⎤=GGT=⎣⎡5−2/50011/5−5/11006/11⎦⎤⎣⎡500−2/511/500−5/116/11⎦⎤
四. Cholesky分解用在计算马氏距离
4.1. 马氏距离
- 马氏距离度量学习的核心是获得如下式所示的马氏距离函数:
d M 2 ( x , z ) = ( x − z ) T M ( x − z ) d_{\boldsymbol M}^{2}(\boldsymbol{x}, \boldsymbol{z})=(\boldsymbol{x}-\boldsymbol{z})^{T} \boldsymbol{M}(\boldsymbol{x}-\boldsymbol{z}) dM2(x,z)=(x−z)TM(x−z) 其中 x ∈ R n \boldsymbol{x} \in \mathbb{R}^{n} x∈Rn 和 z ∈ R n \boldsymbol{z} \in \mathbb{R}^{n} z∈Rn 为 n n n 维特征空间中的 2 2 2 个样本, M ⪰ 0 \boldsymbol M \succeq 0 M⪰0 为一个 n × n n × n n×n 的对称半正定(Positive Semi-definite,PSD)矩阵。严格来说,马氏距离指代的是 d M ( x , z ) = ( x − z ) T M ( x − z ) d_{\boldsymbol M}(\boldsymbol{x}, \boldsymbol{z})=\sqrt{(\boldsymbol{x}-\boldsymbol{z})^{T} \boldsymbol{M}(\boldsymbol{x}-\boldsymbol{z})} dM(x,z)=(x−z)TM(x−z),这里实际上是马氏距离的平方。不过由于 M \boldsymbol{M} M 是一个半正定矩阵,所以 d M 2 ≥ 0 d_{\boldsymbol M}^{2}\geq 0 dM2≥0。 d M d_{\boldsymbol M} dM 比 d M 2 d_{\boldsymbol M}^2 dM2 多一次计算步骤而且对最终结果没有实质影响。因此一般将上述公式所示的函数称为马氏距离函数并用它来计算距离。 - 同时由上述公式可知,在给定样本 x \boldsymbol{x} x 和 z \boldsymbol{z} z 之后, d M 2 ( x , z ) d_{\boldsymbol M}^{2}(\boldsymbol{x}, \boldsymbol{z}) dM2(x,z) 将由矩阵 M \boldsymbol{M} M 确定,即 d M 2 ( x , z ) d_{\boldsymbol M}^{2}(\boldsymbol{x}, \boldsymbol{z}) dM2(x,z) 是由 M \boldsymbol{M} M 参数化的函数。文献中一般将矩阵 M \boldsymbol{M} M 称为度量矩阵,或简称为度量,马氏距离度量学习的核心任务即为获得具有判别性的矩阵 M \boldsymbol{M} M。
对于 n n n 维特征空间中两个样本间的马氏距离 d M ( x , z ) d_{\boldsymbol M}(\boldsymbol{x}, \boldsymbol{z}) dM(x,z) ,我们要求其需要满足以下的性质:
-
(1) d M ( x , z ) ≥ 0 ( 距 离 的 非 负 性 ) \text { (1) } d_{\boldsymbol M}(\boldsymbol{x}, \boldsymbol{z}) \geq 0 (距离的非负性) (1) dM(x,z)≥0(距离的非负性)
-
(2) d M ( x , z ) = 0 ⟺ x = z ( 同 一 性 ) \text { (2) }d_{\boldsymbol M}(\boldsymbol{x}, \boldsymbol{z})=0 \Longleftrightarrow \boldsymbol{x}=\boldsymbol{z}(同一性) (2) dM(x,z)=0⟺x=z(同一性)
-
(3) d M ( x , z ) = d M ( z , x ) ( 距 离 的 对 称 性 ) \text { (3) }d_{\boldsymbol M}(\boldsymbol{x}, \boldsymbol{z})=d_{\boldsymbol M}(\boldsymbol{z}, \boldsymbol{x})(距离的对称性) (3) dM(x,z)=dM(z,x)(距离的对称性)
-
(4) d M ( x , y ) ≤ d M ( x , z ) + d M ( z , y ) ( 距 离 三 角 不 等 式 ) \text { (4) }d_{\boldsymbol M}(\boldsymbol{x}, \boldsymbol{y}) \leq d_{\boldsymbol M}(\boldsymbol{x}, \boldsymbol{z})+d_{\boldsymbol M}(\boldsymbol{z}, \boldsymbol{y})(距离三角不等式) (4) dM(x,y)≤dM(x,z)+dM(z,y)(距离三角不等式)
-
为了使马氏距离函数满足上述各个性质,关键在于约束度量矩阵 M \boldsymbol{M} M 的半正定性,因此在马氏距离学习方法中一般都明确约束 M ⪰ 0 \boldsymbol M \succeq 0 M⪰0。另外,马氏距离与欧氏距离也存在密切的联系,如果对度量矩阵 M \boldsymbol{M} M 作 Cholesky分解有 M = L L T \boldsymbol M=\boldsymbol L \boldsymbol L^{T} M=LLT ( L (\boldsymbol L (L为下三角矩阵 ) ) )
d M 2 ( x , z ) = ( x − z ) T M ( x − z ) = tr ( M T ( x − z ) ( x − z ) T ) = ( x − z ) T L L T ( x − z ) = ( L T ( x − z ) ) T L T ( x − z ) \begin{aligned} d_{\boldsymbol M}^{2}(\boldsymbol{x}, \boldsymbol{z}) &=(\boldsymbol{x}-\boldsymbol{z})^{T} \boldsymbol{M}(\boldsymbol{x}-\boldsymbol{z}) \\&=\operatorname{tr}\left(\boldsymbol M^{T}(\boldsymbol{x}-\boldsymbol{z})(\boldsymbol{x}-\boldsymbol{z})^{T}\right) \\ &=(\boldsymbol{x}-\boldsymbol{z})^{T} \boldsymbol L \boldsymbol L^{T}(\boldsymbol{x}-\boldsymbol{z}) \\ &=\left(\boldsymbol{L}^{T}(\boldsymbol{x}-\boldsymbol{z})\right)^{T} \boldsymbol{L}^{T}(\boldsymbol{x}-\boldsymbol{z}) \end{aligned} dM2(x,z)=(x−z)TM(x−z)=tr(MT(x−z)(x−z)T)=(x−z)TLLT(x−z)=(LT(x−z))TLT(x−z) -
令 G = L T \boldsymbol G=\boldsymbol{L}^{T} G=LT,则上面的等式可以变为如下:
d M 2 ( x , z ) = [ G ( x − z ) ] T [ G ( x − z ) ] = ∥ G ( x − z ) ∥ 2 2 \begin{aligned} d_{\boldsymbol M}^{2}(\boldsymbol{x}, \boldsymbol{z}) &=\left[\boldsymbol{G}(\boldsymbol{x}-\boldsymbol{z})\right]^{T} \left[\boldsymbol G(\boldsymbol{x}-\boldsymbol{z}) \right] \\ &=\left\|\boldsymbol{G}\left(\boldsymbol{x}-\boldsymbol{z}\right)\right\|_{2}^{2} \end{aligned} dM2(x,z)=[G(x−z)]T[G(x−z)]=∥G(x−z)∥22 -
即两个特征表达向量间的马氏距离等价于使用 G \boldsymbol G G 投影后的欧氏距离。当 M \boldsymbol{M} M 为单位矩阵时,马氏距离就转化成了欧氏距离 d I 2 ( x i , z j ) = ∥ x i − z j ∥ 2 2 d_{\boldsymbol I}^{2}\left(\boldsymbol{x}_{i}, \boldsymbol{z}_{j}\right)=\left\|\boldsymbol{x}_{i}-\boldsymbol{z}_{j}\right\|_{2}^{2} dI2(xi,zj)=∥xi−zj∥22,但此时只能获得样本相同维度间的关系。
4.2. matlab实现计算马氏距离
- 测试样本971个
- 训练样本2913个

- 假设这个时候已经更新出来度量矩阵 M 100 × 100 \boldsymbol{M_{100×100}} M100×100,则可以计算马氏距离,我们可以轻易的发现计算出来的矩阵维度应该是 2913 × 971 2913×971 2913×971
function dist = MahDist(M, Xg, Xp)
% function dist = MahDist(M, Xg, Xp)
% Mahalanobis distance
Xg = Xg';
Xp = Xp';
% Input:
% <M>: the metric kernel
% <Xg>: features of the gallery samples. Size: [n, d]
% [Xp]: features of the probe samples. Optional. Size: [m, d]
%
% Note: MahDist(M, Xg) is the same as MahDist(M, Xg, Xg).
%
% Output:
% dist: the computed distance matrix between Xg and Xp
if nargin == 2 % nargin是用来判断输入变量个数的函数
D = Xg * M * Xg';
u = diag(D);
dist = bsxfun(@plus, u, u') - 2 * D;
else
u = sum((Xg * M) .* Xg, 2);
v = sum((Xp * M) .* Xp, 2);
dist = bsxfun(@plus, u, v') - 2 * Xg * M * Xp';
end
- 最终计算出来的马氏距离:
- matlab学习笔记 bsxfun函数;从计算时间上来说前两种实现差不多,远高于for的实现。但如果数据很大,第二种实现可能会有内存上的问题。所以bsxfun最好。
参考文献
- 本文主要参考国防科技大学杨文强教授课程
PPT资料,这里表示感谢!