十大排序算法——快速排序法【挖坑法、左右指针法、前后指针法和优化方式三路快排】（C语言）

快速排序法

快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略，通常称其为分治法(Divide-and-ConquerMethod)。

基本思想

从待排序序列中选取一个值作为基准值key，通过一趟排序将待排序列分割成两部分，其中一部分记录的值不大于key，另一部分记录的值不小于key，然后分别对这两部分数据继续进行排序，整个排序过程可以递归进行，以达到整个序列有序的目的。

实施基本步骤

1.选择基准值：在待排序序列中选择一个数作为基准值。
2.用基准值分割数据：把待排序序列分割成两个子区间，一个子区间数据都小于基准值，另一个子区间数据都大于基准值。
3.对分割后的子区间按1、2步继续进行排序，直到子区间个数为1（采用递归的方式进行）

选择基准值（关键字）key方式

选择待排序序列的哪个元素作为基准值是非常重要的，因为基准值影响到分割后两个子序列的长度。对于分治算法，当每次划分时，算法若都能分成两个等长的子序列时，那么分治算法效率会达到最大。总之，基准对整个算法的效率有着决定性影响，通过合理的选择基准值使排序效率增加。

1.取头尾位置

取待排序序列的第一个元素或者最后一个元素作为基准值

//选择头作为基准值
void quick_sort1(int *a,int left,int right)
{
	int key = a[left];  //选择头为基准值（首先就要和最后一个数进行）
	return key;
}
//选择尾作为基准值
void quick_sort1(int *a,int left,int right)
{
	int key = a[left];  //选择尾为基准值（首先就要和第一个数进行）
	return key;
}

如果待排序序列是一个有序或者部分有序的，用头尾作为基准值，对快排的分割是非常不利的，因为每次划分只能使待排序序列减一。此时为最坏情况失去了快速的效果。

2.随机选取基准法

取待排序序列任意元素作为基准值

 int quick_sort1(int a[],int lift,int right)
{
 	srand((unsigned)time(NULL));
	int key = rand() % (right - lift) + left;
	swap(&a[key],&a[right]);  //互换一下位置，为了调用划分函数时与上面方式下的代码保持统一
 	return a[right];
}

选取基准值的位置是随机产生的，所以分割也不会总是会出现劣质的分割，这是一种比较常见的优化方法

3.三数取中法

就是在待排序序列中取左端、中间、右端三个数，然后进行排序，将中间数作为基准值。

//用三数取中法选择基准值，对左端、中间、右端的三个数进行排序，把中间值作为基准值，放在right-1的位置
void Pick_up(int *a,int left,int right)
{
    int mid = (left+right) / 2;
    if (a[left] > a[mid])
    {
        swap(&a[left],&a[mid]);
    }
    if (a[left] > a[right])
    {
        swap(&a[left],&a[right]);
    }
    if (a[right] < a[mid])
    {
        swap(&a[right],&a[mid]);
    }
    swap(&a[right-1],&a[mid]);
}

使用三数取中法消除了待排序序列有序情况下造成的极大消耗，同时也是对随机数法下有可能出现的小概率事件的完善（当待排序序列有序的情况下随机数法仍然有可能给我们的基准是序列头尾的元素）

三种基准分治法

1.挖坑法

选择头为基准值来说，思路就是：
头为初始坑，就从右往左找第一个小于基准值的数来填初始坑，就产生了第二个坑，在从左往右找第一个大于基准值的数来填第二个坑，一次反复进行填坑，直到begin=end时，说明坑左边的数不大于key，坑右边的不小于key，就直接将key填入坑中，得到两个子区间，在用递归的方式对子区间进行上述操作。（文字看不明白可以去博客园或者其他博客看看图解方式，用数据操作一遍，我在是就省略图解步骤啦）

//挖坑法-取头为基准值
void quick_sort1(int *a,int left,int right)
{
    if (left>=right) //如果左边索引大于或等于右边得索引就代表已经整理完成了一组
    { 
        return  ;
    }
    int begin = left;
    int end = right;
    int key = a[left];  //选择头为基准值作为初始坑（首先就要和最后一个数进行）
    while (begin < end)
    {
        while (begin < end && key <= a[end])  //从右往左找第一个小于基准值的数来填key
        {
            end--;  //从右往左寻找
        }
        a[begin]=a[end];
        while (begin < end && key >= a[begin])  //从左往右找第一个大于基准值的数来填key
        {
            begin++;  //从左往右寻找
        }
        a[end]=a[begin];
        
    }
    /*当begin=end时，说明坑左边的数不大于key，坑右边的不小于key，
    就直接将key填入坑中，得到两个子区间*/
    a[begin]=key; 
    //递归操作
    quick_sort1(a,left,begin-1);   //左子区间
    quick_sort1(a,begin+1,right);  //右子区间
    
    
}

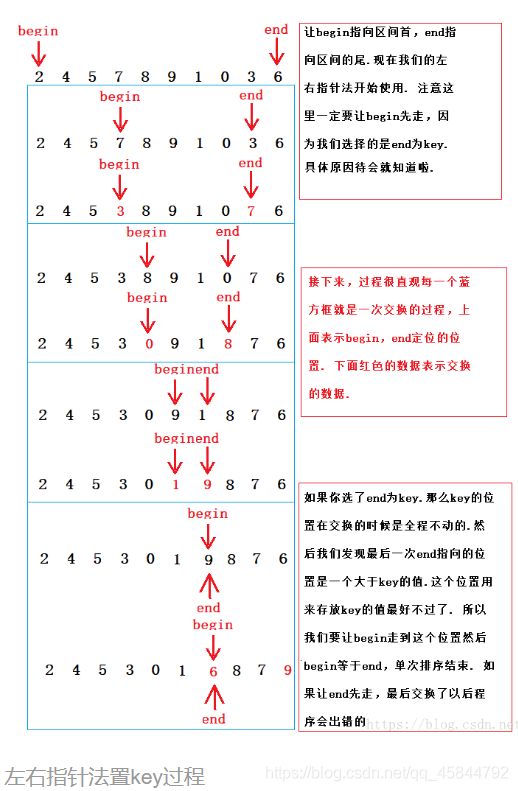
2.左右指针法

看下面这个图就明白了

//数值交换函数
void swap(int *a,int *b)
{
    int temp;
    temp = *a;
    *a = *b;
    *b = temp;
}
//左右指针法-取尾为基准值
void quick_sort2(int *a,int left,int right)
{
    if (left>=right) //如果左边索引大于或等于右边得索引就代表已经整理完成了一组
    { 
        return  ;
    }
    int key=a[right];  //取尾为基准值（先从左往右找）
    int begin = left;
    int end = right;
    while (begin < end)
    {
        while(begin < end && a[begin] <= key)   //从左往右找第一个数比key大的
        {
            begin++;
        }
        while (begin < end && a[end] >=key)  //从右往左找第一个数比key小的
        {
            end--;
        }
        swap(&a[begin],&a[end]);         //将找到的大值与小值交换 
    }
    /*当begin和end相遇时，正好就是把key与begin交换，
    使得得到两个子区间，左子区间都小于key，右区间都大于key*/
    swap(&a[begin],&a[right]);   
    //递归操作
    quick_sort2(a,left,begin-1);    //左子区间
    quick_sort2(a,begin+1,right);   //右子区间
}

3.前后指针法

基本思路：
定义两个指针，一前一后，前面指针找比基数值大的数，后面指针找比基数值小的数，前面的指针找到后，将前后指针所指向的数据交换，当前面的指针遍历完整个数组时，将基准值与后指针的后一个位置的数据进行交换，然后以后指针的后一个位置作为分界，然后将数组分开，进行递归排序。

//数值交换函数
void swap(int *a,int *b)
{
    int temp;
    temp = *a;
    *a = *b;
    *b = temp;
}
//前后指针法-取尾为基准值
void quick_sort3(int *a,int left,int right)
{
     if (left>=right) //如果左边索引大于或等于右边得索引就代表已经整理完成了一组
    { 
        return  ;
    }
    int pre = left-1;  //后指针
    int cur = left;   //前指针
    int key = a[right];  //取尾为基准值（先从前往后找）
    while (cur < right)  
    {
        /*将前指针与基准值进行比较，前指针比基准值小将后指针自增1，前指针比基准值大将后指针不变
        此时后指针与前指针相等不交换位置， 不相等前后指针交换位置*/
        if (a[cur] < key && ++pre != cur)   
        {
            swap(&a[cur],&a[pre]);    //前后指针交换位置
        }
        cur++;   //前指针向后移动
        
    }
    /*当cur==right时，pre往后移动一位，交换pre与right位置的值，
    得到两个子区间，使得左子区间值都小于pre位置的值，右子区间的值都大于pre位置的值*/
    swap(&a[++pre],&a[right]);
    //递归操作
    quick_sort3(a,left,pre-1);   //左子区间
    quick_sort3(a,pre+1,right);  //右子区间
}

三种优化方式

1.对于基准的选择按情况而定（取头尾位置、随机选取基准法、三数取中法）

对于无序的序列可用取头尾位置的
对于一个有序或者部分有序的可用随机选取基准法和三数取中法

2.三路快排

三路排序算法把排序的数据分为三部分，分别为小于key，等于key，大于key，这样三部分的数据中，等于key的数据在下次递归中不再需要排序，小于key和大于key的数据也不会出现某一个特别多的情况，通过此方式三路快速排序算法的性能更优。

适用于数据多且相等的数据多时

//数值交换函数
void swap(int *a,int *b)
{
    int temp;
    temp = *a;
    *a = *b;
    *b = temp;
}
//三路快排法
void Three_way_quick_sort(int *a,int left,int right)
{
    if (left >= right)  //如果左边索引大于或等于右边索引就代表已经整理完成一个组了
    {
        return ;
    }
    int key = a[left];  //选择left为基准
    int lt = left;  //将
    int gt = right+1;  //将>key的分界线的索引值gt初始化为最后一个元素right的后一个元素所在位置（也就是>key部分的第一个元素所在位置）
    int i = left + 1;  //将遍历序列的索引值i初始化为left+1
    while (i < gt)
    {
        if (a[i] < key)  //如果当前位置元素
        {
            swap(&a[i],&a[lt+1]);  
            lt++;  //表示
            i++;  //考虑下一个元素
        } 
        else if(a[i] > key)  //如果当前位置元素>key,则将当前位置元素与>key部分的第一个元素的前一个元素交换位置
        {
            swap(&a[i],&a[gt - 1]);  //此时i不用动，因为交换过来的元素还没有考虑他的大小
            gt--;  //表示>key部分多了一个元素
        } 
        else  //如果当前位置元素=key，则只需要将i++，表示=key部分多了一个元素
        {
            i++;
        }
        swap(&a[left],&a[lt]);  //上面的遍历完成之后，将整个序列的第一个元素（也就是基准元素）放置在合适的位置
        Three_way_quick_sort(a,left,lt-1);  //对
        Three_way_quick_sort(a,gt,right);  //对>key部分递归
         
    }
    
}

3.小区间优化可用插入排序

当快排不断递归处理子区间时，随着子区间的不断缩短，子区间数量快速增加，用快排处理这些区间很小且数量很多的子区间时，系统要为每次的函数调用分配栈帧空间，这对我们是很不利的。当待排序序列的长度分割到一定大小后，继续分割的效率比插入排序要差，此时使用插排对其优化。

//插入排序法
void Insertion_Sort(int *a,int left,int right)
{  
    if (!a)
    {
        return ;
    }
    
    if (left==right)
    {
        return ;
    }
    
    int i,j;
    for ( i = left; i <= right; i++)  //假设第一个数为有序序列，所以数组下标从一开始
    {
        int temp=a[i];    //从无序序列中取一个数为待插入数字，与有序序列中的数进行比较，找到合适的位置插入其中
        for ( j = i; j>0 && a[j-1]> temp; --j)  //判断条件为两个，j>0为数组边界判断，a[j-1]>temp为插入的判断条件
        {
            a[j]=a[j-1];
        }
        a[j]=temp;  //找到合适的位置插入其中
        
    }
}
//数值交换函数
void swap(int *a,int *b)
{
    int temp;
    temp = *a;
    *a = *b;
    *b = temp;
}
//左右指针法-取尾为基准值
void quick_sort2(int *a,int left,int right)
{
    if (left>=right) //如果左边索引大于或等于右边得索引就代表已经整理完成了一组
    { 
        return  ;
    }
    int key=a[right];  //取尾为基准值（先从左往右找）
    int begin = left;
    int end = right;
    while (begin < end)
    {
        while(begin < end && a[begin] <= key)   //从左往右找第一个数比key大的
        {
            begin++;
        }
        while (begin < end && a[end] >=key)  //从右往左找第一个数比key小的
        {
            end--;
        }
        swap(&a[begin],&a[end]);         //将找到的大值与小值交换 
    }
    /*当begin和end相遇时，正好就是把key与begin交换，
    使得得到两个子区间，左子区间都小于key，右区间都大于key*/
    swap(&a[begin],&a[right]);   
    //递归操作
    quick_sort2(a,left,begin-1);    //左子区间
    quick_sort2(a,begin+1,right);   //右子区间
}
//加入插入排序进行优化
void Insert_quick_sort(int *a,int left,int right)
{
    if (right-left<=15)
    {
        Insertion_Sort(a,left,right);
        return ;
    }
    else
    {
        quick_sort2(a,left,right);

    }
}