【CPG控制】Hopf振荡器之间的耦合

一、前情回顾

现在我们的hopf振荡器的数学模型如下：
$$\begin{array}{cc}\frac{dx}{dt}=& \alpha (\mu -r^2)x-\omega y\\ & \\ \frac{dy}{dt}=& \alpha (\mu -r^2)y+\omega x\\ & \\ r^2=& x^2+y^2\\ & \\ \omega =& \frac{\omega st}{e^{-ay}+1}+\frac{{\omega }_{sw}}{e^{ay}+1}\\ & \\ {\omega }_{st}=& \frac{1-\beta }{\beta }{\omega }_{sw}\end{array}$$

我们可以这样理解，它输出的是单个点P的位置[x，y]：

在实际使用时，该点P位置可作为机器人参考系下的位置点，也可作为关节的角度值，但是需要根据实际情况进行一系列变换，往后我们会讨论这个问题，现在我们先把目光集中在hopf振荡器本身。

1、北理大的CPG控制网络

四足机器人，顾名思义，有四条腿，不考虑横向的髋关节的话我们仍有8个自由度，因此也就需要8个控制指令，而我们的振荡器有2个输出值，所以，我们需要使用4个hopf振荡器，分别对应每一条腿。

强调一下，这种方法是北京理工大学《仿生四足机器人技术》里面提出的CPG控制网络模型，这在我的第一篇文章里面也已经介绍过了

我们将各腿关系整理一下，这里将各个振荡器的x值作为髋关节的角度值，y值作为膝关节的角度值，如下图：

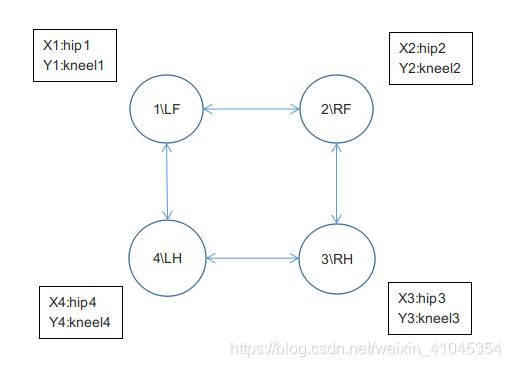
各腿的相位图：

整理之后的数学模型，我们写成微分方程的形式，其实就是在之前的模型上加入了一个耦合项：
$$\frac{d{x}_i}{dt}=\alpha (\mu -r_i^2)x_i^2-{\omega }_i{y}_i+\sum _{j=1}^4(\cos {\theta }_j^i{x}_j-\sin {\theta }_j^i{y}_j)$$

$$\frac{d{y}_i}{dt}=\alpha (\mu -r_i^2)y_i^2+{\omega }_i{x}_i+\sum _{j=1}^4(\sin {\theta }_j^i{x}_j+\cos {\theta }_j^i{y}_j)$$

其中，$i=1,2,3,4$，分别表征各条腿对应的id，${\theta }_j^i=2\pi ({\phi }_i-{\phi }_j)$

关于耦合项无效问题

我们设定相位关系为，phase = [0, 0.5, 0.25, 0.75]，
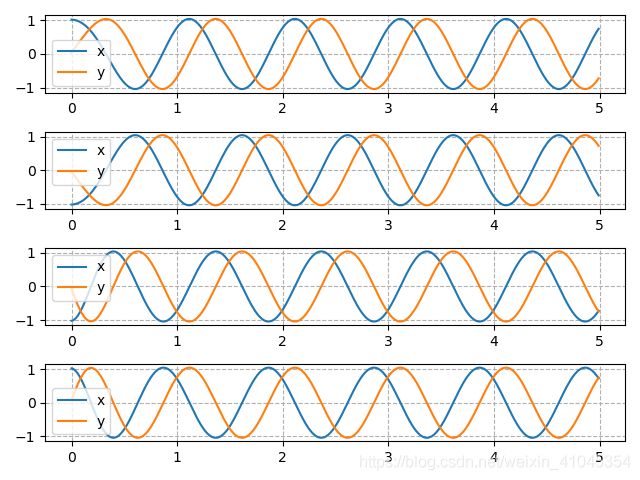
经过我的多次试验，耦合项会在某些情况下无效，这其实跟初始值有关，例如，当我们设P0_ = [1, 1, 1, 1, 0, 0, 0, 0]，我们得到的曲线会是如下：

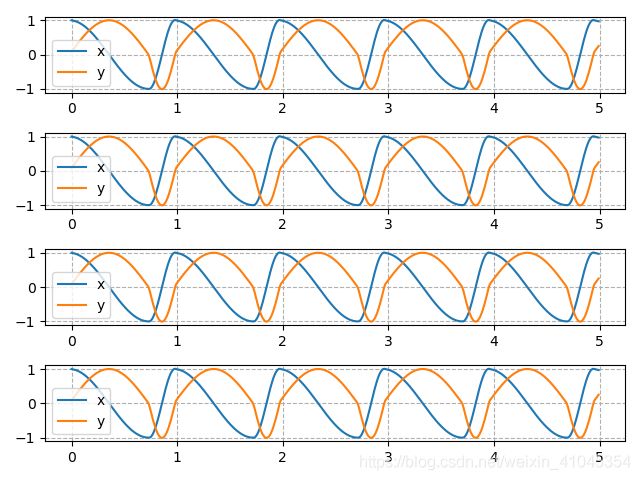
在上面这种情况下，可以看出输出信号其实是一致的，当我们把初始值设为P0_ = [1, -1, -1, 1, 0, 0, 0, 0]，我们得到的曲线会是如下，此时满足相位关系。：

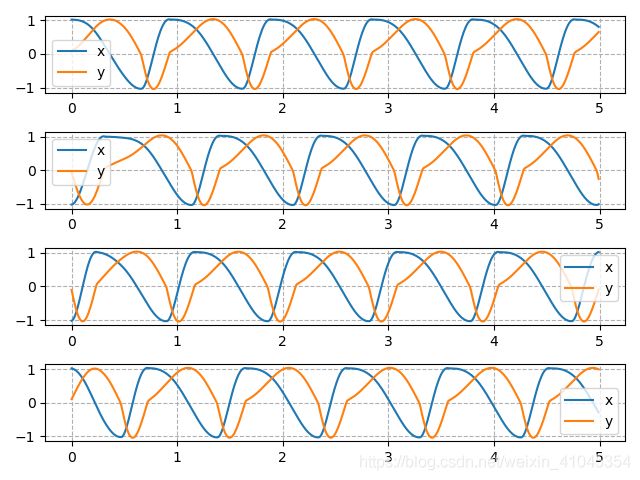
为了便于观察，我们将$\beta$设为0.5（其余参数均保持一致），相位关系仍然是phase = [0, 0.5, 0.25, 0.75]， 初始值仍为P0_ = [1, -1, -1, 1, 0, 0, 0, 0]

我把核心代码放在这，大家可以自行试验：

• hopf振荡器核心：

def hopf(pos, steps):
    x1, x2, x3, x4, y1, y2, y3, y4 = pos
    alpha, mu, beta, omega_sw = get_parms()
    omega_st = ((1 - beta) / beta) * omega_sw
    T = np.pi / omega_st + np.pi / omega_sw
    x = np.array([x1, x2, x3, x4])
    y = np.array([y1, y2, y3, y4])

    r = x ** 2 + y ** 2

    omega = omega_st / (np.e ** (-50*y) + 1) + omega_sw / (np.e ** (50*y) + 1)
    r_x, r_y = get_r(x, y)
    dx = alpha * (mu - r) * x - omega * y + r_x
    dy = alpha * (mu - r) * y + omega * x + r_y
    temp = np.hstack((x+dx*steps, y+dy*steps))

    return temp

参数：

def get_parms():
    alpha = 50
    mu = 1
    beta = 0.5
    omega_sw = 2*np.pi
    return [alpha, mu, beta, omega_sw]

耦合项：

def get_theta():
    theta = np.zeros([4, 4])
    for i in range(4):
        for j in range(4):
            theta[i, j] = (phase[i] - phase[j])
    return 2 * np.pi * theta


def get_r(x, y):
    r_x = np.zeros([4, 4])
    r_y = np.zeros([4, 4])
    theta = get_theta()
    for i in range(4):
        for j in range(4):
            r_x[i, j] = np.cos(theta[i, j])*x[j] + np.sin(theta[i, j])*y[j]
            r_y[i, j] = -np.sin(theta[i, j])*x[j] + np.cos(theta[i, j])*y[j]
    return np.sum(r_x, axis=1), np.sum(r_y, axis=1)

2、基于坐标变换（试验）

这种方法只是应用于对称信号，因此不是完善的方法

我们在前面已经强调过一个很重要的概念，我们可以把hopf振荡器输出值当做是一个点的坐标。我们以三角函数距离说明，点P1位置[x,y]跟时间有以下关系：
$$\{\begin{array}{c}x=\sin (t)\\ y=\cos (t)\end{array}$$

它的运动是这样的：

现在多加一个点P2，让其与P1的连线穿过圆心（即，在P1对面），该如和表示该点的运动呢？

答案很简单，让P1绕圆心旋转180°就行了，也就是说P2点的角度适终与P1相差$\pi$。放到整个时间线上来说就是，我们对P1点每一时刻的位置信号进行旋转变换得到P2点的信号。

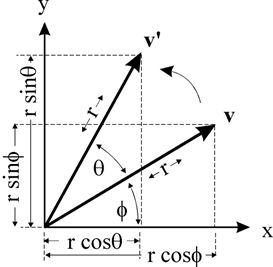
通过公式表示如下：

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$
让$\theta =\pi$计算得到点

P2点的运动曲线：

我们可以不断地对P1点的信号作变换得到新的信号，而且相位由旋转角度$\theta$决定。

---

如果觉得ok，点个赞，点个关注，也欢迎给个打赏支持一下编者的工作