CodeForces 1307 A-E
CF 1307 A-D
A Cow and Haybles 题目链接
题目描述
有n个数, 每次可以选相邻的两个数i, j: 使得ai+1, aj-1, 问经过这样d次操作后, a1最大是多少。
题目思路
首先明白题意, 是任意的两个数+1, -1, 而且又要使得a1最大, 所以, 我们可以在这d次时间内, 尽量让a1 每次都加1, 那么相邻的a2-1, 那么如果a2 等于0了呢, 那就让a3-1, 再让a2+1, 再让a1+1, a2-1, 所以, 我们发现, 从a2移到a1需要1步, a3移到a1需要2步, ai移到a1需要i-1步, OK , GET到点了!!!
注意, 不能一下子把一个数全移过去, 只能一个一个移, 因为你有可能在移的过程中就超过d次了。。。。
代码
#include
#includeB Cow and Friend 题目网址
题目描述
贝茜有太多朋友了。因为她是所有人最喜欢的牛。她的朋友兔兔在试着跳到贝茜所在的地方,那么他们就可以玩了。
更具体地,兔兔他想跳几步使得他能从(0,0)跳到 (x,0)。他只想着在二维平面上从一个点跳到另一个点当且仅当两个点的欧几里得距离是他n个喜欢的数中的其中一个,也就是 a 1 , a 2 . . . . . . . . . a n a_1, a_2.........a_n a1,a2.........an.
兔兔最少要跳几步才能从(0,0)跳到(x, 0)呢?兔兔不必跳到一个整数的坐标,换句话说,他可以跳到一个不是整数的坐标。可以证明,兔兔总可以到达他的终点。
重新在此声明,两个点的欧几里得距离可以使用公式算出,设两个点的坐标分别为 (x1,y1), (x2, y2), 那么有公式 ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2} (x1−x2)2+(y1−y2)2
如下图所示,如果兔兔喜欢的数是1和3的话,那么他可以跳两步从(0,0)
跳到(4,0)。

图中的就是样例的第一个测试的示意图,两次跳的距离都是3 ———一个兔兔喜欢的数。换句话说,每一次兔兔都会选一个数 ai然后任意地跳到一个与这个点距离为ai的地方, 相同的数可以使用多次。
题目思路
贪心
首先明白一件事情, 他让走最少的步数, 那么肯定是用最大的距离去走, 所以, 答案为ceil(x / maxn)
真的那么简单嘛??
看下面几种情况:
1) x % i == 0;
那么答案就是x / ai, 加入比较行列。
2) 最大步长大于x, 那么, 答案一定是二, 如图:
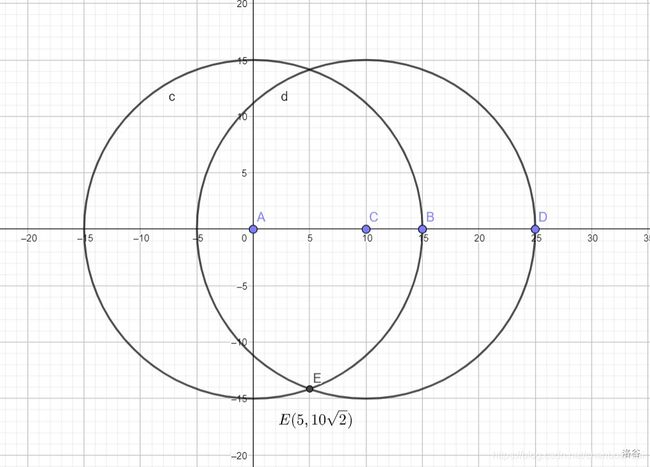
以起点为圆心作⚪, 与终点为圆心做⚪, 都已最大步长为半径为交点,就是跳到的间接点, 显而易见, 跳两步就能到终点。
到这儿, 应该就讲完了, 但我想再稍微的拓展一下, 如果最大步长小于x的话,可见按上面的那种做法两圆根本交不到。 我们可以让起点向x轴上先跳到(最大步长, 0)这个点在作⚪, 如果还交不到, 那么就在往右跳。直到能交到为止。
代码
#include
#includeC Cow and message. 题目网址
题目描述
贝茜刚刚截取了来自约翰发送出去的讯息!但是,贝茜很肯定里面一定有隐藏的讯息。
讯息是一个字符串 s s s, 全部都是由小写拉丁字母字符构成。她认为一个字符串 t t t是隐藏的当且仅当 t t t是 s s s的子序列, 且 t t t在 s s s下标中构成了一个等差数列, 公差必须为一个正整数
。例如,字符串aab是隐藏在字符串aaabb因为aab出现在 s s s的下标是1,3,5.
这刚好构成了一个等差数列,而公差是 2.贝茜觉得秘密讯息讯息一定是隐藏最多次的那一个字符串两个 s s s 中的子序列是不同的当且仅当两个字符串在 s s s中出现的下标是不同的。 请帮贝茜找出秘密讯息在 s s s中出现的次数吧。
题目思路
首先明白:秘密信息一定是有一个或两个。
证明, 首先要知道子字符串在这里指的是什么
显而易见, 我们可以看到, 这个字串里的字符位置一定是形成公差数列的。
再来考虑三个字符串的情况。
假如abc, 你会发现:当确定ab的所有情况时, c已经确定了, 因为有公差。比如a和b的公差时3, 那么这种情况在ab这个字符串里面就已经包含了, 然而在abc三个字符串里面你还要判断在b后面三个位置的字母是否是c, 如果是才算到字符串abc里, 所以就得出了这样一个结论:
三个字母的出现了,两个字母也出现了,两个字母出现了,三个字母不一定出现。
多的以此类推。
一个和两个字串就不同。
因为在两个子串里的时候,假如你要选第二个字母。你会发现公差还没有确定, 所以设要找的字串为a,b,那么a就可能和后面任意一个b去组合。
这就是和三个的区别, 因为你在找第三个的时候,前面两个已经确定了公差, 所以你不能和后面的c随意组合了。。。
说了这么多, 总之, 只要取一个和两个字符串里面出现次数的最大值就可以了吧。。。
用sufij表示维护一个后缀:从i位置到第n个位置有多少个字母j。
那么一个字母a的出现次数就为suf【1】【a】;
设ans【i】【j】表示字串为ij时出现个数。
代码
#include
#include我是不会告诉你们我没A的 逃)
D Cow and Fields 题目网址
题目描述
给定一个有 n n n个节点 m m m条边的有向图,一个顶点集 S S S.
你需要选择两个顶点 u , v ( u ≠ v , v ∈ S , u ∈ S ) u,v(u \neq v, v\in S, u \in S) u,v(u=v,v∈S,u∈S)并连接这两个顶点(允许
u , v u, v u,v之间已经有连边),求连接后从顶点1到顶点 n n n最短路的最大值.
注意:该操作只能进行一次
保证给定的图联通。
题目思路
设答案两个要添边的点为i,j。则最短路经过他俩, 那么最短路的长有两种
首先设他俩到点1, n的距离分别为dis1x, dis1y, dis2x, dis2y。
则答案为 m a x s i z e ( m i n ( d i s 1 x + d i s 2 y + 1 , d i s 1 y + d i s 2 x + 1 ) ) maxsize(min(dis1x+dis2y+1, dis1y+dis2x+1)) maxsize(min(dis1x+dis2y+1,dis1y+dis2x+1))
可见是个贪心, 那么化简: m a x s i z e ( m i n ( d i s 1 x + d i s 2 y , d i s 1 y + d i s 2 x ) ) maxsize(min(dis1x+dis2y, dis1y+dis2x)) maxsize(min(dis1x+dis2y,dis1y+dis2x))
设前面的小于后面的
最终得: d i s 1 x − d i s 1 y < d i s 2 x − d i s 2 y dis1x - dis1y \lt dis2x - dis2y dis1x−dis1y<dis2x−dis2y
就按这个贪;在维护第i到n个点dis2的最大值。
这题我也没过, 但还是要坚强的贴代码::
代码
#include
#include小结:
上次洛谷二月月赛T4我又有新思路了, 去看一看吧。