洛谷1216 数字三角形【dp】
经典例题:洛谷P1216 数字三角形
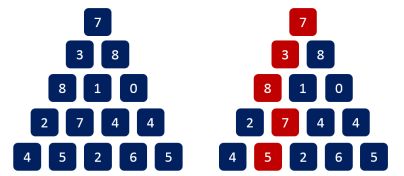
写一个程序来查找从最高点到底部任意处结束的路径,使路径经过数字的和最大。
每一步可以走到左下方的点也可以到达右下方的点。
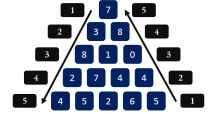
下图的黑色三角形是我们记忆化搜索的路径,我们想想,是不是可以不通过记忆化搜索就能得到这个黑色三角形??
最优性:设走到某一个位置的时候,它达到了路径最大值,那么在这之前,它走的每一步都是最大值。
-考虑这条最优的路径:每一步均达到了最大值
最优性的好处:要达到一个位置的最优值,它的前一步也一定是最优的。
-考虑图中位置,如果它要到达最优值,有两个选择,从左上方或者右上方的最优值得到:
所以从这里,定义动态规划(DP):只记录状态的最优值,并用最优值来推导出其他的最优值。
记录 F[i][j] 为第 i 行第 j 列的路径最大值,有两种方法可以推导:(两个分支两种状态,选取最大)
@顺推:用 F[i][j] 来计算 F[i+1][j],F[i+1][j+1]。用当前项去计算后面的。“我这个状态的下一步去哪里”
@逆推:用 F[i-1][j],F[i-1][j-1] 来计算 F[i][j]。用前面的来计算当前项。“从什么状态可以到达我这里”(还没想好谁到谁)
这两种思考方法也是动态规划中最基本的两种方法,解决绝大部分DP我们都可以采用这样的方法。
//T2:数字金字塔-顺推(有点类似于记忆化搜索的思路)
//d数组储存顺序:记录从顶端向底部走的路径最优值(自顶向下)
#include
#include
using namespace std;
int a[1005][1005];//储存数塔
int d[1005][1005];//从该点到底端的最大数字和
int main()
{
int i,j,n,ans;
while(cin>>n)
{
memset(d,-1,sizeof(d));
for(i=0;i>a[i][j];
}
d[0][0]=a[0][0];
for(int i=0;i //数字金字塔-逆推
//d数组储存顺序:记录从顶端向底部走的路径最优值(自顶向下)
#include
#include
using namespace std;
int a[1005][1005];//储存数塔
int d[1005][1005];//从该点到底端的最大数字和
int main()
{
int i,j,n,ans;
while(cin>>n)
{
memset(d,-1,sizeof(d));
for(i=0;i>a[i][j];
}
//逆推(自顶向下)
d[0][0]=a[0][0];
for(int i=1;i *转移方程:最优值之间的推导公式。
@顺推:
F[i+1][j] = MAX (F[i][j] + a[i+1][j]);
F[i+1][j+1] = MAX (F[i][j] + a[i+1][j+1]);
@ 逆推:
F[i][j] = MAX (F[i-1][j], F[i-1][j-1]) + a[i][j]; (注意!逆推时要注意边界情况! )
顺推和逆推本质上是一样的(复杂度一致);顺推和搜索的顺序类似;
而逆推则是将顺序反过来;顺推考虑的是“我这个状态的下一步去哪里” ,逆推的考虑的是“从什么状态可以到达我这里” 。
同时在转移的过程中我们要时刻注意边界情况。
----------------------------------------------------------------------------------------------------------------------------------
我们还可以改变搜索顺序为自底向上(下面这两个算法基本一样,写法不一样):
//数字金字塔-逆推
//改变顺序:记录从底部向上走的路径最优值(自底向上)
//和之前的逆推区别:这样较自顶向下不需要判断边界,更加简单
#include
#include
using namespace std;
int a[1005][1005];//储存数塔
int d[1005][1005];//从该点到底端的最大数字和
int main()
{
int i,j,n,ans;
while(cin>>n)
{
memset(d,-1,sizeof(d));
for(i=0;i>a[i][j];
}
d[0][0]=a[0][0];
for(int j=0;j=0;i--)
for(int j=0;j<=i;j++)
d[i][j]=a[i][j]+max(d[i+1][j+1],d[i+1][j]);//当前的+当前[i][j]左下方和右下方取较大
//答案在金字塔顶端
ans=d[0][0];
cout< //(自底向上)
#include
#include
using namespace std;
int a[1005][1005];
int d[1005][1005];
int i,j,n,t;
int dp(int i,int j)
{
if(d[i][j]>=0)
return d[i][j];
else
//写错了return d[i][j]+= a[i][j]+max(d[i+1][j],d[i][j+1]);
{
d[i][j]=a[i][j]+(i==n?0:max(dp(i+1,j),dp(i+1,j+1)));//(i==n-1? 也能AC
return d[i][j];
}
}
int main()
{
// int n; 有这个会导致样例输出7
while(cin>>n)
{
memset(d,-1,sizeof(d));
for(i=0;i>a[i][j];
}
// 两种输出方式
// dp(0,0);
// cout< *转移顺序:最优值之间的推导顺序
一个小问题:在数字金字塔中,为什么能够使用动态规划 呢??答:因为有明确的顺序: 自上而下 ,也就是说,能划分成不同的阶段,这个阶段是逐步进行的,这和搜索顺序也是类似的,所以,只要划分好阶段, 从前往后推,与从后往前推都是可以的
转自:http://www.cnblogs.com/geek-007/p/7197045.html