分支定界法——0-1背包问题

问题描述：

给定n种物品和一背包。物品i的重量是wi，其价值为vi，背包的容量为C。问:应如何选择装入背包的物品，使得装入背包中物品的总价值最大?

算法设计分析：

和回溯法中的界定函数类似，对每一个活动节点N，计算收益的上限maxPossibleProfitInSubtree，使得以N为根的子树中，任何一个节点的收益都不可能超过这个值。

活动节点使用大根堆maxHeap，按需构造解空间树——子集树。

大根堆元素heapNode结构： 

upperProfit  //以该节点为根的子树中任一节点的收益上限 

profit       //该节点目前的收益值 

weight       //该节点目前的重量 

level        //该节点在解空间树的层数 

liveNode     //指向解空间树的节点(树的节点数据成员包括： 

             // 指向父节点的parent指针和布尔类型leftChild，当且仅当此节点是左孩子时为true)

节点按其upperProfit值从大根堆中取出。

算法步骤：

1、将背包装载对象按收益密度递增顺序排序； 

2、检查左孩子节点，若左孩子可行（左孩子的目前重量小于总的capacity），向大根堆中添加此节点； 

3、检查右孩子节点，当且仅当右孩子的maxPossibleProfitInSubtree值大于目前的最大收益时，右孩子可行，将右孩子加入大根堆； 

4、从大根堆中取出一个新元素（upperProfit值最大的节点），重复2、3步骤直到最后一层节点； 

5、沿着最后一个节点到根节点路径构造最佳0/1背包解。

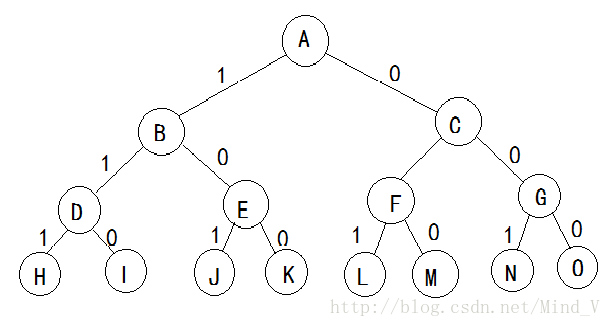
例如：0/1背包问题，当n=3时，w={20,15,15}, p={40,25,25}, c=30。收益密度{2, 5/3, 5/3}。大根堆分支界定法：收益大的优先。

队列中的元素：{}—>{A}—>{B,C}—>{C，D，E}—>{C，E}—>{C，J，K}—>{C}—>{F，G}—>{G，L，M}—>{G，M}—>{G}—>{N，O}—>{O}—>{}

C++实现

解空间树的节点结构：

struct bbNode
{
   // data members
   bbNode* parent;        // pointer to parent node
   bool leftChild;        // true iff left child of parent

   // constructor
   bbNode(bbNode* theParent, bool theLeftChild)
   {
      parent = theParent;
      leftChild = theLeftChild;
   }
};

大根堆的元素类型：

struct heapNode
{
   // data members
   bbNode* liveNode;
   double upperProfit;
   double profit;
   double weight;
   int upperWeight;    // upper weight of live node
   int level;          // level of live node

   // constructors
   heapNode() {};

   heapNode(bbNode* theLiveNode, double theUpperProfit, 
      double theProfit, double theWeight, int theLevel)
   {
      liveNode = theLiveNode;
      upperProfit = theUpperProfit;
      profit = theProfit;
      weight = theWeight;
      level = theLevel;
   }

   operator<(const heapNode right)
      {return upperProfit < right.upperProfit;}

   // type conversion to enable arithmetics etc.
   operator double() {return upperProfit;}
};

算法程序：

// global variables
double capacity;
int numberOfObjects;
double *weight;
double *profit;
double weightOfCurrentPacking;
double profitFromCurrentPacking;
int *bestPackingSoFar;
maxHeap liveNodeMaxHeap;

double maxProfitBBKnapsack()
{// Max-profit branch-and-bound search of solution space tree.
 // Set bestPackingSoFar[i] = 1 iff object i is in knapsack in best filling.
 // Return profit of best knapsack filling.
   // initialize for level 1 start
   bbNode* eNode = NULL;
   int eNodeLevel = 1;
   double maxProfitSoFar = 0.0;
   double maxPossibleProfitInSubtree = profitBound(1);

   // search subset space tree
   while (eNodeLevel != numberOfObjects + 1)
   {// not at leaf
      // check left child
      double weightOfLeftChild = weightOfCurrentPacking
                                 + weight[eNodeLevel];
      if (weightOfLeftChild <= capacity)
      {// feasible left child
         if (profitFromCurrentPacking + profit[eNodeLevel]
             > maxProfitSoFar)
            maxProfitSoFar = profitFromCurrentPacking 
                             + profit[eNodeLevel];
         addLiveNode(maxPossibleProfitInSubtree,
                     profitFromCurrentPacking + profit[eNodeLevel],
                     weightOfCurrentPacking + weight[eNodeLevel],
                     eNodeLevel + 1, eNode, true);
      }
      maxPossibleProfitInSubtree = profitBound(eNodeLevel + 1);

      // check right child
      if (maxPossibleProfitInSubtree >= maxProfitSoFar)
         // right child has prospects
         addLiveNode(maxPossibleProfitInSubtree,
                     profitFromCurrentPacking,
                     weightOfCurrentPacking,
                     eNodeLevel + 1, eNode, false);

      // get next E-node, heap cannot be empty
      heapNode nextENode = liveNodeMaxHeap.top();
      liveNodeMaxHeap.pop();
      eNode = nextENode.liveNode;
      weightOfCurrentPacking = nextENode.weight;
      profitFromCurrentPacking = nextENode.profit;
      maxPossibleProfitInSubtree = nextENode.upperProfit;
      eNodeLevel = nextENode.level;
   }

   // construct bestPackingSoFar[] by following path
   // from eNode to the root
   for (int j = numberOfObjects; j > 0; j--)
   {
      bestPackingSoFar[j] = (eNode->leftChild) ? 1 : 0;
      eNode = eNode->parent;
   }

   return profitFromCurrentPacking;
}

double knapsack(double *theProfit, double *theWeight, int theNumberOfObjects, double theCapacity, int *bestPacking)
{// theProfit[1:theNumberOfObjects] is array of object profits
 // theWeight[1:theNumberOfObjects] is array of object weights
 // theCapacity is knapsack capacity
 //  bestPacking[1:theNumberOfObjects] is set to best knapsack filling.
 // Return profit of best filling.
   capacity = theCapacity;
   numberOfObjects = theNumberOfObjects;

   // define an element array for profit densities
   element *q  = new element [numberOfObjects];

   // set up densities in q[0:numberOfObjects-1] and
   // sum the weights and profits
   double weightSum = 0.0;         // will be sum of weights
   double profitSum = 0.0;         // will be sum of profits
   for (int i = 1; i <= numberOfObjects; i++)
   {
      q[i - 1] = element(i, theProfit[i] / theWeight[i]);
      profitSum += theProfit[i];
      weightSum += theWeight[i];
   }

   if (weightSum <= capacity)   // all objects fit
   {
      fill(bestPacking + 1, bestPacking + numberOfObjects + 1, 1);
      return profitSum;
   }

   // sort into increasing density order
   sort(q, q + numberOfObjects);

   // initialize globals
   profit = new double [numberOfObjects + 1];
   weight = new double [numberOfObjects + 1];
   for (int i = 1; i <= numberOfObjects; i++)
   {// profits and weights in decreasing density order
      profit[i] = theProfit[q[numberOfObjects - i].id];
      weight[i] = theWeight[q[numberOfObjects - i].id];
   }
   weightOfCurrentPacking = 0.0;
   profitFromCurrentPacking = 0.0;
   bestPackingSoFar = new int [numberOfObjects + 1];

   // find best profit and construct packing
   double maxProfit = maxProfitBBKnapsack();
   for (int i = 1 ; i <= numberOfObjects; i++)
      bestPacking[q[numberOfObjects - i].id] = bestPackingSoFar[i];
   return maxProfit;
}

添加节点addLiveNode( )：

void addLiveNode(double upperProfit, double theProfit,
                 double theWeight, int theLevel, bbNode* theParent,
                 bool leftChild)
{// Add a new live node to the max heap.
 // Also add the new node to the solution space tree.
 // upperProfit = upper bound on profit for the live node.
 // theProfit = profit of new live node.
 // theWeight = weight of new live node.
 // theLevel = level of live node.
 // theParent = parent of new node.
 // leftChild is true iff new node is left child of theParent.
   // create the new node of the solution space tree
   bbNode* b = new bbNode(theParent, leftChild);

   // put corresponding heap node into max heap
   liveNodeMaxHeap.push(heapNode(b, upperProfit, theProfit,
                                 theWeight, theLevel));
}

界定函数profitBound()：

double profitBound(int currentLevel)
{// Bounding function.
 // Return upper bound on value of best leaf in subtree.
   double remainingCapacity = capacity - weightOfCurrentPacking;
   double profitBound = profitFromCurrentPacking;

   // fill remaining capacity in order of profit density
   while (currentLevel <= numberOfObjects &&
          weight[currentLevel] <= remainingCapacity)
   {
      remainingCapacity -= weight[currentLevel];
      profitBound += profit[currentLevel];
      currentLevel++;
   }

   // take fraction of next object
   if (currentLevel <= numberOfObjects)
      profitBound += profit[currentLevel] / 
      weight[currentLevel] * remainingCapacity;
   return profitBound;
}

大根堆的部分源码maxHeap.h：

// heap implementation of a max priority queue
// derives from the ADT maxPriorityQueue

#ifndef maxHeap_
#define maxHeap_

#include 
#include 

using namespace std;

template<class T>
void changeLength1D(T*& a, int oldLength, int newLength)
{
   if (newLength < 0)
   {
       cout << "new length must be >= 0" << endl;
       exit(1);
   }

   T* temp = new T[newLength];              // new array
   int number = min(oldLength, newLength);  // number to copy
   copy(a, a + number, temp);
   delete [] a;                             // deallocate old memory
   a = temp;
}

template<class T>
class maxHeap
{
public:
    maxHeap(int initialCapacity = 10);
    ~maxHeap() {delete [] heap;}
    bool empty() const {return heapSize == 0;}
    int size() const
        {return heapSize;}
    const T& top()
       {// return max element
          if (heapSize == 0)
             exit(1);
          return heap[1];
       }
    void pop();
    void push(const T&);
    void initialize(T *, int);
    void deactivateArray()
       {heap = NULL; arrayLength = heapSize = 0;}
    void output(ostream& out) const;
private:
    int heapSize;       // number of elements in queue
    int arrayLength;    // queue capacity + 1
    T *heap;            // element array
};

template<class T>
maxHeap::maxHeap(int initialCapacity)
{// Constructor.
   if (initialCapacity < 1)
   {
       cout << "Initial capacity = " << initialCapacity << " Must be > 0";
       exit(1);
   }
   arrayLength = initialCapacity + 1;
   heap = new T[arrayLength];
   heapSize = 0;
}

template<class T>
void maxHeap::push(const T& theElement)
{// Add theElement to heap.

   // increase array length if necessary
   if (heapSize == arrayLength - 1)
   {// double array length
      changeLength1D(heap, arrayLength, 2 * arrayLength);
      arrayLength *= 2;
   }

   // find place for theElement
   // currentNode starts at new leaf and moves up tree
   int currentNode = ++heapSize;
   while (currentNode != 1 && heap[currentNode / 2] < theElement)
   {
      // cannot put theElement in heap[currentNode]
      heap[currentNode] = heap[currentNode / 2]; // move element down
      currentNode /= 2;                          // move to parent
   }

   heap[currentNode] = theElement;
}

template<class T>
void maxHeap::pop()
{// Remove max element.
   // if heap is empty return null
   if (heapSize == 0)   // heap empty
   {
       cout << "heap is empty!" << endl;
       exit(1);
   }

   // Delete max element
   heap[1].~T();

   // Remove last element and reheapify
   T lastElement = heap[heapSize--];

   // find place for lastElement starting at root
   int currentNode = 1,
       child = 2;     // child of currentNode
   while (child <= heapSize)
   {
      // heap[child] should be larger child of currentNode
      if (child < heapSize && heap[child] < heap[child + 1])
         child++;

      // can we put lastElement in heap[currentNode]?
      if (lastElement >= heap[child])
         break;   // yes

      // no
      heap[currentNode] = heap[child]; // move child up
      currentNode = child;             // move down a level
      child *= 2;
   }
   heap[currentNode] = lastElement;
}

#endif