Tensorflow入门(6)——多元线性回归
一、波士顿房价预测
波士顿房价数据集包括
506
个样本,每个样本包括
12个特征变量
和该地区的
平均房价
房价(单价)显然和多个特征变量相关,不是单变量线性回归(
一元线性回归
)问题选择多个特征变量来建立线性方程,这就是多变量线性回归(
多元线性回归
)问题
本数据集包含与波士顿房价相关的多个因素:
CRIM :城镇人均犯罪率
ZN :住宅用地超过25000 sq.ft. 的比例
INDUS : 城镇非零售商用土地的比例
CHAS :Charles河空变量(如果边界是河流,则为1;否则,为0)
NOX :一氧化氮浓度
RM :住宅平均房间数
AGE :1940年之前建成的自用房屋比例
DIS :到波士顿5个中心区域的加权距离
RAD :辐射性公路的靠近指数
TAX :每1万美元的全值财产税率
PTRATIO :城镇师生比例
LSTAT :人口中地位低下者的比例
MEDV :自住房的平均房价,单位:千美元
CRIM :城镇人均犯罪率
ZN :住宅用地超过25000 sq.ft. 的比例
INDUS : 城镇非零售商用土地的比例
CHAS :Charles河空变量(如果边界是河流,则为1;否则,为0)
NOX :一氧化氮浓度
RM :住宅平均房间数
AGE :1940年之前建成的自用房屋比例
DIS :到波士顿5个中心区域的加权距离
RAD :辐射性公路的靠近指数
TAX :每1万美元的全值财产税率
PTRATIO :城镇师生比例
LSTAT :人口中地位低下者的比例
MEDV :自住房的平均房价,单位:千美元
数据集以CSV格式存储,可通过Pandas库读取并进行格式转换
%matplotlib inline
import matplotlib.pyplot as plt
import tensorflow as tf
import tensorflow.contrib.learn as skflow
from sklearn.utils import shuffle
import numpy as np
import pandas as pd
# 通过Pandas导入数据
df = pd.read_csv("boston.csv", header=0)
print (df.describe())
# 载入本示例所需数据
df = np.array(df)
for i in range(12):
df[:,i] = (df[:,i]-df[:,i].min())/(df[:,i].max()-df[:,i].min())
#x_data = df[['CRIM', 'DIS', 'LSTAT']].values.astype(float) #选取其中3个比较重要的影响因素
x_data = df[:,:12]
#y_data = df['MEDV'].values.astype(float) #获取y
y_data = df[:,12]
# 定义占位符
x = tf.placeholder(tf.float32, [None,12], name = "x") # 3个影响因素
y = tf.placeholder(tf.float32, [None,1], name = "y")
# 创建变量
with tf.name_scope("Model"):
w = tf.Variable(tf.random_normal([12,1], stddev=0.01), name="w0")
b = tf.Variable(1., name="b0")
def model(x, w, b):
return tf.matmul(x, w) + b
pred= model(x, w, b)可以看到 b0 和 w0 都在命名空间 Model 下
命名空间name_scope
Tensorflow中常有数以千计节点,在可视化过程中很难一下子全部展示出来,因此可用name_scope为变量划分范围,在可视化中,这表示在计算图中的一个层级。
- name_scope 不会影响 用get_variable()创建的变量的名字
- name_scope 会影响 用Variable()创建的变量以及op_name
二、训练模型
# 训练模型
# 设置训练参数
train_epochs = 50 # 迭代次数
learning_rate = 0.01 #学习率
# 定义均方差损失函数
with tf.name_scope("LossFunction"):
loss_function = tf.reduce_mean(tf.pow(y-pred, 2)) #均方误差MSE
# 选择优化器
optimizer = tf.train.AdamOptimizer(learning_rate).minimize(loss_function)
# 声明会话
sess = tf.Session()
init = tf.global_variables_initializer()
# 生成图协议文件
logdir='D:/Project/Python/Tensorflow/log/boston'
tf.train.write_graph(sess.graph, logdir,'graph.pbtxt')
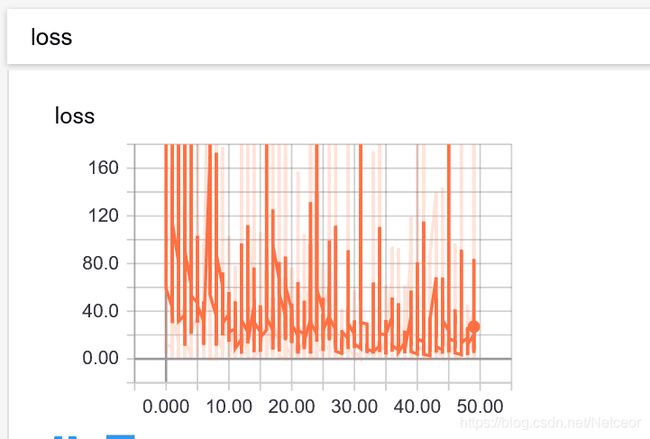
loss_op = tf.summary.scalar("loss", loss_function)
merged = tf.summary.merge_all()
sess.run(init)
# 创建摘要的文件写入符(FileWriter)
writer = tf.summary.FileWriter(logdir, sess.graph) 关于如何查看自己存储的图协议文件,可以参考Tensorflow入门(3)——TensorBoard可视化,已生成graph
# 迭代训练
loss_list = []
step=100
loss_list=[] #用于保存loss的列表,之后显示loss
for epoch in range (train_epochs):
loss_sum=0.0
for xs, ys in zip(x_data, y_data):
z1 = xs.reshape(1,12)
z2 = ys.reshape(1,1)
_,loss = sess.run([optimizer,loss_function], feed_dict={x: z1, y: z2})
# display_step:控制报告的粒度,即每训练几次输出一次损失值
# 与超参数不同,修改display_step不会改变模型所学习的规律
loss_list.append(loss)
step=step+1
display_step=10
if step%display_step==0:
print("Train Epoch:",'%02d'% (epoch+1),"Step:%03d"%(step),"loss=",\
"{:.9f}".format(loss))
summary_str = sess.run(loss_op, feed_dict={x: z1, y: z2})
#lossv+=sess.run(loss_function, feed_dict={x: z1, y: z2})/506.00
loss_sum = loss_sum + loss
# loss_list.append(loss)
writer.add_summary(summary_str, epoch)
x_data, y_data = shuffle(x_data, y_data)
print (loss_sum)
b0temp=b.eval(session=sess)
w0temp=w.eval(session=sess)
loss_average = loss_sum/len(y_data)
loss_list.append(loss_average)
print("epoch=", epoch+1,"loss=",loss_average,"b=", b0temp,"w=", w0temp )
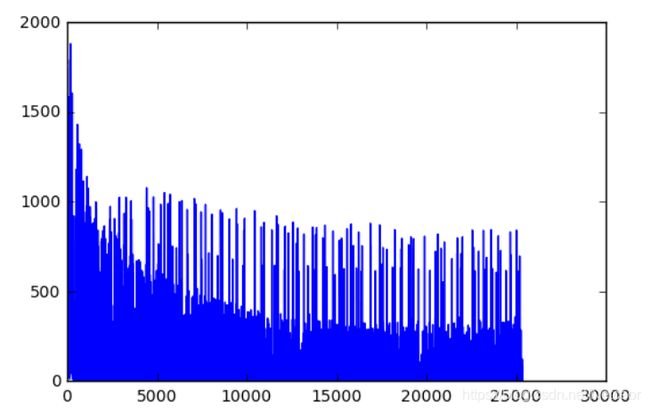
# 损失值可视化
print("y=",w0temp[0], "x1+",w0temp[1], "x2+",w0temp[2], "x3+", [b0temp])
print("y=",w0temp[0], "CRIM+", w0temp[1], 'DIS+', w0temp[2], "LSTAT+", [b0temp])
plt.plot(loss_list)在Tensorboard中也显示了损失