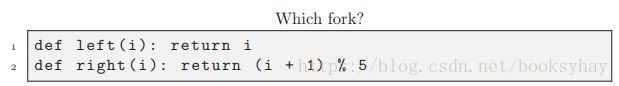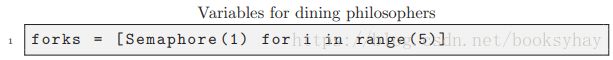The Little Book of Semaphores 信号量小书 第四章 经典同步问题 4.4 哲学家进餐
第四章 经典同步问题
4.4 哲学家进餐
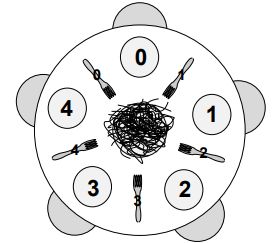
哲学家进餐问题是由Dijkstra在1965年提出的,当时恐龙统治了地球[3]。 它有许多个变种,但标准特征是一张桌子,上面有五个盘子,五个叉子(或筷子)和一大碗意大利面。 代表交互线程的五位哲学家来到桌前,并执行以下循环:
叉子表示线程必须保持的资源,以便取得进展。使问题变得有趣,不切实际和不卫生的事情是,哲学家需要两把叉子才能吃,所以一个饥饿的哲学家可能不得不等待邻居放下一把叉子。
假设哲学家有一个局部变量i,用于识别每个哲学家。它的值为(0..4)。 类似地,叉子从0到4编号,因此在哲学家i的右边有叉子i,在其左边有叉子i + 1。 这是一个情况图:
假设哲学家们知道如何思考和吃饭,我们的工作就是编写一个版本的get_forks()和put_forks()函数,以满足以下约束条件:
- 同一时刻,只有一位哲学家可以拿到同一个叉子。
- 必须不能发生死锁。
- 哲学家一定不能在等待叉子时饿死。
- 必须允许一个以上的哲学家同时吃饭。
关于最后一个要求的一种说法是,解决方案应该高效,也就是说,它应该允许最大的并发量。
我们不会假设会吃多久、要想多久,除了一条:吃饭最终必须停下来。 否则,第三个约束是不可能的 - 如果哲学家永远保留其中一个叉子,没有什么能阻止邻居饿死。
为了让哲学家能够轻松地引用他们的叉子,我们可以使用left()和right()函数:
%运算符在到达5时回绕,因此(4 + 1)% 5 = 0。
由于我们必须强制执行对叉子的独占访问,因此很自然地要使用信号量列表,每个叉子都有一个。 最初,所有的叉子都可用。
对于不使用Python的读者来说,这种用于初始化列表的符号可能是不熟悉的。 range函数返回一个包含5个元素的列表; 对于此列表的每个元素,Python创建一个初始值为1的信号量,并将结果汇总到名为forks的列表中。
下面初步尝试写出get_fork和put_fork函数:
很明显,这个解决方案满足第一个约束条件,但可以肯定它不满足其他两个约束条件。否则,这将不是一个有趣的问题,你该去阅读第5章。
思考:哪里不对?
4.4.1 死锁-5#
问题是桌子是圆的。 结果,每个哲学家都可以拿起一个叉子,然后永远等待另一个叉子。 死锁!
思考:写一个解决这个问题的方法来防止死锁。
提示:避免死锁的一种方法是考虑使死锁成为可能的条件,然后改变其中一个条件。 在这种情况下,死锁相当脆弱 - 一个非常小的变化就可以打破它。
4.4.2 哲学家进餐问题提示-1#
如果一次只允许四个哲学家在桌子上,那么就不可能发生死锁。
首先,让自己相信这种说法是正确的,然后写代码来限制桌上哲学家的数量。
4.4.3 哲学家进餐问题方案-1#
如果桌子上只有四位哲学家,那么在最坏的情况下,每个人都会拿起一把叉子。 即使这样,桌子上还有一个叉子,那个叉子有两个邻居,每个邻居都拿着另一个叉子。 因此,这些邻居中的任何一个都可以拿起剩余的叉子吃。
我们可以用一个名为footman的Multiplex【译注:多路复用,参见第3章第5节】来控制桌上哲学家的数量,该footman初始化为4。然后解决方案如下所示:
除了避免死锁,这个解决方案还保证没有哲学家挨饿。 想象一下,你坐在桌旁,两个邻居都在吃饭。 你被阻止等待你的右叉。 最终你的右邻居会把它放下,因为不能一直吃下去。 因为你是唯一等待该叉子的线程,所以您必须在下一步获得它。 通过类似的论证,你不会饿死等待你左叉的那位。
因此,哲学家在桌上花费的时间是有限的。 这意味着只要footman具备属性4(参见第4.3节),那么进入房间的等待时间也是有限的。
这个解决方案表明,通过控制哲学家的数量,我们可以避免死锁。 另一种避免死锁的方法是改变哲学家拿取叉子的顺序。 在最初的非解决方案中,哲学家都是“右撇子”;也就是说,他们先拿起正确的叉子。 但是,如果哲学家0是左撇子,会发生什么?
思考:证明如果至少有一个左撇子和至少一个右撇子,那么死锁是不可能的。
提示:死锁只有在所有5位哲学家都拿着一个叉子并且永远等待另一个叉子时才会发生。 否则,他们中的一个可以获得叉子,吃饭和离开。
用反证法来证明。 首先,假设死锁是可能的。然后选择一个据推测已陷入死锁的哲学家。 如果她是一个左撇子,你可以证明哲学家都是左撇子,这是矛盾的。 同样,如果她是一个右撇子,你可以证明哲学家都是右撇子。无论哪种方式,你都会产生矛盾; 因此,死锁是不可能的。
4.4.4 哲学家进餐问题方案-2#
在哲学家进餐问题的不对称解决方案中,必须至少有一名左撇子和至少一名右撇子。 在那种情况下,死锁是不可能的。 之前的提示概述了证据。 下面是详述。
重复一遍,如果死锁是可能的,那么就发生在当所有5位哲学家都拿着一个叉子并等待另一个叉子时。 如果我们假设哲学家j是左撇子,那么她必须握住她的左叉并等待她的右叉。 因此,她的右边邻居,哲学家k,必须拿着他的左叉,等待他的右邻居; 换句话说,哲学家k必须是左撇子。 重复同样的论点,我们可以证明哲学家都是左派,这与最初至少有一个右派的说法相矛盾。 因此死锁是不可能的。
我们用于前一解决方案的相同论点也证明了这种解决方案不可能会出现饿死。
4.4.5 Tanenbaum的方案
以前的解决方案没有任何问题,但为了完整起见,让我们看一些替代方案。 其中最著名的是出现在Tanenbaum流行的操作系统教科书中[12]。 每个哲学家都有一个表明他是在思考、吃饭还是等着吃(“饥饿”)的状态变量,和一个表示他是否可以开始进食的信号量。 以下是变量:
state是一个包含5个初始值为“思考”的列表。 sem是一个包含5个信号量的列表,其初始值为0。以下是代码:
test函数检查第i位哲学家是否可以开始进食,如果他是饥饿状态并且他的邻居都没有进食,他就可以开始吃。 如果是这样,test函数就发出信号量i。
有两种方式可以让哲学家开始吃。 在第一种情况下,哲学家执行get_forks,找到可用的叉子,并立即执行。 在第二种情况下,其中一个邻居正在吃东西,而哲学家则在自己的信号量上阻塞。 最终,其中一个邻居将完成,此时它会对其两个邻居执行test。 两个测试都可能成功,在这种情况下,邻居可以同时运行。 两个测试的顺序无关紧要。
为了访问state或调用test,线程必须持有互斥锁mutex。 因此,检查和更新数组的操作是原子的。 由于哲学家只有在我们知道两种叉子都可用时才能继续进行,因此可以保证对叉子的独占访问。
可能没有死锁,因为被多个哲学家访问的唯一信号量是互斥量mutex,并且没有线程在持有互斥量时执行wait。
但同样,饿死是很棘手的。
思考:要么说服自己,Tanenbaum的方案可以防止饿死,要么找到一种重复的模式,允许某个线程在其它线程取得进展的同时发生饿死。
4.4.5 饥饿的Tanenbaums
不幸的是,这种解决方案不是没有饥饿的。 Gingras证明了有重复的模式允许线程永远等待,而其他线程来来往往[4]。
想象一下,我们正试图饿死哲学家0。最初,2和4在桌子上,1和3饿了。假设2站起来,1坐下,然后4站起来,3坐下。现在我们处于起始位置的镜像中。
如果3站起来,4坐下,然后1站起来,2坐下,我们回到我们开始的地方。我们可以无限期地重复这个周期,哲学家0会饿死。
因此,Tanenbaum的解决方案并不能满足所有要求。