优先队列式分支限界法解01背包
概念:
分支限界采用的是广搜。
优先队列采用的是队列里最优的出队。(这里采用最大堆来实现活结点优先队列,最大堆以活结点的界值作为优先级)
说明:
对于优先队列式分支限界法解01背包,实际上是广搜遍历生成树的过程。因为01背包。背包只有选和不选。所以该生成树是一个二叉树。假设规定左叉标1(代表选择该物品装入背包),右叉标0(代表不选择该物品装入背包)。给定示例输入:
背包容量c=10
物品个数n=5
物品重量w={2,2,6,5,4}
物品价格p={6,3,5,4,6}
步骤:
左子树的解的上界与父节点相同,不用计算。右子树的解的界值:较好的就算方法是将剩余物品依其单位重量价值排序,然后依次装入物品,直到装不下时,再装入该物品的一部分来装满背包。由此得到的价值是右子树中解的上界(尽管这不是一个可行解,但可以证明其价值是最优值的上界)。
1.排好序的情况:
物品重量w={2,2,4,6,5}
物品价格p={6,3,6,5,4}
2.一层一层的将活结点加入到活结点优先队列中:
说明:
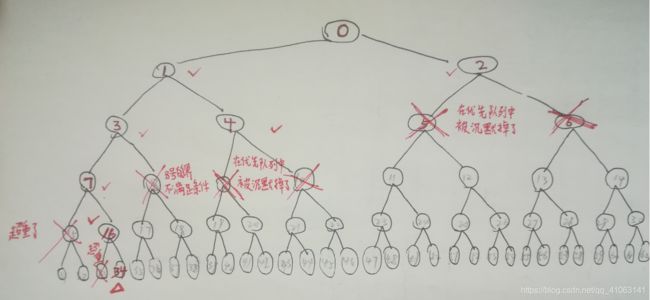
0.程序先是将1,2结点加入到队列中,由于1的界大于2的 界,所以选择1结点继续扩展(继续向下搜索)---进入到3,4结点的选择。由于父节点2没有出队。所以相继的5,6结点就被沉默掉了,故第二层只考虑3,4结点,3选择了2号物品后没有超重,4的界也大于当前背包的价格6+3=9.所以3,4都被加入到活结点,又由于3的界大于4的界,所以选择3作为扩展结点,继续向下进行扩展。。。。。。直到叶子结点。。。。程序结束
1.该生成树中:只要左儿子结点没超重就把他加入到活结点优先队列中来。只要右儿子结点的界值大于当前背包的价值,就将右儿子结点也加入到活结点优先队列中来。当进入到下一层的搜索时,会从上一层的活结点队列中选择最优的那个结点(界值最大的)作为父节点(扩展结点)进行扩展,向下搜索。而上一层没有机会出队的活结点将暂时被沉默掉,等待出队的机会
2.下面再附上MaxKanpsack()函数的运行数据变化图。方便更快速的理解代码。
注解:下图中:i=4, a'''=add(14>10),add其实是addlivenode()函数,这里的14表示当前结点下(选择1,2,3,4号物品后背包重量为14=2+2+4+6,明显大于了背包的重量10,所以a'''=add()也应该划叉,即该结点被终结了,因为超重了。下文的i=5,a'''=add(13>10)分析同上。)
各个节点界的计算:1结点:(6+3+6)+(10-2-2-4)*(5/6)=16.6666
2结点:(3+6)+(10-2-4)*(5/6)=12.3333 ...........................
8结点: (6+3)+(10-2-2)*(5/6)=14.00000
16结点: (6+3+6)+(10-2-2-4)*(4/5)=16.60000
34结点: (6+3+6)+(10-2-2-4)* 0=15
左儿子结点的界不用算,直接继承父节点的界(左儿子的界=父节点的界)3结点的界=1结点的界=7结点的界=16.66
过程说明:i=1时:第一层广搜:1和2结点作比较。由于1和2的界(16.6,12.3)都大于当前背包的价值6,故都加入活结点的优先队列中。又1的 界大于2的界,选择1作扩展结点(父节点)进入下一层。............
i=3时,背包价格:15=6+3+6;而8号的界为14<15(8号界小于当前背包重量,不加入活结点优先队列中),15号结点对应的背包重量是2+2+4+6=14>10(背包重量),超重了。
代码如下:
#include
#include
using namespace std;
typedef int Typew;
//typedef int Typep;
//物品类
class Object{
friend float Knapsack(Typew *, float *, Typew, int, int *);
public:
int operator <= (Object a) const{
return (d >= a.d);
}
private:
int ID; //物品编号
float d; //单位重量价值
};
//树结点类
class bbnode{
friend class Knap;
friend float Knapsack(Typew *, float *, Typew, int, int *);
private:
bbnode *parent; //指向父节点的指针
int LChild; //如果是左儿子结点取1,也即说明该物品已装进背包
};
//堆结点类
class HeapNode{
friend class Knap;
friend class MaxHeap;
public:
operator float()const{return uprofit;};
private:
float uprofit, //结点的价值上界
profit; //结点所相应的价值
Typew weight; //结点所相应的重量
int level; //活结点在子集树中所处的层序号
bbnode *elemPtr; //指向该活结点在子集树中相应结点的指针
};
//最大堆类
class MaxHeap{
public:
MaxHeap(int maxElem)
{
HeapElem = new HeapNode* [maxElem+1]; //下标为0的保留
capacity = maxElem;
size = 0;
}
void InsertMax(HeapNode *newNode);
HeapNode DeleteMax(HeapNode* &N);
private:
int capacity;
int size;
HeapNode **HeapElem;
};
//0-1背包问题的主类
class Knap{
//Knapsack主函数功能:解决初始化、求解最优值和最优解、回收内存
friend float Knapsack(Typew *, float *, Typew, int, int *);
public:
float MaxKnapsack();
private:
MaxHeap *H;
//Bound辅助Maxknapsack函数:计算结点价值上界
float Bound(int i);
//AddLiveNode辅助Maxknapsack函数:将活结点插入子集树和优先队列中
void AddLiveNode(float up, float cp, Typew cw, int ch, int level);
bbnode *E; //指向扩展结点的指针
Typew c; //背包容量
int n; //物品总数
Typew *w; //物品重量数组(以单位重量价值降序)
float *p; //物品价值数组(以单位重量价值降序)
Typew cw; //当前装包重量
float cp; //当前装包价值
int *bestx; //最优解
};
//这是博客上大牛自己写的,原教材上没有
void MaxHeap::InsertMax(HeapNode *newNode)
{
//极端情况下暂未考虑,比如堆容量已满等等
int i = 1;
for (i = ++size; i/2 > 0 && HeapElem[i/2]->uprofit < newNode->uprofit; i /= 2)
{
HeapElem[i] = HeapElem[i/2];
}
HeapElem[i] = newNode;
}
//这是博客上大牛自己写的,原教材上没有
HeapNode MaxHeap::DeleteMax(HeapNode *&N)
{
//极端情况下暂未考虑
if(size >0 )
{
N = HeapElem[1];
//从堆顶开始调整
int i = 1;
while(i < size)
{
if(((i*2 +1) <= size) && HeapElem[i*2]->uprofit > HeapElem[i*2 +1]->uprofit)
{
HeapElem[i] = HeapElem[i*2];
i = i*2;
}
else
{
if(i*2 <= size)
{
HeapElem[i] = HeapElem[i*2];
i = i*2;
}
else
break;
}
}
if(i < size)
HeapElem[i] = HeapElem[size];
}
size--;
return *N;
}
float Knap::MaxKnapsack()
{
H = new MaxHeap(1000);
bestx = new int [n+1];
//初始化,为处理子集树中的第一层做准备,物品i处于子集树中的第i层
int i = 1; //生成子集树中的第一层的结点
E = 0; //将首个扩展点设置为null,也就是物品1的父节点
cw = 0;
cp = 0;
float bestp = 0; //当前最优值
float up = Bound(1); // 选取物品1之后的价值上界
//当选择左儿子结点时,上界约束up不用关心,重量约束wt需要考虑。因为上界约束跟父节点相同。
//当选择右儿子结点时,上界约束up需要考虑,重量约束不需要考虑。因为父节点和该结点重量相同。
while (i != n+1)
{
//检查当前扩展结点的左儿子结点
int wi=w[i];
int pi=p[i];
int cp1=cp;
int cw1=cw;
int test=cw1+cp1;
Typew wt = cw + w[i]; //当前选择物品i之后的总重量wt
if(wt <= c) //背包能将物品i装下,也即当前扩展结点的左儿子结点可行
{
if(cp + p[i] > bestp)
bestp = cp +pi;
//bestp = cp + p[i]
AddLiveNode(up, cp + p[i], cw + w[i], 1, i);
}
//检查当前扩展结点的右儿子结点
up = Bound(i + 1); //未选择物品i之后的价值上界
if(up >= bestp)
AddLiveNode(up, cp, cw, 0, i);
//从优先队列中选择价值上界最大的结点成为扩展结点
HeapNode* N;
H->DeleteMax(N);
E = N->elemPtr;
cw = N->weight;
cp = N->profit;
up = N->uprofit;
i = N->level + 1; //准备生成N.level+1层的子集树结点
}
//从子集树中的某叶子结点开始构造当前最优解
for (int i = n; i > 0; i--)
{
bestx[i] = E->LChild;
E = E->parent;
}
return cp;
}
float Knap::Bound(int i)
{
Typew cleft = c - cw;
float b = cp;
while (i<=n && w[i] <= cleft)
{
cleft -= w[i];
b += p[i];
i++;
}
if(i<=n) b += p[i]/w[i] * cleft;
return b;
}
void Knap::AddLiveNode(float up, float cp, Typew cw, int ch, int level)
{
bbnode *b=new bbnode;
b->parent=E;
b->LChild=ch;
HeapNode *N = new HeapNode;
N->uprofit=up;
N->profit=cp;
N->weight=cw;
N->level=level;
N->elemPtr=b;
H->InsertMax(N);
}
//Knapsack返回最大价值,最优值保存在bestx
float Knapsack(Typew *w, float *p, Typew c, int n, int *bestx)
{//数组w、p和bestx中下标为0的元素保留不用
//初始化
Typew W = 0;
float P = 0;
Object *Q = new Object[n];
for(int i =1; i<=n; i++)
{
Q[i-1].ID = i;
Q[i-1].d = 1.0*p[i]/w[i];
P += p[i];
W += w[i];
}
//所有物品的总重量小于等于背包容量c
if (W <= c)
{
for(int i =1; i<=n; i++)
{
bestx[i] = p[i];
}
return P;
}
//所有物品的总重量大于背包容量c,存在最佳装包方案
//sort(Q,n);对物品以单位重量价值降序排序
//1.对物品以单位重量价值降序排序
//采用简单冒泡排序
for(int i = 1; i 上述代码对于w={3,4,5} p={4,5,6} c=6 执行的结果有误
再附上修正后的:
#ifndef BEIBAO_H
#define BEIBAO_H
#include
#include
using namespace std;
//子空间中节点类型
class BBnode{
public:
BBnode* parent; //父节点
bool leftChild; //左儿子节点标志
BBnode(BBnode* par,bool ch){
parent=par;
leftChild=ch;
}
BBnode(){
}
};
class HeapNode {
public:
BBnode* liveNode; // 活结点
double upperProfit; //结点的价值上界
double profit; //结点所相应的价值
double weight; //结点所相应的重量
int level; // 活结点在子集树中所处的层次号
//构造方法
HeapNode(BBnode* node, double up, double pp , double ww,int lev){
liveNode = node;
upperProfit = up;
profit = pp;
weight = ww;
level = lev;
}
HeapNode(){
}
int compareTo(HeapNode o) {
double xup =o.upperProfit;
if(upperProfit < xup)
return -1;
if(upperProfit == xup)
return 0;
else
return 1;
}
};
class Element {
public:
int id;
double d;
Element(){
}
Element(int idd,double dd){
id=idd;
d=dd;
}
int compareTo(Element x){
double xd=x.d;
if(d0;--i){
heapAdjust(nodes,i,nextPlace-1);
}
}
} ;
#endif
//子空间中节点类型
double c=10;
const int n=5;
double *w;
double *p;
double cw;
double cp;
int *bestX;
MaxHeap * heap;
//上界函数bound计算结点所相应价值的上界
double bound(int i){
double cleft=c-cw;
double b=cp;
while(i<=n&&w[i]<=cleft){
cleft=cleft-w[i];
b=b+p[i];
i++;
}
//装填剩余容量装满背包
if(i<=n)
b=b+p[i]/w[i]*cleft;
return b;
}
//addLiveNode将一个新的活结点插入到子集树和优先队列中
void addLiveNode(double up,double pp,double ww,int lev,BBnode* par,bool ch){
//将一个新的活结点插入到子集树和最大堆中
BBnode *b=new BBnode(par,ch);
HeapNode node =HeapNode(b,up,pp,ww,lev);
heap->put(node);
}
double MaxKnapsack(){
//优先队列式分支限界法,返回最大价值,bestx返回最优解
BBnode * enode=new BBnode();
int i=1;
double bestp=0;//当前最优值
double up=bound(1);//当前上界
while(i!=n+1){//非叶子结点
//检查当前扩展结点的左儿子子结点
double wt=cw+w[i];
if(wt<=c){
if(cp+p[i]>bestp)
bestp=cp+p[i];
addLiveNode(up,cp+p[i],cw+w[i],i+1,enode,true);
}
up=bound(i+1);
if(up>=bestp)
addLiveNode(up,cp,cw,i+1,enode,false);
HeapNode node =heap->removeMax();
enode=node.liveNode;
cw=node.weight;
cp=node.profit;
up=node.upperProfit;
i=node.level;
}
for(int j=n;j>0;j--){
bestX[j]=(enode->leftChild)?1:0;
enode=enode->parent;
}
return cp;
}
double knapsack(double *pp,double *ww,double cc,int *xx){
//返回最大值,bestX返回最优解
c=cc;
//n=sizeof(pp)/sizeof(double);
//定义以单位重量价值排序的物品数组
Element *q=new Element[n];
double ws=0.0;
double ps=0.0;
for(int i=0;i 图片: