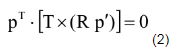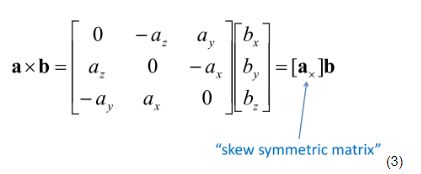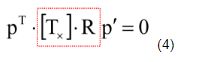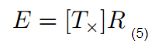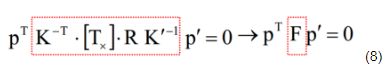计算机视觉——基础矩阵原理
基础矩阵(Fundamental Matrix)
如果已知基础矩阵F,以及一个3D点在一个像面上的像素坐标p,则可以求得在另一个像面上的像素坐标p‘。这个是基础矩阵的作用,可以表征两个相机的相对位置及相机内参数。
下面具体介绍基础矩阵与像素坐标p和p’的关系。
以O1为原点,光轴方向为z轴,另外两个方向为x,y轴可以得到一个坐标系,在这个坐标系下,可以对P,p1(即图中所标p),p2(即图中所标p‘)得到三维坐标,同理,对O2也可以得到一个三维坐标,这两个坐标之间的转换矩阵为[RT],即通过旋转R和平移T可以将O1坐标系下的点P1(x1,y1,z1),转换成O2坐标系下的P2(x2,y2,z2)。
则可知,P2=R(P1-T)(1)
采用简单的立体几何知识,可以知道
其中,p,p‘分别为P点的像点在两个坐标系下分别得到的坐标(非二维像素坐标)。Rp’为极面上一矢量,T为极面上一矢量,则两矢量一叉乘为极面的法向量,这个法向量与极面上一矢量p一定是垂直的,所以上式一定成立。(这里采用转置是因为p会表示为列向量的形式,此处需要为行向量)
采用一个常用的叉乘转矩阵的方法,
将我们的叉乘采用上面的转换,会变成
红框中所标即为本征矩阵E,他描述了三维像点p和p‘之间的关系
有了本征矩阵,我们的基础矩阵也就容易推导了
注意到将p和p‘换成P1和P2式(4)也是成立的,且有
q1=K1P1(6)
q2=K2P2(7)
上式中,K1K2为相机的校准矩阵,描述相机的内参数q1q2为相机的像素坐标代入式(4)中,得
上式中p->q1,p‘->q2
这样我们就得到了两个相机上的像素坐标和基础矩阵F之间的关系了
代码:
# coding: utf-8
# In[1]:
from PIL import Image
from numpy import *
from pylab import *
import numpy as np
# In[2]:
from PCV.geometry import camera
from PCV.geometry import homography
from PCV.geometry import sfm
from PCV.localdescriptors import sift
from PCV.geometry import camera
from PCV.geometry import homography
from PCV.geometry import sfm
from PCV.localdescriptors import sift
from imp import reload
camera = reload(camera)
homography = reload(homography)
sfm = reload(sfm)
sift = reload(sift)
# In[3]:
# Read features
im1 = array(Image.open('1.jpg'))
sift.process_image('1.jpg', 'im1.sift')
im2 = array(Image.open('2.jpg'))
sift.process_image('2.jpg', 'im2.sift')
# In[4]:
l1, d1 = sift.read_features_from_file('im1.sift')
l2, d2 = sift.read_features_from_file('im2.sift')
# In[5]:
matches = sift.match_twosided(d1, d2)
# In[6]:
ndx = matches.nonzero()[0]
x1 = homography.make_homog(l1[ndx, :2].T)
ndx2 = [int(matches[i]) for i in ndx]
x2 = homography.make_homog(l2[ndx2, :2].T)
d1n = d1[ndx]
d2n = d2[ndx2]
x1n = x1.copy()
x2n = x2.copy()
# In[7]:
figure(figsize=(16,16))
sift.plot_matches(im1, im2, l1, l2, matches, True)
show()
# In[26]:
#def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6):
def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6):
""" Robust estimation of a fundamental matrix F from point
correspondences using RANSAC (ransac.py from
http://www.scipy.org/Cookbook/RANSAC).
input: x1, x2 (3*n arrays) points in hom. coordinates. """
from PCV.tools import ransac
data = np.vstack((x1, x2))
d = 10 # 20 is the original
# compute F and return with inlier index
F, ransac_data = ransac.ransac(data.T, model,
8, maxiter, match_threshold, d, return_all=True)
return F, ransac_data['inliers']
# In[27]:
# find F through RANSAC
model = sfm.RansacModel()
F, inliers = F_from_ransac(x1n, x2n, model, maxiter=5000, match_threshold=1e-5)
print(F)
# In[28]:
P1 = array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0]])
P2 = sfm.compute_P_from_fundamental(F)
# In[29]:
print (P2)
print (F)
# In[30]:
# P2, F (1e-4, d=20)
# [[ -1.48067422e+00 1.14802177e+01 5.62878044e+02 4.74418238e+03]
# [ 1.24802182e+01 -9.67640761e+01 -4.74418113e+03 5.62856097e+02]
# [ 2.16588305e-02 3.69220292e-03 -1.04831621e+02 1.00000000e+00]]
# [[ -1.14890281e-07 4.55171451e-06 -2.63063628e-03]
# [ -1.26569570e-06 6.28095242e-07 2.03963649e-02]
# [ 1.25746499e-03 -2.19476910e-02 1.00000000e+00]]
# In[31]:
# triangulate inliers and remove points not in front of both cameras
X = sfm.triangulate(x1n[:, inliers], x2n[:, inliers], P1, P2)
# In[32]:
# plot the projection of X
cam1 = camera.Camera(P1)
cam2 = camera.Camera(P2)
x1p = cam1.project(X)
x2p = cam2.project(X)
# In[33]:
figure(figsize=(16, 16))
imj = sift.appendimages(im1, im2)
imj = vstack((imj, imj))
imshow(imj)
cols1 = im1.shape[1]
rows1 = im1.shape[0]
for i in range(len(x1p[0])):
if (0<= x1p[0][i]实现结果:
室外图像对比(一张近图,一张远拍)
基础矩阵F
相机矩阵:(投影矩阵)
sift特征匹配
室内图像比对:
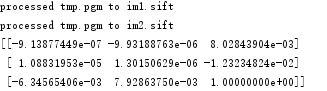
基础矩阵:
相机矩阵(投影矩阵):