用线性回归对波士顿房价预测

from __future__ import print_function
from sklearn import datasets   #导入自带的数据库
from sklearn.linear_model import LinearRegression    #从线性模型中导入模块
import matplotlib.pyplot as plt

建立线性模型

loaded_data = datasets.load_boston()#从自带数据库中下载波士顿房价数据
data_X = loaded_data.data#加载房屋属性参数
data_y = loaded_data.target#加载房屋均价

model = LinearRegression()#线性回归模型

model.fit(data_X, data_y)#用模型拟合两个标签

print(model.predict(data_X[:4, :]))

[30.00384338 25.02556238 30.56759672 28.60703649]

输出可对数据集进行哪些操作

print(loaded_data.keys())

dict_keys([‘data’, ‘target’, ‘feature_names’, ‘DESCR’, ‘filename’])，即说明可用这些方法（数据、目标值、列标签、描述性统计、文件地址）查看数据集

loaded_data.feature_names #输出每一列的标签

array([‘CRIM’, ‘ZN’, ‘INDUS’, ‘CHAS’, ‘NOX’, ‘RM’, ‘AGE’, ‘DIS’, ‘RAD’,
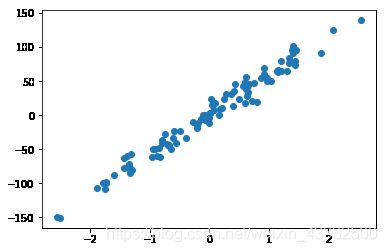
‘TAX’, ‘PTRATIO’, ‘B’, ‘LSTAT’], dtype=’

绘图

X, y = datasets.make_regression(n_samples=100, n_features=1, n_targets=1, noise=10)
plt.scatter(X, y)

模型结果

model.coef_#模型系数

array([-1.08011358e-01, 4.64204584e-02, 2.05586264e-02, 2.68673382e+00,
-1.77666112e+01, 3.80986521e+00, 6.92224640e-04, -1.47556685e+00,
3.06049479e-01, -1.23345939e-02, -9.52747232e-01, 9.31168327e-03,
-5.24758378e-01])

model.intercept_ #输出模型的截距（与y轴的交点）

36.459488385089855

model.score(data_X, data_y) #对 Model 用 R^2 的方式进行打分

0.7406426641094095

训练模型

划分测试集和训练集： X_train,X_test, y_train, y_test =train_test_split(train_data,train_target,test_size=0.3, random_state=0)
参数解释：

train_data：被划分的样本特征集
train_target：被划分的样本标签
test_size：如果是浮点数，在0-1之间，表示样本占比；如果是整数的话就是样本的数量
random_state：是随机数的种子。
随机数种子：其实就是该组随机数的编号，在需要重复试验的时候，保证得到一组一样的随机数。比如你每次都填1，其他参数一样的情况下你得到的随机数组是一样的。但填0或不填，每次都会不一样。

from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(data_X,data_y,test_size=0.2)#划分测试集和训练

StandardScaler是数据放缩的其中一种方案，即f(x)=(x-平均值)/标准差

scaler = preprocessing.StandardScaler(copy=True, with_mean=True, with_std=True)

数据标准化处理：sklearn.preprocessing.scale(X, axis=0, with_mean=True,with_std=True,copy=True)

参数解释：
X：数组或者矩阵
axis：int类型，初始值为0，axis用来计算均值 means 和标准方差 standard deviations. 如果是0，则单独的标准化每个特征（列），如果是1，则标准化每个观测样本（行）。
with_mean: boolean类型，默认为True，表示将数据均值规范到0
with_std: boolean类型，默认为True，表示将数据方差规范到1

scaler.fit(x_train)
x_train = scaler.transform(x_train)
x_test = scaler.transform(x_test)

在数据模型建立时，只能使用训练组数据，因此使用训练组数据的标准差进行标准化；再分别对训练组和测试组数据进行标准化

from sklearn.svm import SVR
from numpy import *

svr = SVR(kernel='rbf')    #构建基于rbf（径向基函数）的SVR模型
svr.fit(x_train,y_train)    #将训练组数据输入进行训练
y_predict = svr.predict(x_test)   #将处理过的预测组数据输入进行预测，得出结果
#将实际结果与预测结果对比观察，2列的数组，左边列是实际结果，右边列是预测结果
result = hstack((y_test.reshape(-1,1),y_predict.reshape(-1,1)))
print(result)

部分结果

[[ 8.8        19.92420923]
 [22.1        24.06498602]
 [18.2        18.33370706]
 [43.1        32.87796988]
 [17.8        20.07679863]
 [50.         33.2143534 ]
 [19.3        20.21976937]
 [15.2        17.00127057]
 [34.9        27.67568313]
 [14.3        16.01604778]
 [22.9        21.60096462]
 [18.7        18.75527138]
 [12.5        15.55420713]
 [20.7        22.42926632]
 [36.2        24.23288538]
 [28.5        29.161016  ]
 [23.4        22.25782883]