张正友相机标定法的原理详述+标定相机参数的实现(Python+OpenCV)

原理详解

张正友于1998年在论文："A Flexible New Technique fro Camera Calibration"提出了基于单平面棋盘格的相机标定方法。该方法介于传统的标定方法和自标定方法之间，使用简单实用性强，有以下优点：

1. 不需要额外的器材，一张打印的棋盘格即可。
2. 标定简单，相机和标定板可以任意放置。
3. 标定的精度高。

相机的内参数

设 $P=(X,Y,Z)$ 为场景中的一点，进行下面几个步骤：

1. 将 $P$ 从世界坐标系通过刚体变换变换到相机坐标系，这个变换过程使用的是相机间的相对位姿，也就是相机的外参数。
2. 从相机坐标系，通过透视投影变换到相机的成像平面上的像点p=(x,y)。
3. 将像点p从成像坐标系，通过缩放和平移变换到像素坐标系上点p=(μ,ν)。

我们就可以将场景中的三维点转换成图像中的二维点了。上述的变换步骤转换成具体的数学形式：$$\begin{gathered} s\left(\begin{array}{c}\mu \\ \nu \\ 1\end{array}\right)=\left[\begin{array}{ccc}\alpha & 0& c_x\\ 0& \beta & c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{cc}R& t\\ 0^T& 1\end{array}\right]\left(\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right) \\ =\left[\begin{array}{cccc}{f}_x& 0& c_x& 0\\ 0& f_y& c_y& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{cc}R& t\\ 0^T& 1\end{array}\right]\left(\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right) \end{gathered}$$
将矩阵$K$称为相机的内参数,
$$K=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]$$

单应矩阵

在张氏标定法中，用于标定的棋盘格是三维场景中的一个平面 $\Pi$ ；其在成像平面的像是另一个平面 $\pi$ ，由于棋盘格的角点是已知的，我们可以通过角点提取算法获得图像中的角点，知道了两个平面的对应点的坐标，就可以求解得到两个平面的单应矩阵$H$。
通过上面的相机模型有：
$$p=K[R|t]P$$
其中p是像点坐标，P是标定的棋盘坐标。 这样就可以得到下面的等式：
$$H=K[R|t]$$
$H$ 表示的是成像平面和标定棋盘平面之间的单应矩阵。通过对应的点对解得H后，则可以通过上面的等式得到相机的内参数 $K$，以及外参旋转矩阵$R$和平移向量 $t$。
将一个平面映射到另一个平面，将棋盘格所在的平面映射到相机的成像平面，可以获得公式：
$$p=HP$$
其中$p$ 为棋盘格所成像的像点坐标，$P$ 棋盘格角点在世界坐标系的坐标。
设棋盘格所在的平面为世界坐标系中$Z=0$的平面，则根据相机模型：
$$s\left(\begin{array}{c}u\\ v\\ 1\end{array}\right)=K\left[\begin{array}{cc}R& t\end{array}\right]\left(\begin{array}{c}X\\ Y\\ 0\\ 1\end{array}\right)=K[\begin{array}{cccc}{r}_1& r_2& r_3& t\end{array}]\left(\begin{array}{c}X\\ Y\\ 0\\ 1\end{array}\right)=K[\begin{array}{ccc}{r}_1& r_2& t\end{array}]\left(\begin{array}{c}X\\ Y\\ 1\end{array}\right)$$
根据单应性，将公式进行整合，可以得到单应矩阵H和相机矩阵（包含内参和外参）的相等：$$H=\lambda K[\begin{array}{ccc}{r}_1& r_2& t\end{array}]$$
这样就能通过单应矩阵$H$来约束相机的内参和外参，单应矩阵$H$可以通过棋盘平和成像平面上对应的点计算出来。

内参约束条件

通过平面间的单应，可以把H矩阵(3*3)写成3个列向量形式，我们把H矩阵写成：$$H=\left[\begin{array}{ccc}{h}_1& h_2& h_3\end{array}\right]=\lambda K[\begin{array}{ccc}{r}_1& r_2& t\end{array}]$$
r1和r2标准正交，结合上面可以获得两个内参的约束等式：
$$\{\begin{array}{l}{h}_1^T{K}^{-T}{K}^{-1}{h}_2=0\\ h_1^T{K}^{-T}{K}^{-1}{h}_1=h_2^T{K}^{-T}{K}^{-1}{h}_2=1\end{array}$$

求解内参数

通过一幅标定板的图像可以的得到关于内参数的两个等式，令$$B=K^{-T}{K}^{-1}=\left[\begin{array}{ccc}{B}_{11}& B_{12}& B_{13}\\ B_{21}& B_{22}& B_{23}\\ B_{31}& B_{32}& B_{33}\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{{\alpha }^2}& -\frac{\gamma }{{\alpha }^2\beta }& \frac{v_0\gamma -u_0\beta }{{\alpha }^2\beta }\\ -\frac{\gamma }{{\alpha }^2\beta }& \frac{{\gamma }^2}{{\alpha }^2{\beta }^2}+\frac{1}{{\beta }^2}& -\frac{\gamma (v_0\gamma -u_0\beta )}{{\alpha }^2{\beta }^2}-\frac{v_0}{{\beta }^2}\\ \frac{v_0\gamma -u_0\beta }{{\alpha }^2\beta }& -\frac{\gamma (v_0\gamma -u_0\beta )}{{\alpha }^2{\beta }^2}-\frac{v_0}{{\beta }^2}& \frac{(v_0\gamma -u_0\beta {)}^2}{{\alpha }^2{\beta }^2}+\frac{v_0}{{\beta }^2}+1\end{array}\right]$$
可知B矩阵是个对称矩阵，所以可以写成一个6维向量形式$$b=\left[\begin{array}{c}{B}_{11},B_{12},B_{22},B_{13},B_{23},B_{33}\end{array}\right]$$
我们把$H$矩阵的列向量形式为：$h_i=[h_{i1},h_{i2},h_{i3}{]}^T$
整合公式：$$\begin{gathered} h_i{K}^{-T}{K}^{-1}{h}_j=h_{i}B{h}_j=v_{ij}^{T}b \\ 其中，v_{ij}={\left[\begin{array}{cccccc}{h}_{i1}{h}_{j1}& h_{i1}{h}_{j2}+h_{i2}{h}_{j1}& h_{i2}{h}_{j2}& h_{i3}{h}_{j1}+h_{i1}{h}_{j3}& h_{i3}{h}_{j2}+h_{i2}{h}_{j3}& h_{i3}{h}_{j3}\end{array}\right]}^T \end{gathered}$$
再结合上面求出的内参的约束条件，可得到矩阵：$$\left[\begin{array}{c}{v}_{12}^T\\ v_{11}-v_{22}\end{array}\right]b=0$$
若有n幅图像，则$$Vb=0$$
其中，V是一个2n×6的矩阵，b是一个6维向量，所以:

当$n\ge 3$，可以得到b的唯一解;
当$n=2$，则可以假设扭曲参数γ=0作为额外的约束条件
当$n=1$，则值能计算两个相机的内参数
对于方程$Vb=0$可以使用SVD求得其最小二乘解。对$V^{T}V$进行SVD分解，其最小特征值对应的特征向量就是$Vb=0$的最小二乘解，从而求得矩阵B。
可以得到相机的各个内参数：
$$\{\begin{array}{l}{c}_x=\gamma c_y/\beta -B_{13}{\alpha }^2/\lambda \\ c_y=(B_{12}{B}_{13}-B_{11}{B}_{23})/(B_{11}{B}_{22}-B_{12}^2)\\ \alpha =\sqrt{\lambda /B_{11}}\\ \beta =\sqrt{\lambda B_{11}/(B_{11}{B}_{22}-B_{12}^2)}\\ \gamma =-B_{12}{\alpha }^2\beta /\lambda \\ \lambda =B_{33}-[B_{13}^2+c_y(B_{12}{B}_{13}-B_{11}{B}_{23})]/B_{11}\end{array}$$

最大似然估计

由于上面估计获得的解可能存在高斯噪声，所以使用最大似然估计进行优化。
假设同一相机从$n$个不同的角度的得到了$n$幅标定板的图像，每幅图像上有$m$个像点。$M_{ij}$表示第$i$幅图像上第$j$个像点对应的标定板上的三维点，则$$\hat{m}(K,R_i,t_i,M_{ij})=K[\begin{array}{cc}R& t\end{array}]M_{ij}$$
$\hat{m}(K,R_i,t_i,M_{ij})$表示$M_{ij}$的像点。其中，$R_i,t_i$表示第i幅图像对应相机的旋转矩阵和平移向量，K是相机的内参数。则像点$m_{ij}$的概率密度函数是$$f(m_{ij})=\frac{1}{\sqrt{2\pi }}{e}^{\frac{-(\hat{m}(K,R_i,t_i,M_{ij})-m_{ij}{)}^2}{{\sigma }^2}}$$

构造似然函数$$L(A,R_i,t_i,M_{ij})=\prod _{i=1,j=1}^{n,m}f(m_{ij})=\frac{1}{\sqrt{2\pi }}{e}^{\frac{-{\sum }_{i=1}^n{\sum }_{j=1}^m(\hat{m}(K,R_i,t_i,M_{ij})-m_{ij}{)}^2}{{\sigma }^2}}$$
让L取得最大值，即让下面式子最小$$\sum _{i=1}^n\sum _{j=1}^m\Vert \hat{m}(K,R_i,t_i,M_{ij})-m_{ij}{\Vert }^2$$

消除径向畸变

为了取得好的成像效果，通常要在相机的镜头前添加透镜。在相机成像的过程中，透镜会对光线的传播产生影响，从而影响相机的成像效果，产生畸变：

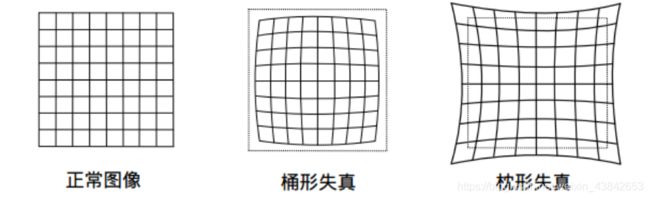
透镜自身的形状对才光线的传播产生影响，形成的畸变称为径向畸变。在小孔模型中，一条指向在成像平面上的像仍然是直线。但是在实际拍摄的过程中，由于透镜的存在，往往将一条直线投影成了曲线，越靠近图像的边缘，这种现象越明显。透镜往往是中心对称的，使得这种不规则的畸变通常是径向对称的。主要有两大类：桶形畸变和枕形畸变。

张氏标定法只关注了影响最大的径向畸变。则数学表达式为： $$\begin{gathered} \hat{u}=u+(u-u_0)[k_1(x^2+y^2)+k_2(x^2+y^2{)}^2] \\ \hat{v}=v+(v-v_0)[k_1(x^2+y^2)+k_2(x^2+y^2{)}^2]￥ \end{gathered}$$
其中，$(u,v)$是理想无畸变的像素坐标，$(\hat{u},\hat{v})$是实际畸变后的像素坐标。$(u0,v0)$代表主点，$(x,y)$是理想无畸变的连续图像坐标，$(\hat{x},\hat{y})$是实际畸变后的连续图像坐标。$k1$和$k2$为前两阶的畸变参数。
$$\begin{gathered} \hat{u}=u_0+\alpha \hat{x}+\gamma \hat{y} \\ \hat{v}=v_0+\beta \hat{y} \end{gathered}$$
化作矩阵形式：$$\left[\begin{array}{cc}(u-u_0)(x^2+y^2)& (u-u_0)(x^2+y^2{)}^2\\ (v-v_0)(x^2+y^2)& (v-v_0)(x^2+y^2{)}^2\end{array}\right]\left[\begin{array}{c}{k}_1\\ k_2\end{array}\right]=\left[\begin{array}{c}\hat{u}-u\\ \hat{v}-v\end{array}\right]$$
记作：$$Dk=d$$
则可得畸变系数：$$k=[k_1{k}_2{]}^T=(D^{T}D{)}^{-1}{D}^{T}d$$
使用最大似然的思想优化得到的结果，即像上一步一样，LM法计算下列函数值最小的参数值： $$\sum _{i=1}^n\sum _{j=1}^m\Vert \hat{m}(K,k_1,k_2,R_i,t_i,M_{ij})-m_{ij}{\Vert }^2$$

参考文献：https://blog.csdn.net/u010128736/article/details/52860364

openCV相机标定

实验步骤：

1. 先准备一张标定板（棋盘格）我用的是下图：

2. 拍摄棋盘格图片，10-20幅左右
3. 读取棋盘格图像，提取图像角点，使用findChessboardCorners函数提取角点，这里的角点专指的是标定板上的内角点，这些角点与标定板的边缘不接触。
4. 为了提高角点提取精度，使用cornerSubPix函数进行亚像素角点的提取
5. 在棋盘标定图上找到的内角点，使用drawChessboardCorners函数绘制被成功标定的角点。
   下图为其中一张角点标定图
   
6. 相机标定，使用calibrateCamera函数进行标定，计算相机内参和外参系数
7. 畸变矫正，用undistort函数矫正产生的畸变

标定结果（iPhone7）：

左图为原图，右图为畸变校正图。

参考文献：https://blog.csdn.net/dcrmg/article/details/52939318

另附代码：

import cv2
import numpy as np
import glob

# 设置寻找亚像素角点的参数，采用的停止准则是最大循环次数30和最大误差容限0.001
criteria = (cv2.TERM_CRITERIA_MAX_ITER | cv2.TERM_CRITERIA_EPS, 30, 0.001)

# 获取标定板角点的位置
objp = np.zeros((6 * 4, 3), np.float32)
objp[:, :2] = np.mgrid[0:6, 0:4].T.reshape(-1, 2)  # 将世界坐标系建在标定板上，所有点的Z坐标全部为0，所以只需要赋值x和y

obj_points = []  # 存储3D点
img_points = []  # 存储2D点

images = glob.glob("E:/PycharmProjects/xiangji/*.jpg")
for fname in images:
    img = cv2.imread(fname)
    cv2.imshow('img',img)
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

    size = gray.shape[::-1]
    ret, corners = cv2.findChessboardCorners(gray, (6, 4), None)
    print(ret)

    if ret:

        obj_points.append(objp)

        corners2 = cv2.cornerSubPix(gray, corners, (5, 5), (-1, -1), criteria)  # 在原角点的基础上寻找亚像素角点
        #print(corners2)
        if [corners2]:
            img_points.append(corners2)
        else:
            img_points.append(corners)

        cv2.drawChessboardCorners(img, (8, 6), corners, ret)  # 记住，OpenCV的绘制函数一般无返回值
        cv2.imshow('img', img)
        cv2.waitKey(10)

print(len(img_points))
cv2.destroyAllWindows()

# 标定
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points, size, None, None)

print("ret:", ret)
print("mtx:\n", mtx) # 内参数矩阵
print("dist:\n", dist)  # 畸变系数   distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print("rvecs:\n", rvecs)  # 旋转向量  # 外参数
print("tvecs:\n", tvecs ) # 平移向量  # 外参数

print("-----------------------------------------------------")
img = cv2.imread(images[2])
h, w = img.shape[:2]
newcameramtx, roi = cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),1,(w,h))#显示更大范围的图片（正常重映射之后会删掉一部分图像）
print (newcameramtx)
dst = cv2.undistort(img,mtx,dist,None,newcameramtx)
x,y,w,h = roi
dst1 = dst[y:y+h,x:x+w]
cv2.imwrite('calibresult3.jpg', dst1)
print ("dst的大小为:", dst1.shape)