深度学习优化方法：梯度下降法及其变形

优化与大家的日常生活息息相关。具体是指改变输入 x 以最小化或者最大化某个函数 f(x) 。如空调温度固定到多少时会使耗能最小、工厂需要多少机器才能效益最大……通常都以最小化 f(x) 指代大多数最优化问题，因为最大化可经由最小化算法优化 −f(x) 来实现。具体的描述如下所示：

x∗=argminf(x),x为实数.

如何确定较好的的最小化算法使得上述问题的求解高效准确？先假定函数的导数记为 f′(x) 或 ∂f(x)/∂x ，表示的是 f(x) 在点 x 处的斜率。直观的描述是导数表明如何缩放输入的小变化才能在输出获得相应的变化：

f(x+ϵ)≈f(x)+ϵf′(x).

因此发现导数对于函数最小化优化很有用，它可以直接告诉我们如何更改 x 来略微改善 y=f(x) 。例如在最小化问题中，我们知道对于足够小的 ϵ 来说， f(x−ϵsign(f′(x)) 是比 f(x) 小的。因此可以通过向导数的反方向移动一小步来减小 f(x) 。这种技术便被成为梯度下降（Gradient Descent）。梯度下降建议的新点为：

x2=x1−ϵf′(x1)={向右移动,向左移动,f′(x1)<0f′(x1)>0

其中 ϵ 是学习率，是一个确定步长大小的正标量，通常选择为一个大于0的小常量。

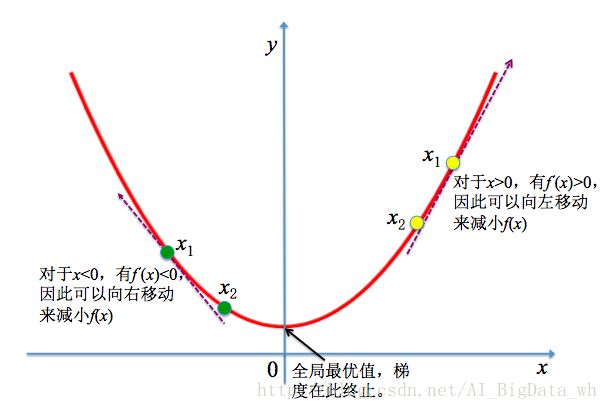
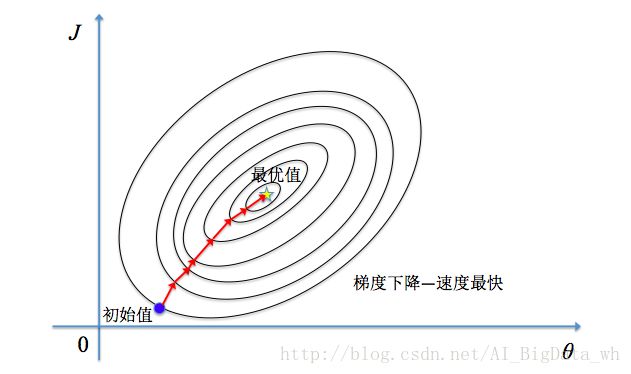
梯度下降法（Gradient descent）是求解无约束最优化问题的一种最常用方法，其是一种迭代算法。选取适当的初值 x0 ，不断迭代更新： x0→x1→x2…… ，进行目标函数的极小化，直到收敛。由于负梯度方向是使函数值下降最快的方向，因此在迭代的每一步，以负梯度方向更新 x 的值，从而达到减小函数值的目的。不过梯度下降不一定能够找到问题的全局最优解，有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。

深度学习在许多情况下都涉及优化，在诸多的优化问题中最难得就是深度神经网络的训练：寻找深度神经网络上的一组参数 θ ，它能显著地降低代价函数 J(θ) ，该代价函数包含了整个训练集上的性能评估和额外的正则化项（本文主要介绍梯度下降法及其变形，因此不考虑正则化的形式及意义。正则化的东西后续会专门用博客介绍）。通常情况下，对于有 n 个样本的训练集： {(x1,y1),(x2,y2),…,(xn,yn)} ，代价函数可写为训练集上的平均：

J(θ)=E(x,y)∼p̂ dataL(f(x;θ),y)=1n∑i=1nL(f(xi;θ),yi)

其中 L 是每个样本的损失函数（Loss Function）； f(x;θ) 是输入 x 时所预测的输出， y 是目标输出（监督学习）； p̂ data 是训练样本的经验分布，一般假设其为均匀分布。因此关键的一点是如何调整 θ 值，使代价函数 J(θ) 最小化。 J(θ) 构成一个曲面或者曲线，我们的目的是找到该曲面的最低点。根据前面介绍的最速优化原理可知为了快速找到到最优的参数 θ ，需要沿着整个训练集的梯度方向下降。

批量梯度下降法（Batch Gradient Descent, BGD）

批量梯度下降法是梯度下降法最常用的形式。其具体做法就是在更新参数时使用所有的 n 个样本的梯度，这个运算的计算代价是 O(n) 。不过能够保证较好的收敛。

梯度下降（GD）在第 k 个训练迭代的更新：
Require：学习率 ϵ ;
Require：初始参数 θ ;
   While 停止准则未满足 Do
     对于有 n 个样本的训练集： {(x1,y1),(x2,y2),…,(xn,yn)} ，其中 xi 对应的目标输出为 yi ；
     计算梯度估计： ĝ ←1n∑ni=1∇θL(f(xi;θ),yi) ；
     参数更新： θ←θ−ϵĝ  ；
   End While.

小批量梯度下降法（Mini-Batch Gradient Descent, MBGD）

对于深度学习任务，一般都包含几百万、几千万或几亿个训练样本，此时若采用批量梯度下降的话，一次更新需要计算几百万、几千万甚至几亿个次梯度，无论从时间效率还是内存占用来说都是不可取的，一种常用的做法是在算法更新的每一步，只从训练数据中均匀地抽出一小批量（Mini-Batch）样本 {(x1,y1),(x2,y2),…,(xm,ym)} 进行训练。如何选择超参数 m 的值，也是一件令人头疼的事情。因为 m 太大，单次更新梯度的计算量太大； m 太小，迭代的次数和收敛误差（ J(θ)−minθJ(θ) ，即当前代价函数超出最低可能代价的值）均会增加。通常小批量的样本数目 m 是一个相对较小的数，从几十到几百。

批量梯度下降（BGD）在第 k 个训练迭代的更新：
Require：学习率 ϵ ;
Require：初始参数 θ ;
   While 停止准则未满足 Do
     从训练集中采样 m(1<m≪n) 个样本： {(x1,y1),(x2,y2),…,(xm,ym)} ，其中 xi 对应的目标输出为 yi ；
     计算梯度估计： ĝ ←1m∑mi=1∇θL(f(xi;θ),yi) ；
     参数更新： θ←θ−ϵĝ  ；
   End While.

随机梯度下降法（Stochastic Gradient Descent, SGD）

随机梯度下降是小批量梯度下降的一个极端： m=1 ，即每次更新时只用训练集中的一个样本来计算梯度，将参数更新时所需的梯度计算量大大地降低，保证了较高的更新效率。

随机梯度下降（SGD）在第 k 个训练迭代的更新：
Require：学习率 ϵ ;
Require：初始参数 θ ;
   While 停止准则未满足 Do
     从训练集中采样 (xi,yi) ，其中 xi 对应的目标输出为 yi ；
     计算梯度估计： ĝ ←∇θL(f(xi;θ),yi) ；
     参数更新： θ←θ−ϵĝ  ；
   End While.

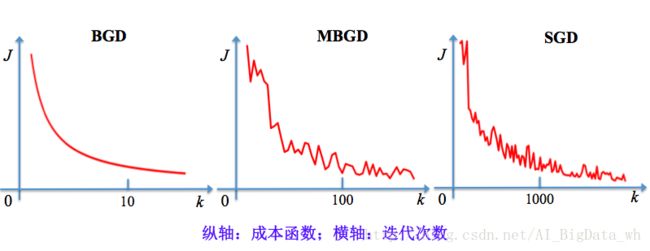
三种梯度下降方法的比较

相比传统的BGD方法，SGD及MBGD一个重要的优势是每一步更新的计算时间不依赖于训练样本数目的多寡，训练速度很快。但在梯度估计时引入了噪声源（部分样本的随机采样），导致迭代方向变化很大，不能很快的收敛到全局或局部最优解，最终 J(θ) 收敛的结果可能是在测试误差的某个固定容差范围内。SGD及MBGD应用于凸问题时， k 步迭代后额外误差量级是 O(1k√) ；对于强凸问题，能到 O(1k) 。在理论上BGD比SGD及MBGD有更好的收敛率。

参考资料

1. http://www.cnblogs.com/pinard/p/5970503.html 梯度下降（Gradient Descent）小结
2. http://blog.csdn.net/zbc1090549839/article/details/38149561 随机梯度下降法
3. http://mooc.study.163.com/smartSpec/detail/1001319001.htm 吴恩达给你的人工智能第一课
4. https://item.jd.com/12128543.html 《深度学习》 [美] Ian，Goodfellow，[加] Yoshua，Bengio，[加] Aaron Courville 著
5. http://item.jd.com/10975302.html 《统计学习方法》 李航
6. https://item.jd.com/11867803.html 《机器学习》 周志华