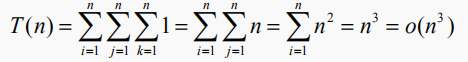数据结构学习笔记-绪论
参考教材《数据结构 C语言第二版 人民邮电出版社》
第一章:绪论
主要知识点:
1.1 数据结构的研究内容
1.2 基本概念和术语
1.3 抽象数据类型的表示与实现
1.4 算法与算法分析
1.1 数据结构的研究内容
一、程序设计的三个层次
1、低层(程序设计):解决数值计算问题。
需求分析—总体设计—模块分割—数学建模—设计算法 —编制程序—调试修改—得到结果
涉及到:数学模型的建立和对应算法的实现
程序=语言+算法
2、中层(数据结构):解决非数值计算问题 或扩充数据类型
程序=语言+数据结构+算法
3、高层(算法设计):解决特殊问题的策略
程序=语言+数据结构+高效算法
二、数据结构举例
1、线性结构:一对一
2、树型结构:一对多
3、图型结构:多对多
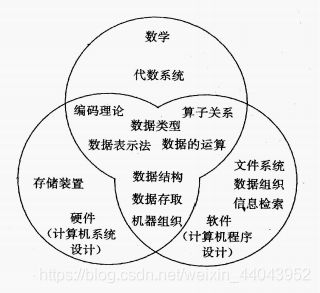
三、《数据结构》的课程地位
介于数学、硬件和软件之间的 一门核心课程
四、《数据结构》的课程目的
1、能够分析研究计算机加工的对象的特性,获得其逻辑结构, 根据需求,选择合适的存储结构及其相应的算法;
2、学习一些常用的算法;
3、复杂程序设计的训练过程,要求程序结构清楚和正确易读;
4、初步掌握算法的时间分析和空间分析技术
1.2 基本概念和术语
一、基本概念
1、数据:客观事物的符号表示,是信息的表现形式,而信息是 数据的内涵。
数据——数据处理——信息
2、数据元素:数据的基本单位,常作为一个整体进行处理。
3、数据项:数据的最小单位。 三者之间的关系:数据 > 数据元素 > 数据项
例:学生表 > 个人记录 > 学号、姓名……
4、数据对象:性质相同的数据元素的集合,是数据的一个子集。
5、数据结构:是相互之间存在一种或多种特定 关系的数据元素的集合。 数据结构是带“结构”的数据元素的集合,“结构”就是指数 据元素之间存在的关系
二、数据的逻辑结构
1、定义:相互之间存在一种或多种特定关系的数据元素的集合,其中数据元素之间的关系,称为“结构”
结构=关系+实体
集合:数据元素同属一个集合
线性结构:存在一对一 的序列相邻关系
树型结构:存在一对多关系的层次关系
图状结构(网状结构) :存在多对多的任意关系
2、形式化定义:二元组 (D,S)
其中D是数据元素的有限集,S是D上关系的有限集
任何关系是笛卡尔积的子集
DS=(D,S)
三、数据的物理结构
1、物理结构:是逻辑结构在存储器中的表示
包括数据元素的表示和关系的表示
2、数据元素的表示
数据元素——元素或结点
数据项——数据域
结点中的数据域连续存储,结点之间可连续也可离散存储
3、关系的表示
顺序存储结构:位置表示关系
链式存储结构:指针表示关系
索引存储
散列存储
4、虚拟存储结构的概念:用已定义的数据类型描述存储结构
四、数据结构的划分
1、按数据结构的性质划分
逻辑结构:数学模型——算法设计
物理结构:存储结构——算法实现
数据结构=逻辑结构(定义&软件)+物理结构(表示&硬件)+运算集合 (实现&数学)
2、按数据结构的存储划分
顺序存储结构:借助元素在存储器的相对位置来表示数据元素 之间的逻辑关系。
链式存储结构:借助指示元素存储地址的指针表示数据元素之 间的逻辑关系。
索引存储方法:在存储结点的同时,还建立附加的索引表,索引表中的每一项称为索引项,形式为:关键字 + 地址
散列存储方法:根据结点的关键字直接计算出结点的存储地址
1.3 抽象数据类型ADT
1、定义:是指基于一个逻辑类型的数据模型以及定义在该模型上的一组操作
ADT=(D,S,P)
每一个操作由它的输入和输出定义
2、与数据类型是相同的概念
数据类型:是值的集合和定义在该集合上的一组操作的总称
数据类型是实现了的数据结构,数据结构是扩充的数据类型
3、抽象与具体的相互对应示例: int a,b;
a和b可以进行+、-、*、/的运算, 而2和6则是具体的int数据
4、抽象数据类型可以通过固有的数据类型(如整型、实型、字 符型等)来表示和实现
1.4 算法和算法分析
一、算法
1、定义:对特定问题求解步骤的描述,指令的有限序列
由基本控制结构(顺序、分支和循环)和原操作(指固有数 据类型的操作)构成。
算法与程序不同!
2、算法的重要特征
(1)有穷性 :能在有穷步后有限时间内执行结束
(2)确定性 :对于相同的输入执行相同路径产生相同的结果(3)可行性 :用于描述算法的操作都是足够基本且已实现
(4)0至多个输入:用形参表示待接收的参数
(5)1至多个输出:没有输出的算法是没有意义的。算法结束 时用返回值或引用类型的形参表示结果
3、算法与数据结构的关系
计算机科学家沃斯提出:
算法+数据结构=程序
揭示了程序设计的本质:选择一种好的数据结构,设计一个好 的算法,就是一个好的程序;
一个算法总是建立在一定数据结构上的;反之,算法不确定, 就无法决定如何构造数据结构
二、算法设计的要求
1、针对算法经常考虑:
是否存在解决问题的算法?
什么是解决问题的“好”的算法?
什么是解决问题的基本
2、“好”的算法应达到以下目标:
(1)正确性(四层含义)
(2)可读性:算法是给人看的
(3)健壮性(容错性):对输入数据的容错性判断
(4)高效性:时间效率与空间效率
3、算法效率的度量
一个算法如果能在所要求的资源限制内将问题解决好,则称这个算法是有效率的
评价标准:
(1)算法所需的计算时间
(2)算法所需的存储空间
(3)算法的简单性
度量算法执行时间的两种方法
(1)事后统计法
有两个缺陷:必须先运行程序;受环境因素影响
(2)事前分析估算法
取决于多个因素:算法策略;问题规模;程序语言;编译质量;执行速度
结论:一个算法“运行工作量”的大小取决于问题的规模
4、时间复杂度
语句的频度:语句重复执行的次数
算法的执行时间是所有原操作执行时间的和
for (i=1;i<=n;++i) //n+1
for (j=1;j<=n;++j) //n*(n+1)
{ c[i][j]=0; //n*n
for (k=1;k<=n;++k) //n*n*(n+1)
c[i][j]+=a[i][k]*b[k][j] }//n*n*n
//T(n)=2n3+3n2+2n+1
问题规模n:算法求解问题的输入量
T(n)与n3同阶的,数量级相同,用O表示
记作:T(n)=O(f(n))=O(n3)
O(n)称作算法的渐进时间复杂度,简称时间复杂度
通常用基本操作的执行频度作为算法的时间度量
a)++x 的频度为1; 常量阶O(1)
{++x; s=0;}
b)++x的频度为n; 线性阶O(n)
for (i=1; i<=n; ++i)
{++x; s+=x;}
c)++x的频度为n2 ; 平方阶O(n2)
for (j=1;j<=n;++j)
for (k=1;k<=n;++k)
{++x; s+=x;}
5、时间复杂度计算方法
(1)最好情形复杂度
(2)最坏情形复杂度
(3)平均情形复杂度 一般多使用最坏情形复杂度。
难以精确给出函数f(n) 时,只需求出关于n的阶即可
例1:N×N矩阵相乘
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{ c[i][j]=0;
for(k=1;k<=n;k++)
c[i][j]=c[i][j]+a[i][k]*b[k][j];
}
for( i=1; i<=n; i++)
for (j=1; j<=i; j++)
for (k=1; k<=j; k++)
x=x+1;
i=1;// ①
while(i<=n)
i=i*2; //②

例4:在数组a[i]中顺序查找值等于e的元素,返回其所在位置
for (i=0;i<n;i++)
if (a[i]==e)
return i+1;
return 0;
最好情况:1次;最坏情况:n次
最坏时间复杂度为:O(n)
结论:有的情况下,算法中基本操作重复执行的次数还随问题的 输入数据集不同而不同
例5 计算f=1!+2!+3!+…+n!
int f=0;
for (i=1;i<=n;++i)
{ w=1;
for (j=1;j<=i;++j)
w=w*j;
f=f+w; }
分析:基本操作为乘法操作,执行次数f(n)=1+2+3+…+n=n(n+1)/2 故:T(n)=O(n2)
例5(改进算法) 计算f=1!+2!+3!+…+n!
w=1; f=0;
for (i=1;i<=n;++i)
{ w=w*i; f=f+w; }
T(n)=O(n)
结论:算法的时间复杂度取决于算法的简单性

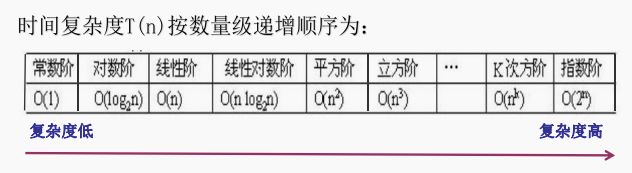
指数时间的关系为:O(2n)
(1)当f(n)为对数函数、幂函数、或它们的乘积时,算法的运行 时间是可以接受的,称这些算法是有效算法;
当f(n)为指数函数或阶乘函数时,算法的运行时间是不可接受的,称这些算法是无效的算法。
(2)随着n值的增大,增长速度各不相同,n足够大时,存在下列关系: 对数函数<幂函数<指数函数
6、空间复杂度算法所占存储空间包括:
(1)存储算法本身所占用的空间
(2)算法的输入 / 输出数据占用的空间
(3)算法在运行过程中临时占用的辅助空间
原则:若输入数据所占空间只取决于问题本身,和算法无关 则只需分析辅助空间;否则应同时考虑输入数据所需空间
原地工作:若辅助空间相对于输入数据量是常数,则称此算 法是原地工作
若所需存储量依赖于特定的输入,按最坏情况来分析