堆的构建, 以及堆排序的c++实现
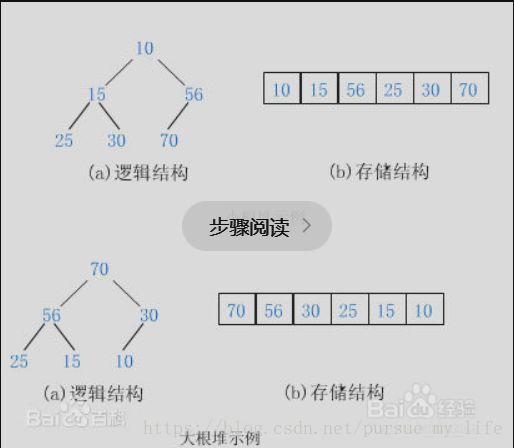
堆是一种数据结构,就是每个节点根据某种规则排序, 从根节点往下都符合某种规律,
根节点的值比所有节点的值都大, 称为最大堆;
根节点的值比所有节点的值都小, 称为最小堆;
堆排序 step:
一)建树部分
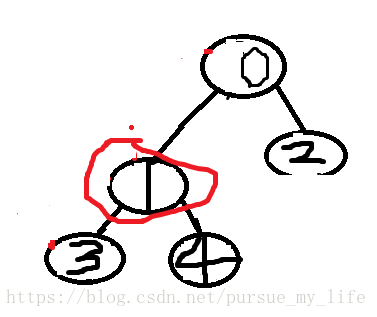
1. 找到一个树的最后一个非叶节点, 计算公式为 (n-1) / 2, 然后遍历树的每个非叶节点,使其符合堆的规则
红圈为最后一个 非叶 子节点
void make_heap(int *a, int len)
{
for(int i = (len-1)/2; i >= 0; --i) //遍历每个 非叶子节点
adjust_heap(a, i, len);//不用考虑那么多, 用面向对象的思乡去考虑,
} //这个函数的作用就是用来使 当前节点的子树 符合 堆的规律2. 要使某节点的当前节点的字数符合 堆规律,需要以下操作:
void adjust_heap(int* a, int node, int size)
{
int left = 2*node + 1;
int right = 2*node + 2;
int max = node;
if( left < size && a[left] > a[max])
max = left;
if( right < size && a[right] > a[max])
max = right;
if(max != node)
{
swap( a[max], a[node]); //交换节点
adjust_heap(a, max, size); 很关于这里递归的解释请看下面
}
}
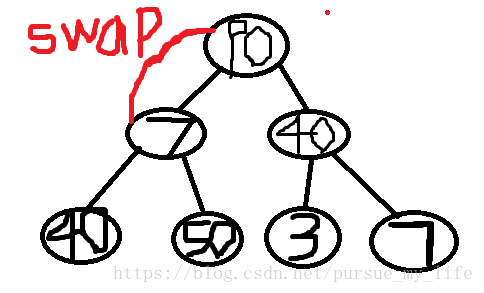
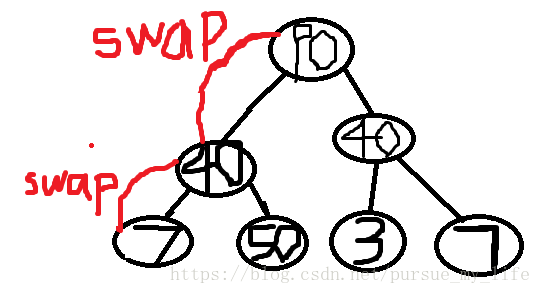
90 和 7交换后, 发现 7 不能管住 原来90的两个儿子, 那怎么办呢??那就继续调用adjust() 让他符合
所以需要递归。
到此为止
这个整个树都符合 堆的规律了, 最大堆就已经建造好了。
二)排序部分
现在我们需要把最大堆中的元素排降序, 该如何呢 ???
将堆的顶部,与最后一个元素交换。 此时除了最后一个元素外, 剩下元素所组成的树已经不是 堆了。(因为此时顶部的元素可能比较小)。 所以, 要将剩下的元素通过 adjust函数调整成 堆。
然后继续将剩余元素中的最后一个元素 与 新堆的顶部交换 。。。。。。
代码如下:
for(int i = len - 1; i >= 0; i--)
{
swap(a[0], a[i]); // 将当前最大的放置到数组末尾
adjust_heap(a, 0 , i); // 将未完成排序的部分继续进行堆排序
}完整代码如下:
#include
using namespace std;
void adjust_heap(int* a, int node, int size)
{
int left = 2*node + 1;
int right = 2*node + 2;
int max = node;
if( left < size && a[left] > a[max])
max = left;
if( right < size && a[right] > a[max])
max = right;
if(max != node)
{
swap( a[max], a[node]);
adjust_heap(a, max, size);
}
}
void heap_sort(int* a, int len)
{
for(int i = len/2 -1; i >= 0; --i)
adjust_heap(a, i, len);
for(int i = len - 1; i >= 0; i--)
{
swap(a[0], a[i]); // 将当前最大的放置到数组末尾
adjust_heap(a, 0 , i); // 将未完成排序的部分继续进行堆排序
}
}
int main()
{
int a[10] = {3, 2, 7, 4, 2, -999, -21, 99, 0, 9 };
int len= sizeof(a) / sizeof(int);
for(int i = 0; i < len; ++i)
cout << a[i] << ' ';
cout << endl;
heap_sort(a, len);
for(int i = 0; i < len; ++i)
cout << a[i] << ' ';
cout << endl;
return 0;
}
然而堆排序中的几个函数,还是可以通过优化来提升 时间复杂度的。比如 adjust()函数的优化
如果在用 adjust在调整最大堆时, 交换需要以下操作:
temp = a[node];
a[node] = a[max];
a[max] = temp;
需要操作三次,100000次 的交换需要操作 300000次。太过于耗时。所以我们可以做类似于插入排序的优化。
if( 节点的某一个儿子 > 节点本身 )
用 temp 把儿子存起来, 并把节点赋值给儿子;
用temp上浮一层到节点的位置, 继续执行判断, 这样一层层不停的上浮。直到不符合条件
if( temp < 同一层的兄弟节点 || temp < 父亲节点)
把 temp 赋值给当前层的元素;
这样省去了每次的交换, 100000的操作只需要操作100000次。大大提高了效率
本人才疏学浅,孤陋寡闻(略去一万字),有错误请指出。