来啃硬骨头——Topk c++ (堆的概念,heapinsert、heapify的过程,在这里描述的很详细)
全文线索:
解题引出topk——> 空间足够时(用vector解)——> 空间不够时(用优先队列解,小顶堆)——> 补充一个topK的题(不用优先队列了,这次自己手写heapinsert和heapify)
一、来解题
/*
给定一个字符串类型的数组arr,求其中出现次数最多的前K个
*/
思路(时间复杂度N(nlogn)):
1、空间足够,则用vector去存,然后用sort排序,输出要求的值。
2、空间不够,利用堆(STL的优先队列默认是实现大顶堆):
1)先利用unordered_map来记录每一个元素出现的次数(键是元素,值是元素出现的次数,因为map里面的键是不可修改的,只能修改值。map中重载了[],可以利用[]来实现键值对的插入,因为map会查找【】里面的键,如果不存在该键,则会创建该键的键值对,具体可以去看《stl源码剖析》里面的map)。
2)再利用优先队列来实现存储k个元素,堆的大小不超过k。每次来一个元素,如果堆不满,则插入堆中,如果堆满(就是堆中元素等于k个的时候)就将元素和堆顶进行比较,如果新来的元素是出现次数超过堆顶,则将堆顶弹出,将新元素插入堆。
用到的知识:
仿函数(就是利用优先队列的解法里面的compare,仿函数可以看看《STL源码剖析》第七章.优先队列的源码里写了,第三个参数是一个类名;sort里面的第三个参数不是类名,注意看源码)、优先队列、堆、vector
二、利用vector和sort的解法
/*
给定一个字符串类型的数组arr,求其中出现次数最多的前K个
*/
#include
#include
#include
#include
using namespace std;
struct Node{
string key;
int val;
Node(string i, int j):key(i),val(j){}
};
struct compare{
bool operator()(Node i, Node j){
return i.val>j.val;
}
};
void TopKTimes(vector&con, int k){
if((k<0)||!con.size()) return;
unordered_mapcount;
for(auto i: con){
if(count.find(i)==count.end())
count[i]=1;
else
count[i]++;
}
vectorres;
for(auto i : count){
Node cur(i.first, i.second);
res.push_back(cur);
}
compare com;
sort(res.begin(), res.end(), com);
for(int i=0; icon=
{"abcdefg", "qwerty", "asdfgh", "zxcvbn", "abcdefg","abcdefg","qwerty"};
int k=3;
while(k){
cout<<"k="<
运行结果:
三、利用优先队列的解法
/*
给定一个字符串类型的数组arr,求其中出现次数最多的前K个
*/
#include
#include
#include
#include
#include
using namespace std;
struct Node{
string key;
int val;
Node(string i, int j):key(i),val(j){}
};
struct compare{
bool operator()(const Node& cur1, const Node& cur2){
return cur1.val>cur2.val;
}
};
void TopKTimes(vector&con, int k){
if(con.empty()) return;
unordered_mapcount;
priority_queue,compare> minHeap;
for(int i=0; i=count.size()){
for(auto i: count)
cout<minHeap.top().val){
minHeap.pop();
minHeap.push(cur);
}
}
}
while(minHeap.size()>0){
cout<con={"abcdefg", "qwerty", "asdfgh", "zxcvbn", "abcdefg","abcdefg","qwerty"};
int k=3;
while(k){
cout<<"k="<
运行结果
————————————————————————————————————————————————————
2018.12.27
四、补充一道不知道是哪家的真题(不用优先队列解了)
设计并实现TopKRecord结构,可以不断地向其中加入字符串,并且可以根据字符串出现的情况随时打印加入次数最多的前k个字符串。具体为:
- 1)k在TopKRecord实例生成时指定,并且不再变化(k是构造TopKRecord的参数)。
- 2)含有 add(String str)方法,即向TopKRecord中加入字符串。
- 3)含有 printTopK()方法,即打印加入次数最多的前k个字符串,打印有哪些字符串和对应的次数即可,不要求严格按排名顺序打印。
- 4)如果在出现次数最多的前k个字符串中,最后一名的字符串有多个,比如现次数最多的前3个字符串具体排名为:A 100次 B 90次 C 80次 D 80次 E 80次,其他任何字符串出现次数都不超过80次
那么只需要打印3个,打印ABC、ABD、ABE都可以。也就是说可以随意抛弃最后一名,只要求打印k个
要求:
- 1)在任何时候,add 方法的时间复杂度不超过 O(logk)
- 2)在任何时候,printTopK方法的时间复杂度不超过O(k)。
思路:
写一个类,类里面需要一个hash来记录每个字符串出现的次数,然后自己写个堆(实际上就是个数组)来实现heapinsert和heapify操作,然后还要一个hash,记录每个字符串在堆中的索引位置(就是那个数组中的索引位置,堆其实是假想的,实际是个数组,看下面的就懂了)。
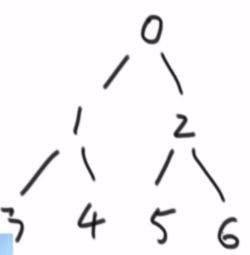
先来复习一下堆
堆是一棵完全二叉树(满二叉树的每一层都是满的,完全二叉树允许叶节点那一层是节点不满,但是节点必须从左到右的排布,中间出现空缺,就不是完全二叉树了,如下图中左侧为完全二叉树,右侧就不是)
堆是通过数组来实现的。
i 位置的(如下图所示,画成图好记一点)
- 左孩子的下标是 2*i+1 ,
- 右孩子的下标是 2*i+2 .(前提是不越界)。
- i 节点的父节点下标为 (i-1)/2 。
从始至终只有数组结构,堆是脑补出来的结构,自始至终真实存在的只有数组。
堆分为两种:大根堆和小根堆
1、如何把数组调整成一棵大根堆
heapinsert原理——每次都与父节点进行比较
将数组中的数字依次加入到堆中。对于每一个加入到堆中的数字,将其与其父节点的值进行比较,如果他大,则将他和他父节点的值进行交换。他的索引位置为 i ,则其父节点的索引位置为 (i-1)/2 。
注:-1/2的结果为0,所以index=0的时候也不用怕
#include
#include
using namespace std;
void heapinsert(vector&nums){
if(!nums.size()) return;
int temp=0, index=0;
for(int i=0; inums[(index-1)/2]){
temp=nums[index];
nums[index]=nums[(index-1)/2];
nums[(index-1)/2]=temp;
index=(index-1)/2;
}
}
for(auto i:nums)
cout<nums={1,2,3,4,5,6,7,8,9};
heapinsert(nums);
return 0;
}
运行结果:
分析建立大根堆过程的复杂度
当一个数加进来,他最多只和这棵树的高度个数进行比较(调整)。任何一个点加进来,我只和我沿途的这些个点进行比较,和其他的点没什么关系
建立一个大根堆的时间复杂度是O(N)=log1+log2+...+log(N-1)
heapify过程——每次都与子节点进行比较
堆中某个值发生了变化,如何调整。
比如大根堆中,索引位置为 i 的元素的值发生了改变(变小),则将其与左右两个孩子进行比较,将其与较大的孩子进行交换。 左孩子的索引位置为 2*i+1 , 右孩子的索引位置为 2*i+2.
#include
#include
using namespace std;
void heapinsert(vector&nums){
if(!nums.size()) return;
int largest=0, i=0, temp=0;
for(int index=0; indexnums[2*i+2]?2*i+1:2*i+2
:2*i+1;
//说明nums[i]已经不能再向下移动了
if(nums[i]>=nums[largest]) break;
//交换两个元素的值
temp=nums[i];
nums[i]=nums[largest];
nums[largest]=temp;
//此时该继续向下比较了
i=largest;
}
}
for(auto i:nums)
cout<nums={1,9,8,7,6,5,4,3,2};
heapinsert(nums);
return 0;
}
运行结果