2020 牛客暑期训练营补题（第一场）

暑假还是不能摸鱼了，尽量每天补一道题。

这里大部分的补题应该都是参考了大佬的题解，所以如果有大佬看到了自己的解法，请多多包涵。

A题

题目描述

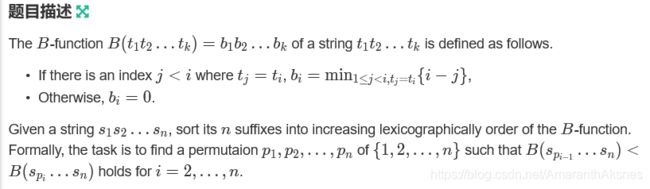
（这个题当时我是看了半天看不懂要做什么，看题解的时候也是一知半解。还好最后还是把意思搞懂了）

该题就是告诉你字符串的长度n，给你一个字符串。然后从后缀看，整出n个长度分别为1、2、3、……、n的字符串。打个比方：abba 按后缀从1到n 分别为 a ba bba abba。
将这些数组按照题中B数组的方式处理。
将这些新字符串按字典序排序，从大到小排列。因为长度都不同，就用他们的长度表示字符串 输出排序的结果。

题目思路

这个题目当时直播讲题的时候全英文题解也是看懵了，只好老实看大佬题解翻译。这道题关键涉及一个后缀数组的结论。

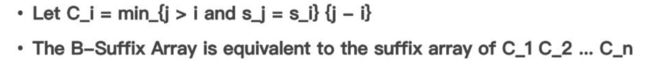
这个结论正好符合原字符串中只有两种字符的情况。根据这个结论来写出对应代码。

代码

#include
using namespace std;
#define ll long long
const int maxn=2e5+100;
const ll mod=1e9+7;
int n,m,k,t;
char s[maxn];
int c[maxn],sa[maxn],rk[maxn],tmp[maxn];
int cmp(int x,int y)
{
    if(rk[x]!=rk[y])
	return rk[x]<rk[y];
    else
    {
        int rx,ry;
        if(x+k<=n)rx=rk[x+k];
        else rx=-1;
        if(y+k<=n)ry=rk[y+k];
        else ry=-1;
        return rx<ry;
    }
}
void getsa(int sa[])
{
    rk[n]=-1;
    sa[n]=n;
    for(int i=0;i<n;i++)
   {
        sa[i]=i;
        rk[i]=c[i];
    }
    for(k=1;k<=n;k*=2)
   {
        sort(sa,sa+n+1,cmp);
        tmp[sa[0]]=0;
        for(int i=1;i<=n;i++)
       {
            if(cmp(sa[i-1],sa[i]))
                tmp[sa[i]]=tmp[sa[i-1]]+1;
            else
                tmp[sa[i]]=tmp[sa[i-1]];
        }
        for(int i=0;i<=n;i++)
            rk[i]=tmp[i];
    }
}
int main(){
    while(~scanf("%d",&n))
   {
        scanf("%s",s);
        int a=n,b=n;
        for(int i=n-1;i>=0;i--)
       {
            if(s[i]=='a')
           {
                if(a==n)
               		c[i]=(n-a)%n;
                else 
               		c[i]=(n-a+i)%n;
                a=i;
            }
            else
           {
                if(b==n)
                	c[i]=(n-b)%n;
                else 
                	c[i]=(n-b+i)%n;
                b=i;
            }
        }
        getsa(sa);
        for(int i=1;i<=n;i++)
       		printf("%d ",sa[i]+1);
       	printf("\n");
   }
   return 0;
}

F题

（这道题目当时小队成员过的，自己还没想完就过了，我只帮助了一下debug）

题目意思：给你两个字符串，它们如同无限循环小数一般无限长。试比较它们的字典序大小。

这道题基本上第一眼都会想到把它们长度拉到最小公倍数比较。看一下数据稍微计算一下会发现这样行不通，会爆。看了一下题解发现大多数人第一时间想出的能解题的算法都是找出最小循环节，结束后发现可以直接比较a+b和b+a的字典序。

下面我自己再推一下：

a+b和b+a的比较情况需要有一种转化的思想。

假设a.size<=b.size;

1.如果单次可比较部分都相同 size相同的时候：=；size不等于的时候 a较短，b补上。由于前面比较部分相同，b这时前面的部分可看作是a的前面部分，当b比完了，a接上，a的前面部分可看作是b。

2.单次可比较部分不同：字典序单次比较后输出

#include
using namespace std;
string a,b,s1,s2;

int main()
{
	while(cin >> a >> b)
	{	
		s1=a+b;	
		s2=b+a;
		if(s1==s2)		puts("=");
		else if(s1>s2)		puts(">");		
		else			puts("<");
	}		
	return 0;
}

I题

题目大意：输入到文件末尾。给出一些点和连接他们的边，能否实现选择其中一些边使每个点的度与给出的d_i数组对应。是则输出“Yes”，否则输出“No”。

这道题当时和队友想的时候理解错了题目意思，以为是所有的边都选择看是否符合题意。按照这个思路写居然还能过示例，交了好几次wa才发现some of（英语基础8行）

然后有了这个选择的操作，这道题一下子变得没有想象中那么容易。以至于结束了也没有继续完善出来。

自己后来想了一下也没有想出来，于是看了一下大佬的代码，发现涉及的知识点了解的不多（一般图最大匹配，带花树）。目前只能先看完知识点再继续补。

J题

这道题题目还是能看懂，过的人也挺多。吃了高数学的不行的亏

读题思考想法：先求出积分化简结果，再求出mod意义下的值。

积分过程：

（每步阶乘计算的时候要处理一下）

#include
using namespace std;  
typedef long long ll; 
int const N=2e6+10;  // n的范围到1e6 但是式子分母中有2n+1 所以N取到2倍多 
int const M=998244353;
int f[N],n;  
int ksm(int x,int y)
{
    int res=1;  
    while (y) 
 {
        if(y&1) res=1ll*res*x%M;  
        y>>=1; 
        x=1ll*x*x%M;  
    }
    return res;  
}
int main()
{
    f[0]=1;  
    for(int i=1;i<N;i++)     //存阶乘 
        f[i]=1ll*f[i-1]*i%M;  
    while (scanf("%d",&n)==1)
    {
        printf("%d\n",1ll*f[n]*f[n]%M *ksm(f[2*n+1],M-2)%M);  
    }
    return 0; 
}

本题知识点：积分、分数取模。