一本通提高篇 KMP算法

扯淡

这么想想 初中时第一次到高中部听学长讲课就是$KMP$ 看毛片算法
还是大哥$Michael\_Bryant$给我讲的呢 那应该是我跟大哥第一次奔现 正式见面
(他还搂了我好几下 现在我抱他他还说我$gay？$
行了不搞了 说正事吧

$KMP$算法

$KMP$算法是用来处理字符串匹配问题的，由$D.E.Knuth，J.H.Morris$和$V.R.Pratt$共同提出的。字符串匹配就是给你个大串$A$和小串$B$，让你求$A$中出现了几次$B$。其中如果$A$中有$B$，那么我们就称$B$是$A$的子串。

算法流程

假如，$A=abababaababacb,B=ababacb$,我们来看一看$KMP$是怎么工作的。我们用两个指针$i$和$j$分别表示，$A[i-j+1...i]$与$B[1...j]$完全相等。也就是说，$i$是不断增加的，随着$i$的增加,$j$相应地变化，且$j$满足以$A[i]$结尾的长度为$i$的字符串正好匹配$B$的前$j$个字符，现在需要检验$A[i+1]$和$B[j+1]$的关系。当$A[i+1]=B[j+1]$时，$i$和$j$各加一；当$j=m$时，我们就说$B$是$A$的子串($B$串已经完全匹配了)，并且可以根据这时的值算出匹配的位置。当$A[i+1]\ne B[j+1]$，$KMP$的策略是调整$j$的位置(减小$j$值)使得$A[i-j+1...i]$与$B[1...j]$保持匹配且尝试匹配新的$A[i+1]$与
与$B[j+1]$。
口胡了这么多 相信你肯定也是一脸懵 先不说流程听没听懂 怎么代码实现啊!!??
真正演示一遍才能得出真正的答案 $bilibili$上有个大哥讲的可好了 我第二次听$KMP$就是跟他学的

传送门
$okk$看完了相信你一定会了 那么我们直接上题吧
诶诶别揍我 哥我错了
先粘一道洛谷的模板题
P3375 【模板】KMP字符串匹配
分两步走 先求$next$数组再进行$KMP$
需要注意到的是 跟视频不同的一点 我们的$next$数组整体右移了一位，这样不仅方便求解$next$数组，在$KMP$匹配中我们也不用调用前一位的$next$值
求解$next$数组：

void get_nxt(){
	int j=0;
	for(int i=1;i<l2;i++){
		while(j&&s2[i+1]!=s2[j+1])j=nxt[j];
		if(s2[i+1]==s2[j+1])nxt[i+1]=++j;
	}
}

都说可以把求解$next$数组理解成自我匹配，但我感觉更像一个贪心算法
下面是$KMP$的过程:

int j=0;
for(int i=0;i<l1;i++){
	while(j&&s1[i+1]!=s2[j+1])j=nxt[j];
	if(s1[i+1]==s2[j+1])j++;
	if(j==l2){
		j=nxt[j];
		printf("%d\n",i+2-l2);
	}
}

没什么好说的 视频里说的真是太详细了 除了字幕是机翻之外真没啥毛病
上这个题的代码:

#include
using namespace std;
#define N int(1e6+100)
char s1[N],s2[N];
int l1,l2,nxt[N];
void get_nxt(){
	int j=0;
	for(int i=1;i<l2;i++){
		while(j&&s2[i+1]!=s2[j+1])j=nxt[j];
		if(s2[i+1]==s2[j+1])nxt[i+1]=++j;
	}
}
int main(){
	scanf("%s%s",s1+1,s2+1);
	l1=strlen(s1+1),l2=strlen(s2+1);
	get_nxt();
	int j=0;
	for(int i=0;i<l1;i++){
		while(j&&s1[i+1]!=s2[j+1])j=nxt[j];
		if(s1[i+1]==s2[j+1])j++;
		if(j==l2){
			j=nxt[j];
			printf("%d\n",i+2-l2);
		}
	}
	for(int i=1;i<=l2;i++)printf("%d ",nxt[i]);
	putchar(10);
}

看了看网上的题解 自认为写的算是比较简洁的了
那么现在我们上一本通里的题吧:

剪花布条

题目描述
一块花布条，里面有些图案，另有一块直接可用的小饰条，里面也有一些图案。对于给定的花布条和小饰条，计算一下能从花布条中尽可能剪出几块小饰条来呢？
输入
输入中含有一些数据，分别是成对出现的花布条和小饰条，其布条都是用可见ASCII字符表示的，可见的ASCII字符有多少个，布条的花纹也有多少种花样。花纹条和小饰条不会超过1000个字符长。如果遇见#字符，则不再进行工作。
输出
输出能从花纹布中剪出的最多小饰条个数，如果一块都没有，那就老老实实输出0，每个结果之间应换行
样例输入
abcde a3
aaaaaa aa

样例输出
0
3
提示
你猜
$Solution:KMP$果题 注意细节就是花布条剪完了就不能再匹配了，所以相较模板要把匹配时的$j=nxt[j]$改成$j=0$

#include
using namespace std;
#define N 1010
int l1,l2,nxt[N];
char s1[N],s2[N];
inline void get_nxt(){
	int j=0;
	for(int i=1;i<l2;i++){
		while(j&&s2[i+1]!=s2[j+1])j=nxt[j];
		if(s2[i+1]==s2[j+1])nxt[i+1]=++j;
	}
}
int main(){
	while(scanf("%s",s1+1)){
		if(s1[1]=='#')return 0;
		scanf("%s",s2+1);
		l1=strlen(s1+1),l2=strlen(s2+1);
		get_nxt();
		int j=0,ans=0;
		for(int i=0;i<l1;i++){
			while(j&&s1[i+1]!=s2[j+1])j=nxt[j];
			if(s1[i+1]==s2[j+1])j++;
			if(j==l2)j=0,ans++;
		}
		printf("%d\n",ans);
	}
}

Radio Transmission

题面
$Solution:$手动写写画画不难发现$n-nxt[n]$的值就是答案

#include
using namespace std;
#define N int(1e6+100)
int n,nxt[N];
char s[N];
void get_nxt(){
	int j=0;
	for(int i=1;i<n;i++){
		while(j&&s[i+1]!=s[j+1])j=nxt[j];
		if(s[i+1]==s[j+1])nxt[i+1]=++j;
	}
}
int main(){
	scanf("%d%s",&n,s+1);
	get_nxt();
	printf("%d\n",n-nxt[n]);
}

Periods of Words

题面
$Solution:$本题的考察点主要是阅读理解 其次是$KMP$算法
将题面转换成类人话：
一个字符串$A$ 它的一个子串$B$如果满足$A$是$BB$的子串 就称$B$是$A$ 的一个周期。如下图

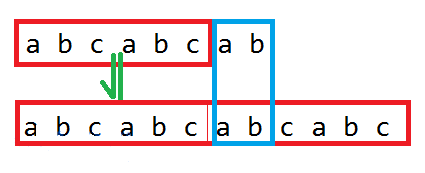
给定一个字符串，求它的所有前缀的最大周期长度之和

这个题要用到$nxt$数组的一个性质：长度为$nxt[i]$的前缀和后缀相等

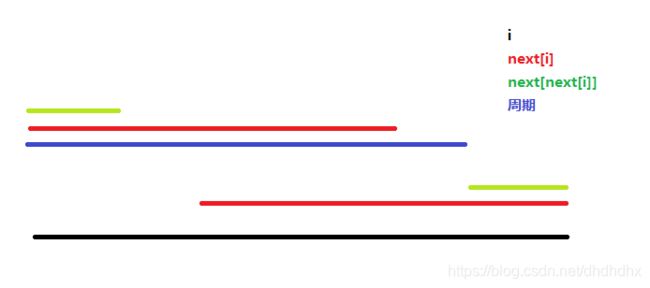
那么不难发现 如果长度为$i$字符串$A$的长度为$nxt[i]$的前缀有一个长度为$j$的前后缀 那么字符串 $A$就有一个长度为$i-j$的周期
所以对于每一个前缀$i$我们要找到最小的$j$ 周期$i-j$最大
那就每次递归到$0$之前的一个$nxt$数组的值 显然这时候的$j$最小

好像还有一个很可行的优化 就是每次找到 $j$之后 直接把$nxt[i]$改成$j$，就像并查集路径压缩一样
因为现在我们不匹配，不需要让$nxt$数组最大来保持时间复杂度，反而$nxt$数组越小递归层数越小时间复杂度越优
$PS.$建议开$longlong$，其实可以试试不开的！

#include
using namespace std;
#define N int(1e6+100)
#define reg register
int n,nxt[N];
char s[N];
long long ans;
void get_nxt(){
	int j=0;
	for(reg int i=1;i<n;i++){
		while(j&&s[i+1]!=s[j+1])j=nxt[j];
		if(s[i+1]==s[j+1])nxt[i+1]=++j;
	}
}
int main(){
	scanf("%d%s",&n,s+1);
	get_nxt();
	for(reg int i=2;i<=n;i++){
		int j=i;
		while(nxt[j])j=nxt[j];
		if(nxt[i])nxt[i]=j;
		ans+=i-j;
	}
	printf("%lld\n",ans);
}

似乎在梦中见过的样子

题面
哇这个题真的狗
我想了差不多一天多的时间
首先想到的是$O(n^3)$的做法 枚举每个左端点 在求$nxt$值的过程中枚举右端点 对于每个子串 递归$nxt$当$j=nxt$时 如果满足$k\le j$且$2j<i$，那么$ans++$
这显然是$O(n^3)$的算法 那么我们怎么优化一下呢？

跟上一道题一样 对于每次递归 我们可以相当于给他路径压缩一下
设 $f[x]$为在右端点为$x$时 可以满足条件的最小的长度 如果没有则为$inf$
那么我们每次更新$f[x]=min\{x,f[nxt[x]]\}$ 这样显然可以$O(1)$转移和求值 复杂度就降到了$O(n^2)$
代码

#include
using namespace std;
#define N 20000
#define reg register
#define ll long long
char s[N];
int n,k,f[N],nxt[N];
ll ans;
int get(char *s)
{
    int j=0,sum=0;f[0]=1e9;
    for (int i=2;s[i];i++){
        while (j>0&&s[i]!=s[j+1]) j=nxt[j];
        nxt[i]=j+=s[i]==s[j+1];
        if (j<k) f[j]=1e9;else f[j]=min(j,f[nxt[j]]);
        if (f[j]<<1<i) sum++;
    }
    return sum;
}
int main(){
	scanf("%s%d",s+1,&k);
	n=strlen(s+1);
	for(reg int i=0;i<n;i++)ans+=get(s+i);
	printf("%lld\n",ans);
}

什么傻逼玩意 调了一个小时 艹

Censoring

题面
听说是$kmp$加栈 但是我不想打 心情极度不爽 现在只想打哈希
算了 哈希也得加栈 写$KMP$吧
记录一个$f[i]$表示$i$这里能匹配到的最大的$j$
栈里放的是数组下标 每次如果成功匹配到就把$top-=len$，$j=f[top]$
完事 上代码

#include
using namespace std;
#define N int(1e6+100)
#define reg register
char s1[N],s2[N];
int top,l1,l2,f[N],nxt[N],stk[N];
void get_nxt(){
	int j=0;
	for(reg int i=1;i<l2;i++){
		while(j&&s2[i+1]!=s2[j+1])j=nxt[j];
		if(s2[i+1]==s2[j+1])nxt[i+1]=++j;
	}
}
int main(){
	scanf("%s%s",s1+1,s2+1);
	l1=strlen(s1+1),l2=strlen(s2+1);
	get_nxt();
	int j=0;
	for(reg int i=1;i<=l1;i++){
		while(j&&s1[i]!=s2[j+1])j=nxt[j];
		if(s1[i]==s2[j+1])j++;
		f[i]=j,stk[++top]=i;
		if(j==l2)top-=l2,j=f[stk[top]];
	}
	for(int i=1;i<=top;i++)printf("%c",s1[stk[i]]);
}

唉做完这道题其实我心里挺不是滋味的

还记得当时贯通部来高中上体验课时 那时刚在高中网站拿到账号时 自己因为有$OI$基础所以刷题数比大家都多
后来$nsy$把我超了 然后那天我一下子超过他$50$多道题哈哈哈
还开玩笑说 你超我一道 我超你十道 $hhh$想想那时课真是快乐
再后来 牛哥好像钟爱上了动态规划 加上自己主动&被动刷水题 网站名次早就落得我远远的 (其实他有抄代码的嫌疑
再再后来 我也进入了颓废不学习不做题的初二 自从那年过去 我再也没能有机会在榜上的排名骄傲起来 但是我也没因为这个虚心学习…真是可惜hhh
今天做完这五道题刚好超了牛哥 如果不是意外的话 想想以牛哥找水题的速度 我应该一天就被拉出去好几道题哈哈
2333 人生无常 珍惜现在
希望大家都能有个好的未来吧…
)//有左括号不能没有右括号

总结

$KMP$算法是一个很牛掰的算法 但是真考验思维…想到正解你会发现$KMP$这么有用！ 想不到正解你会认为$KMP$真是垃圾
$PS:$今天$11.26$祝我们的宝贝儿$lyss$生日快乐!!!
连续两晚加班终于搞完了
尽请关注下一章的$trie$树 可能以后会越来越墨迹 我可能会跳章写