深度学习系列八：支持向量机

前言

支持向量机（SVM）是机器学习中非常重要的一个算法，虽然在今天，它在很多应用层面被神经网络取代了，但其实现仍然有很多值得学习的地方，而且相比较于神经网络的黑盒子特性，其解释性要好很多，训练的过程也相对更快。

从线性回归出发

本系列开篇讲过了线性规划，原始的SVM也是线性回归问题，考虑一个二分类问题：$x\in X，y\in \{1,-1\}$，我们建立一个线性模型：
$$f(x)=w^{T}x+b$$

判别函数为：
$$y=sign(f(x))$$
在这个二分类问题中，显然存在一个分割超平面$w^{T}x+b=0$将样本进行了分割，f(x)>0的样本为一类，f(x<0)的为另一类，以一个二维的例子画图直观的看一下（图来源于《神经网络与深度学习》，邱锡鹏）：

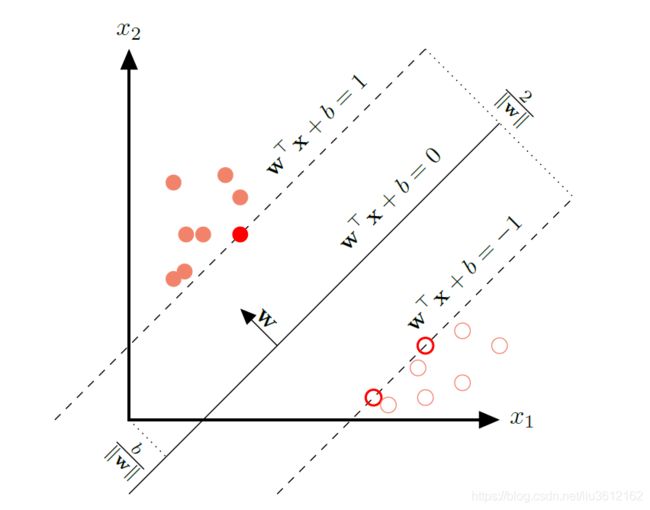
从图中可以比较明显的看出，当分割超平面与两类样本点都比较远时，分割会更加稳定，泛化性能会更好，这里就引出了SVM的优化目标：最大化间隔。这里详细说明一下：
对空间几何有了解的都知道，对任意样本点$x_i$，它与平面$w^{T}x+b=0$的垂直距离为：$d_i=\frac{||w^T{x}_i+b||}{||w||}=\frac{y_i(w^T{x}_i+b)}{||w||}$
于是令：
$$\gamma =min\{d_0,d_1...d_n\}$$
SVM的优化目标就变成了：$\underset{w,b}{\max }\gamma$
把问题用数学公式写一遍：
$$\begin{array}{rl}& \underset{w,b}{\max }\gamma \\ & \text{ s.t. }\frac{y_i(w^T{x}_i+b)}{||w||}\ge \gamma ,\forall i\end{array}$$
针对模型中的待优化参数w和b，可以看出，对其进行任意非零scale后该分割超平面保持不变，因此可以令：$||w||\ast \gamma =1$，原问题可以做适当转化变为：
$$\begin{array}{rl}& \underset{w,b}{\min }\frac{1}{2}||w|{|}^2\\ & \text{ s.t. }1-y_i(w^T{x}_i+b)\le 0,\forall i\end{array}$$
剩下的就是使用拉格朗日乘数法进行求解的部分，构造拉格朗日函数：
$$\Lambda (w,b,{\lambda }_i)=\frac{1}{2}||w|{|}^2+\sum _i{\lambda }_i(1-y_i(w^T{x}_i+b))$$
本问题满足强对偶条件，因此可以将其转为拉格朗日对偶问题进行求解，拉格朗日算法以及用于优化的SMO算法很多文章有详述，这里就不多讲了。

软间隔

以上的方式仅针对线性可分的问题适用，如果遇到线性不可分问题，例如如下的样本：

图中所举例子比较极端，但比较容易理解，如第一张图所示，如果样本不是线性可分的，哪怕只有一个类的样本中出现了一个叛徒，这时候我们用上面的方法计算得到的分割超平面可能会变成下图这样：

如果不是有什么特殊需求，一般而言我们认为第一张图的分割更加合理一些，因为第二张图的分割结果不但没有办法处理异常样本，而且分割稳定性也差很多，会出现不少的误分割，如何避免这种因为少量异常样本导致分类稳定性大幅下降的情况，或者说在一些线性不可分的问题中需要尽可能取得更好的分割模型，就是软间隔所需要做的了。
考虑图中的极端例子，如果我们能够将图中$x_i$按虚线反向平移$\xi$，再进行之前的分割计算，不就可以解决问题了么，因此，我们在之前的式子中引入松弛变量（slack variable）$\xi$，那么约束条件就变成了：
$$\text{ s.t. }\frac{y_i(w^T{x}_i+b)}{||w||}\ge \gamma -{\xi }_i,\forall i,{\xi }_i>0$$
怎么理解这个式子呢，其实就是允许一些样本与分割超平面的距离适当小于$\gamma$，也可以理解成将部分样本与分割超平面的距离进行一定的补偿再参与计算最小距离$\gamma$，例如上图中的$x_i$，把它与最优分割超平面的具体补偿$\xi$再进行正常的优化。
当然如果仅仅是这样上面的优化问题是无法计算的，因此可以令$\xi \to +\infty$，则$\gamma \to +\infty$，因此需要针对$\xi$作一些惩罚，通俗理解就是，做出尽可能小的补偿，再去最大化$\gamma$，因此最终的公式变成了：
$$\begin{array}{rl}& \underset{w,b}{\min }\frac{1}{2}||w|{|}^2+C\sum _i{\xi }_i\\ & \text{ s.t. }1-y_i(w^T{x}_i+b)-{\xi }_i\le 0,\forall i,{\xi }_i>0\end{array}$$
系数C用来调节惩罚项的力度，${\xi }_i$代表针对每个样本的补偿值，之后的计算与之前的完全一致。软间隔机制实质上就是选择忽略或者减小那些少量的难以区分的样本的影响，来得到一个尽可能稳定的分割超平面。

核函数

同样为了解决一些线性不可分的问题，于是将原来的样本空间转换到一个高维线性可分空间中，再进行分类，令这个将样本由低维空间转换到高维空间的函数为$\Phi (x)$，于是模型变成了：
$$g(x)=w^{\prime T}\Phi (x)+b$$
这里$w^{\prime }$为在高维空间的权重参数，令$\Phi (X)$为高维空间的一组基，于是$w^{\prime }={\sum }_i{\alpha }_i\Phi (x_i)$，于是上式为：
$$g(x)=\sum _i{\alpha }_i\Phi (x_i{)}^T\Phi (x)+b$$
这个式子可以这样理解，对于任意一个x，计算得到$\Phi (x_i{)}^T\Phi (x),\forall i$，若训练样本包含n的样本，则可以得到一个n维向量$K=\{\Phi (x_0{)}^T\Phi (x),\Phi (x_1{)}^T\Phi (x)...\Phi (x_n{)}^T\Phi (x){\}}^T$，于是上式转换为：
$$g(x)={\alpha }^{T}K+b$$
对比f(x)函数，可以将$\alpha$与w对应，K与x对应，其余的训练优化步骤完全与前文一致。仔细观察上述的流程可以发现，我们并不需要知道$\Phi (x)$的具体形式，而需要知道$\Phi (x_i)\Phi (x_j)$，也就是核函数：
$$K(x_i,x_j)=\Phi (x_i)\Phi (x_j)$$
常用的核函数例如高斯核函数、点积核等等。