NOI2018 D1T1 题解

传送门

首先，预处理每个点到1号点的最短距离$dist$（它等于1号点到每个点的最短距离）。注意：**SPFA死了！**可以用堆优化Dijkstra。

然后我们就把问题转换成了：从一个点出发，只经过海拔大于某个值的边，能到达的点中$dist$的最小值。

这个问题怎么解决呢？有请Kruksal重构树出场！

什么是Kruskal重构树？

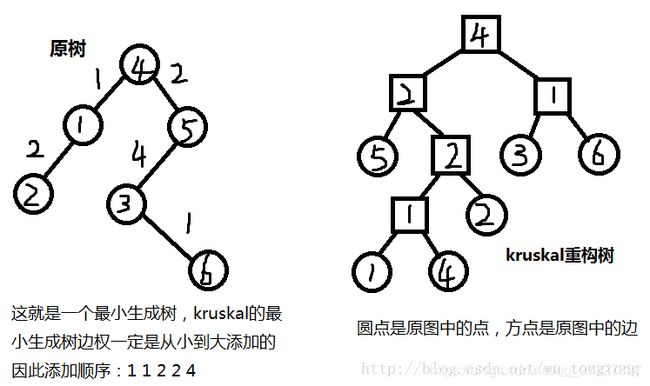
有点像并查集，但不同的是在Kruskal求最小生成树时，每次加边成功时就建一个新点代表这条边，这条边的两个端点所在集合的根的父亲连向这条边代表的点。如下图：（借用了别人的图）

![1.png](1.png

可以看出最小生成树的Kruskal重构树有以下性质：

• 二叉树
• 一个方点代表的边权$\le$它父亲代表的边权
• 两个点之间的最小瓶颈路（路径上边权最大值最小的路）=它们在Kruskal重构树上lca的边权

在本题中，起点可以到达某一个点当且仅当它们的lca的边权可以行走。

所以可以预处理每个点子树中的$dist$中最小值，查询时从起点向上走，走到最上面的可以走的边代表的点，那个点子树中的$dist$中最小值就是答案。

走可以改成倍增跳。

//sro zbw ak noi2018 orz o(*￣▽￣*)o
#include
using namespace std;
#define pb push_back
#define clr(a) memset(a,0,sizeof(a))
const int N=500005,N2=N<<1,inf=0x3f3f3f3f;
int n,m,d[N2],mn[N2],vis[N],t,fa[N2][20],uf[N2],lust,Q,k,s;
struct node{int d,n;};
bool operator<(node a,node b){return b.d<a.d;}
priority_queue<node>q;
vector<int>e[N],f[N];
struct edge{int u,v,w,x;}ed[N2];
bool cmp(edge a,edge b){return b.x<a.x;}
void init();
int find(int a){if(uf[a])return uf[a]=find(uf[a]);return a;}
void build(){clr(fa),clr(uf),clr(mn);
    for(int i=1;i<=n;i++)mn[i]=inf;
    for(int i=0,j=n;i<m;i++){
        int v=find(ed[i].v),u=find(ed[i].u);
        if(v==u)continue;
        uf[v]=uf[u]=++j,fa[v][0]=fa[u][0]=j,d[j]=inf,mn[j]=ed[i].x;
    }n=(n<<1)-1;
    for(int i=1;i<=n;i++)
        d[fa[i][0]]=min(d[fa[i][0]],d[i]),mn[fa[i][0]]=min(mn[fa[i][0]],mn[i]);
    for(int k=1;k<20;k++)for(int i=1;i<=n;i++)fa[i][k]=fa[fa[i][k-1]][k-1];
}
void solve(){lust=0;
    scanf("%d%d%d",&Q,&k,&s);
    while(Q--){
        int a,b;scanf("%d%d",&a,&b);
        a=(a+(long long)k*lust-1)%((n+1)>>1)+1,b=(b+(long long)k*lust)%(s+1);
        for(int k=19;~k;k--)if(b<mn[fa[a][k]])a=fa[a][k];
        printf("%d\n",lust=d[a]);
    }
}
int main(){
    scanf("%d",&t);while(t--){
        init();
        build();
        solve();
    }return 0;
}
void init(){clr(vis),clr(d);
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)e[i].clear(),f[i].clear();
    for(int i=0;i<m;i++){
        int a,b,c,d;scanf("%d%d%d%d",&a,&b,&c,&d);
        e[a].pb(b),f[a].pb(c);
        e[b].pb(a),f[b].pb(c);
        ed[i]=(edge){a,b,c,d};
    }sort(ed,ed+m,cmp);
    for(int i=2;i<=n;i++)d[i]=inf;
    q.push((node){0,1});
    while(!q.empty()){
        node nod=q.top();q.pop();
        int v=nod.n;
        if(vis[v])continue;vis[v]=1;
        for(int i=0;i<(int)e[v].size();i++){
            int u=e[v][i],w=d[v]+f[v][i];
            if(!vis[u]&&w<d[u])d[u]=w,q.push((node){w,u});
        }
    }
}