排序算法总结(二)
一、前言
本篇博客属于对排序算法的复习,主要是基于《算法4th》一书。博客正文聚焦的主要是算法的实现过程,对于辅助方法如 less()、exch() 和 isSorted() 等请移步排序算法总结系列导读查看相关实现。
注: 本文中所有的图片均为《算法》一书的辅助图片,代码实现也源自该书。
本文只是对其要点的提炼,想要详细的学习这些算法请自行观看相关书籍。
二、正文
本篇博客将复习的两种排序算法是:
- 归并排序
- 快速排序
1. 归并排序
归并排序是一种基于归并操作的一种排序方式,它的原理如下。
1.1 思想
归并:将两个有序的数组归并成一个更大的有序数组的操作。
归并排序即是将一个数组先递归地分成两半进行排序,然后将结果归并起来,如下图所示。

1.2 代码实现
从归并排序的思想可以看出,其归并操作是整个算法的核心,我们需要定义一个辅助方法 merge(a, lo, mid, hi),它会将子数组 a[lo…mid] 和 a[mid+1…hi] 归并成一个有序的数组并将结果存储在 a[lo…hi] 中。如下所示:
private static void merge(Comparable[] a, int lo, int mid, int hi){
// 将a[lo...mid] 和 a[mid+1...hi]归并
int i = lo, j = mid+1;
// 将a[lo...hi]复制到aux[lo...hi]中
for (int k = lo; k <= hi; k++){
aux[k] = a[k];
}
// 归并回到a[lo...hi]
for (int k = lo; k <= hi; k++){
if (i > mid) a[k] = aux[j++];
else if (j > hi) a[k] = aux[i++];
else if (less(aux[j], aux[i])) a[k] = aux[j++];
else a[k] = aux[i++];
}
}
merge() 方法归并逻辑如下:先将所有元素复制到辅助数组 aux[ ] 中,然后再归并回 a[ ]。归并过程用了4个逻辑判断:
- 左半边的元素用尽时,取右半边的元素;
- 右半边的元素用尽时,取左半边的元素;
- 右半边的当前元素小于左半边的当前元素时,取右半边元素,否则取左半边元素。
实现了归并方法后,我们就可以通过自顶向下的方式,递归调用 merge() 方法来实现归并排序:
public class Merge {
private static Comparable[] aux; // 归并所需的辅助数组
public static void sort(Comparable[] a){
aux = new Comparable[a.length]; // 一次性分配空间
sort(a, 0, a.length - 1);
}
private static void sort(Comparable[] a, int lo, int hi){
// 将数组a[lo...hi]排序
if (lo <= hi) {
return;
}
int mid = lo + (hi - lo)/2;
sort(a, lo, mid); // 对左半部分排序
sort(a, mid+1, hi); // 对右半部分排序
merge(a, lo, mid, hi); // 归并,实现见上面merge()方法代码
}
// less()、exch()和isSorted()方法见本文开头
}
我们以对字符串数组 [ M E R G E S O R T E X A M P L E ] 排序为例展示该代码的运行示意图:
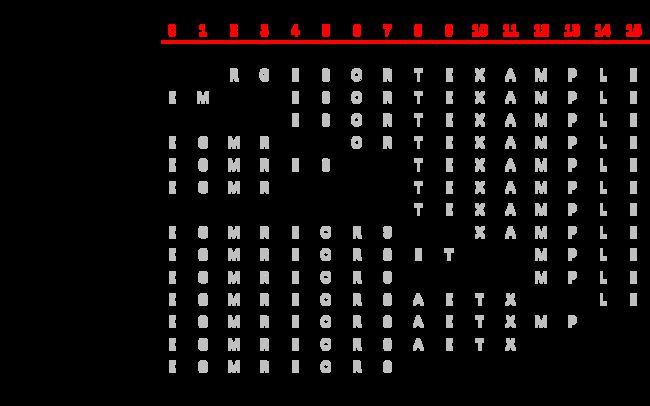
1.3 算法复杂度
对于长度为 N \ N N 的任意数组,自顶向下的递归排序需要 1 / 2 N l g N 至 N l g N \ {1/2}NlgN至NlgN 1/2NlgN至NlgN 次比较。

数组和子数组之间的关系如下图所示:
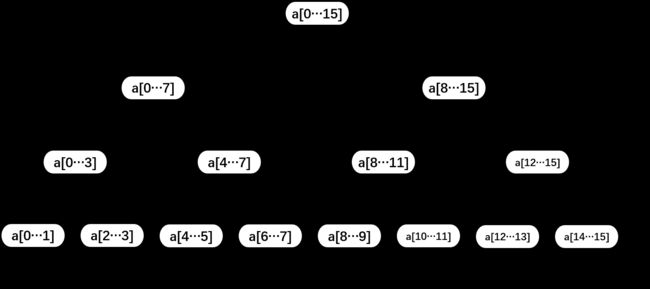
1.4 归并排序的改进
对于归并排序的改进可以从以下三个方面入手:
- 对小规模的数组采用插入排序。插入排序的实现较为简单,因此在处理小数组的插入排序时往往会比归并排序更快,因此我们应当设置一个阈值,当数组大小小于该阈值时就切换为插入排序。
- 测试数组是否已经有序。我们可以增加一个条件,如果 a [ m i d ] ≤ a [ m i d + 1 ] \ a[mid]≤a[mid+1] a[mid]≤a[mid+1],我们就认为数组已经是有序的并跳过
merge()方法。 - 不将元素复制到辅助数组。这点用于节省将元素复制到辅助数组所用的时间,要做到这一点需要调用两种排序方法,一种将数据从输入数组排序到辅助数组,一种将数据从辅助数组排序到输入数组。我们要在递归调用的每个层次交换输入数组和辅助数组的角色。
优化后的归并排序算法代码如下所示:
public class MergeX {
// 切换到插入排序的阈值
private static int THRESHOLD = 8;
public static void sort(Comparable[] a){
Comparable[] aux = a.clone();
sort(aux, a, 0, a.length - 1);
assert isSorted(a);
}
private static void sort(Comparable[] src, Comparable[] dst, int lo, int hi) {
// 当数组长度小于等于8时切换为插入排序
if (hi <= lo + THRESHOLD){
insertionSort(dst, lo, hi);
return;
}
int mid = lo + (hi - lo)/2;
// src和dst轮流作为辅助数组以节省数组的复制时间
sort(dst, src, lo, mid);
sort(dst, src, mid+1, hi);
// 当src[mid+1]不小于src[mid]时,说明此时已经为有序数组,不需进行归并操作
if (!less(src[mid+1], src[mid])){
System.arraycopy(src, lo, dst, lo, hi - lo + 1);
return;
}
// 归并
merge(src, dst, lo, mid, hi);
}
/***************************************************************************
* insertion sort
***************************************************************************/
private static void insertionSort(Comparable[] a, int lo, int hi) {
for (int i = lo+1; i <= hi; i++){
for (int j = i; j > lo && less(a[j], a[j-1]); j--){
exch(a, j, j-1);
}
}
}
private static void merge(Comparable[] src, Comparable[] dst, int lo, int mid, int hi){
assert isSorted(src, lo, mid);
assert isSorted(src, mid+1, hi);
// 将a[lo...mid] 和 a[mid+1...hi]归并
int i = lo, j = mid+1;
for (int k = lo; k <= hi; k++){
if (i > mid) dst[k] = src[j++];
else if (j > hi) dst[k] = src[i++];
else if (less(src[j], src[i])) dst[k] = src[j++];
else dst[k] = src[i++];
}
}
// less()、exch()和isSorted()方法见本文开头
}
做出上述改进之后,在笔者的电脑测试下排序速度提升了约 10%。
2. 快速排序
快速排序是应用最为广泛的排序算法,它的实现较为简单,且在一般应用中比其他排序算法都要快得多。它相比于归并排序最引人注目的特点是它只需要一个很小的辅助栈,而不需要像归并排序一样需要辅助数组。
2.1 思想
快速排序是一种分治的排序算法。它将一个数组切分成两个子数组,将两部分独立地排序,当两个子数组都有序时整个数组也就自然有序了。快速排序中最为重要的一个操作就是切分(partition),切分的位置取决于数组的内容,快速排序的大致过程如下图所示:

2.2 代码实现
快速排序关键在于切分,这个过程使得数组满足下面三个条件:
- 对于某个 j,a[j] 已经排定;
- a[lo] 到 a[j-1] 的所有元素都不大于 a[j];
- a[j+1] 到 a[hi] 的所有元素都不小于 a[j]。
然后我们通过递归地调用切分就可以将数组最终排好序。
所以我们需要先定义一个用于切分的方法,一般策略是先随意地取 a[lo] 作为切分元素,然后从数组的左端开始向右端扫描直到找到一个大于等于它的元素,再从数组的右端向左扫描找到一个小于等于它的元素,交换这两个元素的位置。
如此继续,我们就可以保证左指针 i 的左侧元素都不大于切分元素,右指针 j 的右侧元素都不小于切分元素。当两个指针相遇时,我们只需要将切分元素 a[lo] 和左子数组最右侧的元素(a[j])交换然后返回 j 即可。代码实现如下所示:
private static int partition(Comparable[] a, int lo, int hi){
// 将数组切分成a[lo..i-1], a[i], a[i+1..hi]
int i = lo, j = hi+1; // 左右扫描指针
Comparable v = a[lo]; // 切分元素
while (true){
// 扫描左右,检查扫描是否结束并交换元素
while (less(a[++i], v)) if (i == hi) break;
while (less(v, a[--j])) if (j == lo) break;
if (i >= j) break;
exch(a, i, j);
}
exch(a, lo, j); // 将v = a[j]放入正确位置
return j; // a[lo..j-1] <= a[j] <= a[j+1..hi] 达成
}
我们以对数组 [ K R A T E L E P U I M Q C X O S ] 进行切分为例展示上面切分方法的运行轨迹:

快速排序的实现如下代码所示:
public class Quick {
public static void sort(Comparable[] a){
StdRandom.shuffle(a); // 消除对输入的依赖
sort(a, 0, a.length-1);
assert isSorted(a);
}
private static void sort(Comparable[] a, int lo, int hi){
if (hi <= lo){
return;
}
int j = partition(a, lo, hi);
sort(a, lo, j-1);
sort(a, j+1, hi);
}
// less()、exch()和isSorted()方法见本文开头
}
下面以对数组 [ Q U I C K S O R T E X A M P L E ] 排序为例,展示快速排序实现的运行轨迹图:
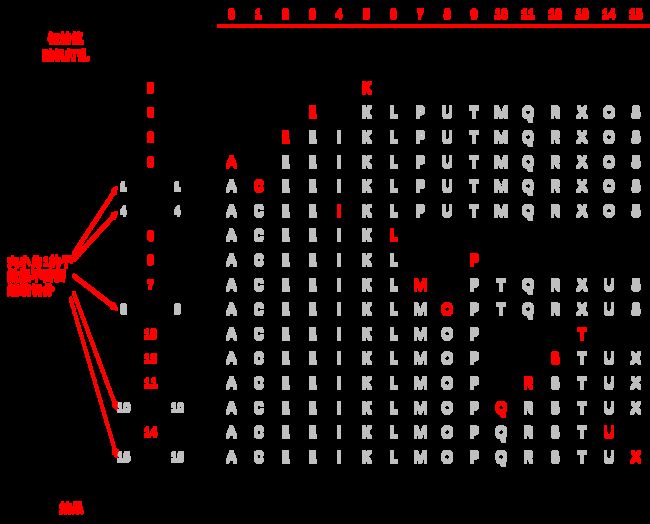
2.3 算法复杂度
快速排序的最好情况是每次都正好能将数组对半分。这种情况下快速排序所用的比较次数正好满足分治递归的 C N = 2 C N / 2 + N \ C{_N}=2C_{N/2}+N CN=2CN/2+N 公式。 2 C N / 2 \ 2C_{N/2} 2CN/2 表示将两个子数组排序的成本, N \ N N 表示用切分元素进行比较的成本。由归并排序的证明可得知 C ( N ) ∼ N l g N \ C(N)\sim NlgN C(N)∼NlgN。但在实际情况中,事情总不会这么顺利,但平均而言切分元素都能落入到数组的中间,所以平均情况下:
将长度为 N \ N N 的无重复数组排序,快速排序平均需要 ∼ 2 N l n N \ \sim 2NlnN ∼2NlnN 次比较(以及 1 / 6 \ 1/6 1/6 的交换)。

尽管平均情况下快速排序的比较次数为 ∼ 2 N l n N \ \sim 2NlnN ∼2NlnN,但是它的基本实现有一个潜在的缺点:在切分不平衡时这个程序可能会极为低效。例如,第一次从最小的元素切分,第二次从第二小的元素切分,如此这般,每次调用只会移除一个元素。这会导致一个大子数组需要切分多次,我们在上述实现中将数组做随机预处理就是为了避免这种情况。
快速排序最多需要约 N 2 / 2 \ N^2/2 N2/2 次比较。
证明。根据上面关于最坏情况的描述,在每次切分后两个子数组之一总是为空的情况下,比较的次数为: N + ( N − 1 ) + ( N − 2 ) + . . . + 2 + 1 = ( N + 1 ) N / 2 \ N+(N-1)+(N-2)+...+2+1=(N+1)N/2 N+(N−1)+(N−2)+...+2+1=(N+1)N/2
2.4 快速排序的改进
对于快速排序的改进可以从以下三个方面入手:
- 切换到插入排序。对于小数组的排序处理,插入排序往往会比快速排序要快,我们只需要像归并排序的改进版本一样设置一个切换的阈值即可。
- 添加哨兵。去掉内循环 while 中的边界检查。由于切分元素本身就是一个哨兵(v不可能小于a[lo]),左侧的边界检查是多余的。要去掉右侧的检查,可以找出数组中的最大值并将其置于数组最右侧即可。在处理内部子数组时,右子数组最左侧元素可以作为左子数组右边界的哨兵。
- 三取样切分。使用子数组的一小部分元素的中位数来切分数组。这样做得到的切分效果更好,但代价是需要计算中位数。人们发现将取样大小设为 3 并用大小居中的元素切分的效果最好。
优化后的快速排序算法代码如下所示:
public class QuickX {
private static final int THRESHOLD = 8;
public static void sort(Comparable[] a){
sort(a, 0, a.length-1);
assert isSorted(a);
}
private static void sort(Comparable[] a, int lo, int hi){
if (hi <= lo){
return;
}
int n = hi - lo + 1;
if (n <= THRESHOLD){
insertionSort(a, lo, hi);
return;
}
int j = partition(a, lo, hi);
sort(a, lo, j-1);
sort(a, j+1, hi);
}
private static int partition(Comparable[] a, int lo, int hi){
int n = hi - lo + 1;
int m = medium3(a, lo, lo+n/2, hi);
exch(a, m, lo);
int i = lo;
int j = hi+1;
Comparable v = a[lo];
// a[lo]等于最大的元素值
while (less(a[++i], v)){
if (i == hi){
exch(a, lo, hi);
return hi;
}
}
// a[lo]等于最小的元素值
while (less(v, a[--j])){
if (j == lo + 1){
return lo;
}
}
// 主循环
while (i < j){
exch(a, i, j);
while (less(a[++i], v));
while (less(v, a[--j]));
}
// 将切分元素v放置到a[j]上
exch(a, lo, j);
return j;
}
private static void insertionSort(Comparable[] a, int lo, int hi) {
for (int i = lo+1; i <= hi; i++){
for (int j = i; j > 0 && less(a[j], a[j-1]); j--){
exch(a, j, j-1);
}
}
}
private static int medium3(Comparable[] a, int i, int j, int k){
return (less(a[i], a[j]) ?
(less(a[j], a[k]) ? j : less(a[i], a[k]) ? k : i) :
(less(a[k], a[j]) ? j : less(a[k], a[i]) ? k : i));
}
// less()、exch()和isSorted()方法见本文开头
}
做出上述改进之后,在笔者的电脑测试下排序速度提升了约 30%。
2.5 非递归的实现方式
递归的代码虽然有助于我们代码上的阅读,但是非递归的实现方式往往会更加好,因为这样可以预防 StackOverflow 异常。
既然是修改成非递归的代码,那么我们就需要思考如何修改。首先我们要添加一个循环来循环地处理各个子数组,并且由于递归本身就是一个栈结构,所以我们会考虑使用一个辅助栈来帮助我们存储相关的信息。那么我们的栈需要存储什么信息呢?
回过头看到 sort() 方法的代码可以发现,我们会重复调用以下代码:
int j = partition(a, lo, hi);
partition() 方法中需要传入参数 lo 和 hi,那么我们就只需要在栈中保留 lo 和 hi 的信息即可,修改后的代码如下所示:
public class QuickXNoRecursive {
......
private static void sort(Comparable[] a, int lo, int hi){
if (hi <= lo){
return;
}
int n = hi - lo + 1;
if (n <= THRESHOLD){
insertionSort(a, lo, hi);
return;
}
Stack<Integer> stack = new Stack<>();
stack.push(lo);
stack.push(hi);
while (!stack.isEmpty()){
hi = stack.pop(); // LIFO,后进先出原则先取 hi
lo = stack.pop(); // LIFO,后进先出原则再取 lo
int j = partition(a, lo, hi);
// 先装进右子数组
if (j+1 < hi) {
if (j + THRESHOLD >= hi) {
// 如果子数组长度小于等于8,改用插入排序
insertionSort(a, j+1, hi);
} else {
// 否则就压入栈中等待切分
stack.push(j+1); // 先压入 lo
stack.push(hi); // 再压入 hi
}
}
// 再装入左子数组
if (lo < j-1){
if (lo + THRESHOLD >= j) {
// 如果子数组长度小于等于8,改用插入排序
insertionSort(a, lo, j-1);
} else {
// 否则就压入栈中等待切分
stack.push(lo); // 先压入 lo
stack.push(j-1); // 再压入 hi
}
}
}
}
......
// 其他未写出代码与 QuickX完全一致
}
三、参考
- 《算法4th》
- 第2章 排序
- 2.2 归并排序
- 2.3 快速排序
- 第2章 排序