SNOI省选模拟赛Round4 T2 最大团clique 二分图（神题）

题目大意：给出n个点的坐标，要求选出最多的点使得这些点两两之间的距离小于等于k。

n<=100。

题解：

这题真是神题啊，我还是太傻了根本没想到这么机智的做法。

爆搜加好的剪枝可以得80分~~

然后说这个机智到不行的做法吧。

首先我们知道一般图的最大团问题是个NPC问题，但这道题的特殊性质可以让我们转成二分图来做。

我们可以先枚举两个点，并且将他们作为最大团中的两个点，显然这两个点的距离首先要满足条件。

然后就是统计含有点i及点j的最大团的顶点数。

重点来了！

怎么快速统计呢？

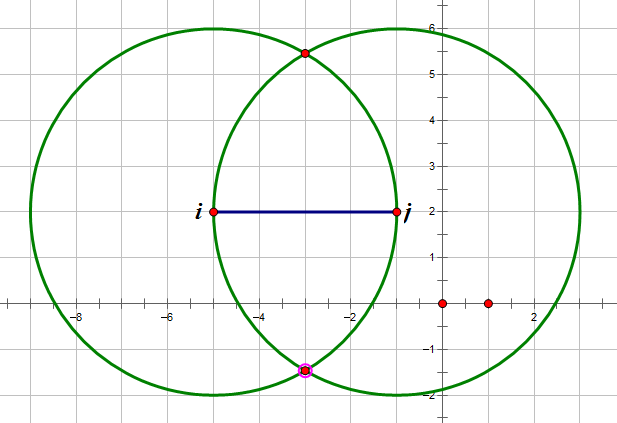
先分别以i，j为圆心，dis(i,j)为半径画圆，如下图。

显然，能在含有(i,j)的最大团里的点只可能在两个圆的重叠部分里。

对于任意在两个圆的重叠部分，且都在线段ij上方的两个点，一定满足条件，都在ij下方同理。

那么难点就是统计跨ij的点对个数。

可以发现：如果跨ij的两个点dis小于等于k，我们可以连一条边，显然不会有两个同上或同下的两个点连边——二分图。

因为二分图的最大团=总点数-其补图的最大匹配数。

于是我们可以据此建二分图的补图，跑最大匹配即可。

注意统计答案时要加2，因为i，j并没有计算在内。

真是太聪明了这个做法，我还得继续学一万年。

代码：

#include
#define maxn 305
using namespace std;
typedef long long LL;
int read()
{
	char c;int sum=0,f=1;c=getchar();
	while(c<'0' || c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0' && c<='9'){sum=sum*10+c-'0';c=getchar();}
	return sum*f;
}
struct point{
	int x,y;
}p[maxn];
point operator -(point a,point b){return (point){a.x-b.x,a.y-b.y};}
int dis(point a){return a.x*a.x+a.y*a.y;}
int det(point a,point b){return a.x*b.y-a.y*b.x;}
int T,n,K,ans;
int match[maxn];
bool can[maxn][maxn],vis[maxn];
int L,R,l[maxn],r[maxn];
bool dfs(int x)
{
	for(int i=1;i<=n;i++)
	{
		if(can[i][x] && !vis[i])
		{
			vis[i]=1;
			if(!match[i] || dfs(match[i]))
			{
				match[i]=x;
				return true;
			}
		}
	}
	return false;
}
int hungry()
{
	int ans=0;
	memset(match,0,sizeof(match));
	for(int i=1;i<=L;i++)
	{
		memset(vis,0,sizeof(vis));
		if(dfs(i))
		ans++;
	}
	return ans;
}
int main()
{
	T=read();
	while(T--)
	{
		ans=0;
		n=read();K=read();
		for(int i=1;i<=n;i++)
		p[i].x=read(),p[i].y=read();
		for(int i=1;i<=n;i++)
		for(int j=i+1;j<=n;j++)
		if(dis(p[i]-p[j])<=K*K)
		{
			L=R=0;
			int d=dis(p[i]-p[j]);
			for(int k=1;k<=n;k++)
			{
				if(k==i || k==j) continue;
				if(dis(p[i]-p[k])<=d && dis(p[j]-p[k])<=d)
				{
					if(det(p[k]-p[i],p[j]-p[i])<=0)
					l[++L]=k;
					else r[++R]=k;
				}
			}
			memset(can,0,sizeof(can));
			for(int i=1;i<=L;i++)
			for(int j=1;j<=R;j++)
			if(dis(p[l[i]]-p[r[j]])>K*K)
			can[i][j]=1;
			int now=L+R-hungry();
			if(now>ans)
			ans=now;
		}
		printf("%d\n",ans+2);
	}
	return 0;
}