分支限界法

分支限界法的基本思想：

1. 求解目标：分支限界法的求解目标则是找出满足约束条件的一个解，或是在满足约束条件的解中找出在某种意义下的最优解。
2. 搜索方式：以广度优先或以最小耗费优先的方式搜索解空间树。分支限界法常以广度优先或以最小耗费（最大效益）优先的方式搜索问题的解空间树。
3. 在分支限界法中，每一个活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点，就一次性产生其所有儿子结点。在这些儿子结点中，导致不可行解或导致非最优解的儿子结点被舍弃，其余儿子结点被加入活结点表中。
4. 此后，从活结点表中取下一结点成为当前扩展结点，并重复上述结点扩展过程。这个过程一直持续到找到所需的解或活结点表为空时为止。

分支限界法示例：

单源最短路径：

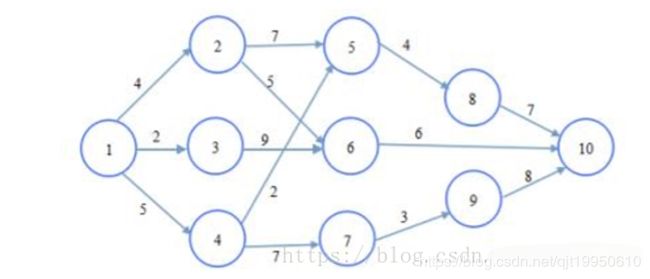
问题：给定一个带权有向图G=（V,E），其中每条边的权是一个实数。另外，还给定V中的一个顶点，称为源。现在要计算从源到其他所有各顶点的最短路径长度。这里的长度就是指路上各边权之和。

分析：

分支限界法的步骤如下：

1)按宽度优先策略遍历解空间树

2)在遍历过程中，对处理的每个结点i，根据界限函数，估计沿该结点向下搜索所可能达到的完全解的目标函数的可能取值范围—界限bound(i)=[dow(i), up(i)]

3) 从中选择使目标函数取的极小值的结点优先进行宽度优先搜索，从而不断调整搜索方向，尽快找到问题解。

在每次分支后，对凡是界限超出已知可行解值那些子集不再做进一步分支。这样，解的许多子集（即搜索树上的许多结点）就可以不予考虑了，从而缩小了搜索范围。

将这个图转化成树的形式，如下所示：

创建队列。 １．节点１入队列，Ｑ＝｛１｝。

我们取出队头节点，作为扩散节点，更新他的后代的值。此题中更新节点２，３，４　的距离，并将他们加入队列，Ｑ＝｛１，２，３，４｝。 完成后节点１出队。Ｑ＝｛２，３，４｝。

２.同样，重复１的步骤，Ｑ＝｛３，４，５，６｝；

３.当我们取到节点３时，我们发现源点－＞节点３－＞节点６的距离为11，大于１－２－６这条路径的权重，所以１－３－６这条路径之后我们不再考虑。 这就是“限界”（称为”剪枝“）的思想。

４.　重复步骤，直到Ｑ为空。优先队列法方法和FIFO方法类似，区别在于优先队列每次取队列元素中到源点距离最短的点。

# Author:Iron
# 初始化图参数 用字典初始初始化这个图
G = {1: { 2: 4, 3: 2,4:5},
     2: { 5: 7, 6: 5},
     3: {6: 9},
     4: {5: 2, 7: 7},
     5: {8: 4},
     6: {10:6},
     7: {9: 3},
     8: {10:7},
     9: {10:8},
     10:{}
    }

inf=9999
#保存源点到各点的距离，为了让顶点和下标一致，前面多了一个inf不用在意。
length=[inf,0,inf,inf,inf,inf,inf,inf,inf,inf,inf]
Q=[]


#FIFO队列实现
def branch(G,v0):
     Q.append(v0)
     dict=G[1]
     while len(Q)!=0:
          #队列头元素出队
          head=Q[0]
          #松弛操作，并且满足条件的后代入队
          for key in dict:
               if length[head]+G[head][key]<=length[key]:
                    length[key]=length[head]+G[head][key]
                    Q.append(key)
         #松弛完毕，队头出列
          del Q[0]
          if len(Q)!=0:
               dict=G[Q[0]]

'''
#优先队列法实现
def branch(G, v0):
     Q.append(v0)
     while len(Q) != 0:
          min=99999
          flag=0
          #找到队列中距离源点最近的点
          for v in Q:
               if min > length[v]:
                    min=length[v]
                    flag = v
          head = flag
          dict=G[head]
          #找到扩散点后进行松弛操作
          for key in dict:
               if length[head] + G[head][key] <= length[key]:
                    length[key] = length[head] + G[head][key]
                    Q.append(key)
          #松弛完毕后，该扩散点出队
          Q.remove(head)
'''

branch(G,1)
print(length)

运行结果：[9999, 0, 4, 2, 5, 7, 9, 12, 11, 15, 15]。