回溯法消消乐

目录

问题描述

一、无剪枝回溯设计

二、剪枝设计

参数准备：

剪枝判断：

三、剪枝设计优缺点分析

缺点：

优点：

四、数据分析

五、剪枝优化：参数可控

六、问题最大规模

七、K、M、N、X分析

K（交换元素的种类）：

M、N（数据规模）：

X（交换步数）：

八、剪枝缺点改进：预测参数

---

问题描述

1、在消消乐中如何计算出最大得分（假设消掉之后不会再补充）

2、分析K（元素种类）、M（棋盘行数）、N（棋盘列数）、X（交换步数）对计算最大得分的方法的影响

一、无剪枝回溯设计

以棋盘状态作为结点，每一个棋盘状态代表一个结点

以最初始的状态为初始结点，以没有可以消除元素的棋盘为叶子结点

先从左下角开始交换，判断是否可以产生新的结点，如果可以产生新的结点，则继续递归从左下角开始交换，继续判断是否可以产生新的结点，直到没有可以消除的元素时，则返回上一个结点，交换下一个位置的元素，继续判断，直到所有棋盘状态都判断过，则终止

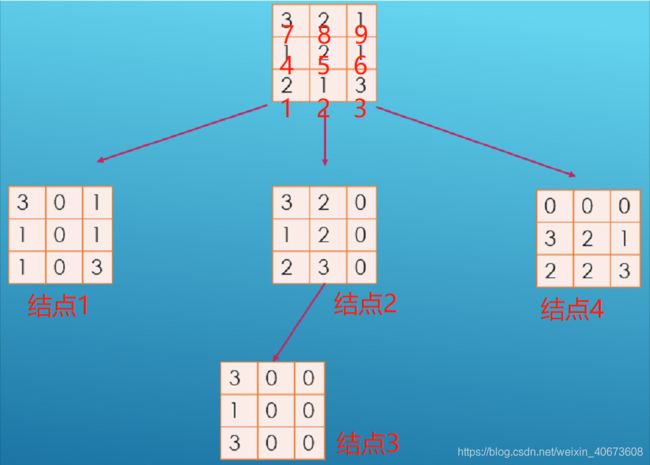
图1

如图1，棋盘初始状态为最初结点

交换位置1和位置2，得到新的棋盘状态，即结点1

结点1没有有效的可交换的元素，返回上一层

交换位置1和4,1和4无法产生新的棋盘状态，跳过

交换位置2和3，产生新的棋盘状态结点2，在结点2中继续交换位置1和2，产生新的棋盘状态结点3

结点3没有有效的可交换元素，返回上一层结点2

结点2没有有效的可交换元素，返回上一层结点1

结点1继续交换位置2和5，得到新的棋盘状态结点4

结点4没有有效的可交换元素，返回上一层结点1

结点1往后都没有有效的可交换元素了，终止

图2

如图2，黄色箭头即为回溯的顺序

二、剪枝设计

参数准备：

在N个测试样本中，用无剪枝回溯计算每个样本的最大得分的平均分a

将无剪枝回溯的递归次数设置为1，计算出N个样本的只交换1步的平均得分b

那么a-b就代表了交换1次后继续交换所能得到的最大平均分

以此类推，可计算出交换1次、2次、3次、4次….. 后继续交换所能得到的最大平均分c1,c2,c3,c4,….cN

剪枝判断：

在新的c1,c2,c3,c4,….cN作为参数

比如说：

在100个随机生成的棋盘样本中，无剪枝回溯得到的平均分是22分，无剪枝回溯只交换1步所得到的平均分是6分，只交换2步所得到的平均分是9分，只交换3步所得到的平均分是11分

则交换1步继续交换下去后可得到的最大平均分是22-6=16分

交换2步继续交换下去后可得到的最大平均分是22-9=13分

交换3步继续交换下去后可得到的最大平均分是22-11=11分

在第k层时先判断当前得分加上此层所对应的参数是否大于当前总分

若大于，代表继续递归仍有较大机会创造出更大的总分，则继续递归

若不大于，代表继续递归能创造出更大的总分的机会比较小，则停止递归，剪掉

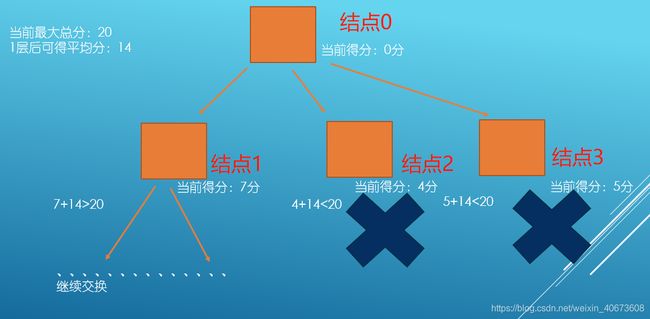
图3

如图3，通过参数准备得到1层后可得的最大平均分是14分

当前最大得分是20分

结点1当前得分是7分，7+14>20,那么保存结点1，继续向下递归

到了结点2的时候，结点2当前得分是4分，4+14<20，则在结点2就停止递归，返回上层继续

到了结点3的时候，同结点2一样情况，剪掉

三、剪枝设计优缺点分析

缺点：

对于每个不同的棋盘都需要用无剪枝回溯法跑多次才可以确定参数，时间开销非常巨大

优点：

参数一旦确定下来，就可以无限复用，对于一款规格大小确定的游戏来说，效果是非常好的

相对于其它预测剪枝，它在运行时可以不用进行相关的预测运算，直接依据参数进行剪枝，节省了预测运算的时间，效率会提升不少

四、数据分析

分差占比=（无剪枝平均得分-剪枝平均得分）/无剪枝平均得分

分差占比反映出准确率，分差占比越大，准确率越低

时间比=无剪枝平均时间/剪枝平均时间

时间比反映出加速了多少倍，时间为2，表示有剪枝速度是相无剪枝速度的2倍

规格	4×5	4×6	4×7	4×8
第1层后可得的最大平均分	5	7	8	14

                                                             表1、不同规格第1层后可得的最大平均得分

	4×5	4×6	4×7	4×8
无剪枝平均得分	9.13	11.52	14.13	21.26
剪枝平均得分	8.70	10.93	12.74	19.12
平均分差	0.43	0.59	1.39	2.14
分差占比	4.7%	5.12%	9.83%	10.06%

                                                               表2、无剪枝回溯和有剪枝回溯的分差占比

	4×5	4×6	4×7	4×8
无剪枝平均时间（ms）	1.88	11.44	46.07	7249.36
剪枝平均时间（ms）	0.77	3.28	5.42	238.73
时间比	2.44	3.48	8.5	30

                                                                 表3、无剪枝回溯和有剪枝回溯的时间比

由表2和表3可以看出，分差占比越小，时间比就越小，分差占比越大，时间比也越大，通俗点总结一下，就是准确度越高，速度越慢，为什么呢？因为剪枝条件越宽松，越容易触发剪枝，速度就越快，但是由于触发的剪枝比较多，所以更有可能错过最佳答案，所以准确度会下降

由此可以得到以下结论：

大部分基于预测的剪枝，包括算期望，算概率，算平均分、贪心预测剪枝等，在速度和准确度上是没法统一的

追求速度，准确度就会下降

追求准确度，速度就会变慢

如果想要在准确度和时间上同时强化，则不能用预测的方法去剪枝

五、剪枝优化：参数可控

基于上面的结论，实际上我们可以不必每次都用计算出来的数作为参数，我们可以根据自己对准确度或者是速度的需求人为地控制参数

参数	分差占比	时间比	备注
5	13.88%	10.02
6	9.02%	5.13
7	5.12%	3.48	无剪枝回溯跑出来的标准参数
8	3.75%	2.511
9	1.61%	1.674
10	0.493%	1.255
11	0.246%	1.18

                                                          表4、4*6规模在不同参数下的分差占比和时间比

如表4，在1000次模拟中，4*6规模的1层后平均最大得分是7分，即参数是7，此参数下的分差占比是5.12%，时间比是3.48

在人为地将参数变小后，分差占比变大，时间比变大

而人为将参数变大后，分差占比变小，时间比变小

所以，此剪枝方法是非常灵活的，我们可以根据自己对准确度或者是速度的需求人为地控制参数，间接控制我们想要的分差比和速度比

六、问题最大规模

由于剪枝方法的参数是基于无剪枝回溯法得出的，所以它可求解的最大规模就是无剪枝回溯法的最大规模

七、K、M、N、X分析

K（交换元素的种类）：

对于K，当K变大甚至超过一定数量时，得分会陡降

因为K越大，同一规模下所能消掉的分就越少

当K大到一定的时候，会导致3个连在一起的情况非常少

所以得分在那时就会陡降

M、N（数据规模）：

M、N越大，那么在参数不变的前提下，所剪掉的枝的层数就会越大，这样的话，速度可以得到极大提升，但是，由于剪掉的枝的范围变得更大了，所以更有几率剪掉最优的解，所以准确度会下降

此外，由于参数可调这种灵活性，在M、N增大时，可以人为地把参数调大一些，补救一下因M、N变大而带来的准确率降低的问题

X（交换步数）：

对于此方法，X当然是越小越好

因为此方法基于无剪枝回溯法

X越小，无剪枝回溯法越容易得到最终平均分，即越容易得到参数

八、剪枝缺点改进：预测参数

上面的剪枝方法的最大缺点，就是它的参数必须由无剪枝回溯法得出，这大大降低了它在规模大的时候的可行性，所以可以做以下的改进，把缺点抹掉

由于棋盘规模变大，1次交换更容易出现几连消的情况，此外，最大得分也受棋盘规模的影响，所以上面的剪枝方法中的参数是和棋盘规模有关系的

那么我们就可以计算出小规模时的参数，通过多项式方程拟合，拟合出大规模时的表达式

这样，我们就可以直接根据低规模时的参数直接预测出大规模时的参数，从而绕开剪枝回溯法，增加此剪枝方法的可行性

你可能会怀疑拟合方程在拟合大规模参数时可能出现大误差！但是，由于参数可控这个灵活性，所谓的大规模参数大误差，只不过是参数可控表里的某个参数的情况，它所代表的只不过是准确度较低或者速度较慢这2种极端情况

在此情况下，我们仍然可以人为地根据拟合出来的大规模参数进行调整，根据实际情况把参数适当调大或者调小，进而把极端情况改良，避免大误差